Abstract
In this paper, we face the serious problem of food health hazard, also in connection with global food production scarcity and feeding sustainability, in view of important environmental issues and the severe incumbent climate change. Specifically, our innovative risk management approach considers cooperation among producers of vegan and non-vegan food, a strong commitment more and more observed, recently, in technologically advanced western countries. The novelty of our work consists in proposing possible quantitative agreements among complementary food producers, usually non-interacting, in order to develop a sustainable healthy food production for human population—also characterized by low impact on the planet. Another new feature of our approach lies in using coopetition and game theory together; we show, quantitatively, how to conjugate human health defense, environmental defense, economic interests and less government spending, needs which usually appear in contrast with each other. Another point of our coopetitive approach is the suggestion of an easier way to entry the global market for vegan food producers. Meanwhile, our model suggests to big producers/sellers of non-vegan food a way to smoothly and rapidly transit toward more sustainable production. Technically, we propose an innovative exemplary complex agreement among global food sellers and small (but strongly sustainable and innovative) vegan food producers. Moreover, our model implies a general saving for the countries, by mitigating the health expenditures. The result of our mathematical study suggests a novel win–win solution for global economy, world environment and governments, while improving human population sustainability and climate change effects.




Similar content being viewed by others
Notes
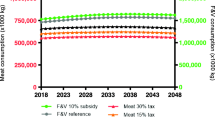
The parameters of the model come from telephone interviews at local McDonald’s and Muscle of Wheat employees about the selling price of possible vegan and vegetarian complete menu in McDonald’s and production costs and selling price of some convenient vegan-burger produced by Muscle of Wheat. We obtained an average price of 7 $ in the market (\(p_{10}\)) for any menu containing vegan-burger, while one vegan-burger (without bread or any other side dishes) costs to McDonald’s 1 $ for each bought from third player (\(p_{31}\)). For what concerns Muscle of Wheat, the selling price of one vegan-burger to the market is 5 $ (\(p_{20}\)), while the fixed cost F is 20 million $ for one year of production with a forecasted maximum production of 160 million pieces in a year.
References
Baglieri D, Carfì D, Dagnino G (2012) Asymmetric R&D alliances and coopetitive games. In: Advances in computational intelligence, communications in computer and information science, vol 300. Springer, Berlin, pp 607–621. https://doi.org/10.1007/978-3-642-31724-8_64
Baglieri D, Carfì D, Dagnino GB (2016) Asymmetric R&D alliances in the biopharmaceutical industry. Int Stud Manag Organ 46(2(3)):179–201. https://doi.org/10.1080/00208825.2016.1112154
Baumert KA, Herzog T, Pershing J, Institute WR (2005) Navigating the numbers: greenhouse gas data and international climate policy. World Resources Institute, Washington, D.C
Carfì D, Donato A (2018) Coopetitive games for sustainability of global feeding and climate change: recent developments. J Environ Manag Tour 9(1(25)):200–215. https://doi.org/10.14505//jemt.v9.1(25).25
Carfì D, Donato A, Panuccio D (2017) A game theory coopetitive perspective for sustainability of global feeding: agreements among vegan and non-vegan food firms. In: Sustainable entrepreneurship and investments in the green economy, book series on advances in business strategy and competitive advantage (ABSCA). IGI Global, pp 100–143. https://doi.org/10.4018/978-1-5225-2075-7.ch004
Carfì D, Donato A, Schilirò D (2018) Sustainability of global feeding. Coopetitive interaction among vegan and non-vegan food firms. In: Book of papers of 24th international sustainable development research society conference “action for a sustainable world: from theory to practice”, pp 592–605
Carfì D, Donato A, Schilirò D (2019) Coopetitive solutions of environmental agreements for the global economy after COP21 in Paris. J Environ Manag. https://doi.org/10.1016/j.jenvman.2019.109331
Carfì D, Romeo A (2015) Improving welfare in Congo: Italian national hydrocarbons authority strategies and its possible coopetitive alliances with green energy producers. J Appl Econ Sci 10(4 (34)):571–592
Carfì D, Schilirò D (2012a) A coopetitive model for the green economy. Econ Model 29(4):12151–219. https://doi.org/10.1016/j.econmod.2012.04.005
Carfì D, Schilirò D (2012b) Global green economy and environmental sustainability: a coopetitive model. In: Advances in computational intelligence, communications in computer and information science, vol 300. Springer, Berlin, pp 593–606. https://doi.org/10.1007/978-3-642-31724-8_63
Deng W, Zhao H, Yang X, Xiong J, Sun M, Li B (2017a) Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment. J Appl Soft Comput 59(C):288–302. https://doi.org/10.1016/j.asoc.2017.06.004
Deng W, Zhao H, Zou L, Yang X, Wu D (2017b) A novel collaborative optimization algorithm in solving complex optimization problems. Soft Comput 21(15):4387–4398. https://doi.org/10.1007/s00500-016-2071-8
Deng W, Xu J, Zhao H (2019) An improved ant colony optimization algorithm based on hybrid strategies for scheduling problem. IEEE Access 7:20281–20292. https://doi.org/10.1109/ACCESS.2019.2897580
Fiala N (2008) Meeting the demand: an estimation of potential future greenhouse gas emissions from meat production. Ecol Econ 67(3):412–419
Fields H et al (2016) Is meat killing us? J Am Osteopath Assoc 116:296–300. https://doi.org/10.7556/jaoa.2016.059
Foley JA et al (2011) Solutions for a cultivated planet. Nature 478(7369):337–342
Kompas T, Pham VH, Che TN (2018) The effects of climate change on GDP by country and the global economic gains from complying with the Paris climate accord. Earth’s Future 6(8):1153–1173. https://doi.org/10.1029/2018EF000922
OECD (2019) Health status: cancer. https://stats.oecd.org/. Accessed May 2019
OECD-FAO (2019a) Agricultural outlook 2011–2020. Cereals consumption: kilograms/capita. https://stats.oecd.org/. Accessed May 2019
OECD-FAO (2019b) Agricultural outlook 2011–2020. Meat consumption (beef and veal): kilograms/capita. https://stats.oecd.org/ . Accessed May 2019
Saint Louis C (2015) Meat and cancer: the W.H.O. report and what you need to know. The New York Times. Retrieved online at https://www.nytimes.com/interactive/2015/10/26/health/meat-cancer-who-report.html
Tuomisto HL, Teixeira DMMJ (2011) Environmental impacts of cultured meat production. Environ Sci Technol 45(14):6117–6123
Walker P, Rhubart-Berg P, Mckenzie S, Kelling K, Lawrencw R (2005) Public health implications of meat production and consumption. Public Health Nutr 8(4):348–356
WHO (2015) Q&A on the carcinogenicity of the consumption of red meat and processed meat. http://www.who.int/features/qa/cancer-red-meat/en/. Accessed May 2019
Zhao H, Sun M, Deng W, Yang X (2017) A new feature extraction method based on EEMD and multi-scale fuzzy entropy for motor bearing. Entropy. https://doi.org/10.3390/e19010014
Zhao H, Yao R, Xu L, Yuan Y, Li G, Deng W (2018) Study on a novel fault damage degree identification method using high-order differential mathematical morphology gradient spectrum entropy. Entropy. https://doi.org/10.3390/e20090682
Zhao H, Zheng J, Xu J, Deng W (2019) Fault diagnosis method based on principal component analysis and broad learning system. IEEE Access 7:99263–99272. https://doi.org/10.1109/ACCESS.2019.2929094
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by M. Squillante.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: complete analysis of the parametric game
Appendix: complete analysis of the parametric game
In this appendix, we study the parametric game
associated with the game G.
1.1 Preliminaries
We now consider the parametric game \({\mathcal {G}} = (p, >)\) associated with the coopetitive game \(G= (f,>).\) Note that, fixed a cooperative strategy \(z_1\) in the interval \({\mathcal {C}}_1\), the parametric game defined by
with parametric payoff function
defined on the parallelepiped \(T_2\) (cartesian product of \({\mathcal {E}}\), \({\mathcal {F}}\) and \({\mathcal {C}}_2\)) by
is the translation of the game \({\mathcal {G}}(0)\) by the infinite family of vectors defined by
So that we can study the game \({\mathcal {G}}(0)\) and then we can translate the various information of the game \({\mathcal {G}}(0)\) by the infinite family of vectors \(w_1(z_1)\).
More specifically, we fix the intervals of the strategy space and the other constant of the game as follows.Footnote 1
For our convenience, in the representation of payoff space, we consider a game translated by the vector \((-3.6,0)\), so that to the payoff of the first player we need to add, at the end of the day, exactly 3.6 equal 144 million dollars.
From (4), we have:
We define the new parametric game
by
for every
where
Observe that
for every \((x,y)\in {\mathcal {E}}\times {\mathcal {F}}\).
The image of the function
is the union
The function
is defined by
Now, we immediately see that
Since
for every \(z_1 \in {\mathcal {C}}_1\), then
So, let us consider the game \({\mathcal {G}}(0)=(H,>)\) and let
defined by
the function such that
In order to graph the payoff space
we transform all the vertices of the bi-strategy square Q by the function \(H(.,z_2)\).
In particular, we have
where
1.2 Payoff space of game \((g,>)\)
The transformation of segment [A, B] by means of the function g is the segment
where
is the payoff (− 5.5, 0) and
is the payoff (0.5, 0).
The transformation of segment [B, C] by means of the function g is the segment
where
The transformation of segment [C, D] by means of the function g is the segment
where
is the payoff (− 7, 0.5).
The transformation of segment [A, D] by means of the function g is the segment
In Fig. 5, we show the payoff space g(Q).
1.3 Payoff space of game \({(H(.,z_2),>)}\)
We now consider the payoff section
defined by
for every \((x,y) \in {\mathcal {E}}\times {\mathcal {F}}\), with \(z_2 \in {\mathcal {C}}_2\).
The transformation of segment [A, B] by means of the function \({H(.,z_2)}\) is the segment
where
is the payoff
and
is the payoff
The transformation of segment [B, C] by means of the function \({H(.,z_2)}\) is the segment
where
is the payoff
The transformation of segment [C, D] by means of the function \({H(.,z_2)}\) is the segment
where
is the payoff
The transformation of segment [A, D] by means of the function \({H(.,z_2)}\) is the segment
In Fig. 6, we show the payoff space \(H(T_2)\).
We see in Fig. 6 the moving segment
This segment \([B',C']\) comes from the transformation of the segment [B, C], which shows the first coordinate of all its points equal to one. The segment \([B',C']\) is moving progressively toward the left, as the strategy \(z_2\) increases. We observe that the moving segment \([A',D']\), coming from [A, D], lies always at the left of the moving segment \([B',C']\), until the value of the strategy \(z_2\) reaches the level 12/7.
Remark
Observe that, we have defined four parametric curves in the Cartesian plane, namely the four curves \(A'\), \(B'\), \(C'\) and \(D'\). These four curves are defined on the compact interval [0, 4] even if, for our coopetitive analysis, we consider only the parts of curves with endpoints corresponding to the values 1 and 4 of the coopetitive parameter z.
1.4 Payoff space of the coopetitive game G
Now, we consider the translation of the game \(H(., .,z_2)\) by the vector
with \(z_1 \in [1,2]\), in order to obtain the total payoff space of the coopetitive game (see Fig. 7).
The final payoff space of our coopetitive game is the union
We show in Fig. 8 the filled payoff space of the game G.
1.5 The Pareto maximal boundary of the payoff space f(S)
The Pareto maximal boundary of the payoff space f(S) of the coopetitive game G, where S denotes the strategy space of the game Cartesian product of the strategy square Q and of the intervals \({\mathcal {C}}_1\) and \({\mathcal {C}}_2\), is the union of the segments
where the point
In Fig. 9, we see the Pareto maximal boundary of the payoff space.
1.6 Study of the Nash zone
Recalling the payoff function of the game defined by (5) for every \((x,y,z) \in S\). The Nash equilibrium strategies of the first player are determined solving the optimum problem
for every \(z \in {\mathcal {C}}\) and \({y} \in {\mathcal {F}}\). The Nash strategy set of the first player \(N_1(z)\) is the set of the solutions of the optimization problem.
The Nash equilibrium strategies of the second player are determined solving the optimum problem
for every \(z \in {\mathcal {C}}\) and \({x} \in {\mathcal {E}}\). The Nash strategy set of the first player \(N_1(z)\) is the set of the solutions of the first optimization problem.
Let us consider the positiveness of the first argument derivative of \(f_1\) (with \(x \in [0,1]\)). From that we obtain
that gives
The second argument derivative of \(f_2\),
results positive for every \((x,y,z) \in S\), so the Nash strategy for the second player (with \(y \in [1,2]\)) is 2. So, the multivalued coopetitive Nash path is
for every \(z \in {\mathcal {C}}\). From that we calculate the Nash zone in the payoff space (see Fig. 10).
Rights and permissions
About this article
Cite this article
Carfí, D., Donato, A. Risk management of food health hazard by meat consumption reduction: a coopetitive game approach. Soft Comput 24, 13705–13716 (2020). https://doi.org/10.1007/s00500-019-04474-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-019-04474-6