Optimal operational strategies of capital-constrained supply chain with logistics service and price dependent demand under 3PL financing service

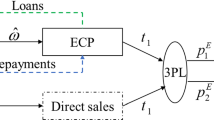
Abstract

In a supply chain finance (SCF) system composed of a manufacturer, a retailer and a third-party logistics (3PL) enterprise, the market demand is dependent on the logistics service level and the retail price. This paper investigates the optimal operational strategies for the SCF system with the 3PL financing service when the retailer or the manufacturer is stuck with capital constraint, respectively. By constructing and solving Stackelberg game models, we obtain the optimal operational strategies of the above two scenarios, and combined with the sensitivity analysis of relevant parameters, we obtain the following conclusions. (1) For the SCF system with a capital-constrained retailer, except the manufacturer’s optimal wholesale price remains unchanged, other participants’ optimal decisions and the optimal profits of each participant increase with the logistics service sensitivity coefficient; except the manufacturer’s optimal wholesale price remains unchanged, other participants’ optimal decisions and the optimal profits of each participant decrease with the logistics service cost efficiency. (2) For the SCF system with a capital-constrained manufacturer, the optimal decisions and profits of supply chain participants increase with the logistics service sensitivity coefficient; the optimal decisions and profits of supply chain participants decrease with the logistics service cost efficiency. Our analysis suggests that the retailer and manufacturer must take into account 3PL enterprise’s decisions (logistics service level and logistics service price) under the 3PL financing service mode before making decisions.

Appendix

Proof of Proposition 1

Taking the first-order and the second-order derivative of $\pi_{\text{r}}$ w.r.t. p in Eq. (1), we have

$$ \frac{{{\text{d}}\pi_{\text{r}} }}{{{\text{d}}p}} = bi_{\text{r}} w - bp - b\left( { - l + p - w} \right) + d + \theta \zeta $$

(A.1)

$$ \frac{{{\text{d}}^{2} \pi_{\text{r}} }}{{{\text{d}}p^{2} }} = - 2b $$

(A.2)

where $Q = d - bp + \theta \zeta$.

From Eq. (A.2), we have $\frac{{{\text{d}}^{2} \pi_{\text{r}} }}{{{\text{d}}p^{2} }} = - 2b < 0$, which means that the retailer’s profit function is concave and that there exists a unique $p^{ * }$. From the first-order condition, i.e., $\frac{{{\text{d}}\pi_{\text{r}} }}{{{\text{d}}p}} = 0$, we can obtain the retailer’s optimal retail price, i.e., $p^{ * } = \frac{1}{2b}\left[ {b\left( {i_{\text{r}} w + l + w} \right) + d + \theta \zeta } \right]$. Then, substituting $p^{ * }$ in $Q = d - bp^{ * } + \theta \zeta$, we have $Q^{*} = - \frac{b}{2}\left( {i_{\text{r}} w + l + w} \right) + \frac{d}{2} + \frac{\theta \zeta }{2}$.

Proof of Corollary 1

Differentiating the optimal retail price $p^{ * }$ w.r.t. w, we have $\frac{{{\text{d}}p^{ * } }}{{{\text{d}}w}} = \frac{{i_{\text{r}} }}{2} + \frac{1}{2}$. Since $i_{\text{r}} > 0$ in Table 1, we can obtain $\frac{{dp^{ * } }}{dw} = \frac{{i_{r} }}{2} + \frac{1}{2} > 0$. Furthermore, differentiating the optimal order quantity $Q^{ * }$ w.r.t. w, we have $\frac{{{\text{d}}Q^{ * } }}{{{\text{d}}w}} = - \frac{b}{2}\left( {i_{\text{r}} + 1} \right)$. Since $b,i_{\text{r}} > 0$, we can derive $\frac{{{\text{d}}Q^{ * } }}{{{\text{d}}w}} = - \frac{b}{2}\left( {i_{\text{r}} + 1} \right) < 0$.

Proof of Corollary 2

Differentiating the optimal retail price $p^{ * }$ w.r.t. the financing interest rate i_r, we have $\frac{{{\text{d}}p^{ * } }}{{{\text{d}}i_{\text{r}} }} = \frac{w}{2}$. Since $w > 0$, we can obtain $\frac{{{\text{d}}p^{ * } }}{{{\text{d}}i_{\text{r}} }} = \frac{w}{2} > 0$. Furthermore, differentiating the optimal order quantity $Q^{ * }$ w.r.t. the financing interest rate i_r, we have $\frac{{{\text{d}}Q^{ * } }}{{{\text{d}}i_{\text{r}} }} = - \frac{bw}{2}$. Since $b,w > 0$, we can derive $\frac{{{\text{d}}Q^{ * } }}{{{\text{d}}i_{\text{r}} }} = - \frac{bw}{2} < 0$.

Proof of Corollary 3

Differentiating the optimal retail price $p^{ * }$ and the optimal order quantity $Q^{ * }$ w.r.t. the price sensitivity coefficient b, we have $\frac{{ {\text{d}}p^{ * } }}{ {{\text{d}}b}} =\frac{1}{2b}\left( {i_{\text{r}} w + l + w} \right) - \frac{1}{{2b^{2} }}\left[ {b\left( {i_{\text{r}} w + l +w} \right) + d + \theta \zeta } \right]$ and $\frac{{{\text{d}}Q^{ * } }}{{{\text{d}}b}} = - \frac{{i_{\text{r}} w}}{2} - \frac{l}{2} - \frac{w}{2}$. Since $b,w,d,i_{\text{r}} ,\theta ,\zeta ,l > 0$, we can obtain $\frac{{ {\text{d}}p^{ * } }}{ {{\text{d}}b}} =\frac{1}{2b}\left( {i_{\text{r}} w + l + w} \right) - \frac{1}{{2b^{2} }}\left[ {b\left( {i_{\text{r}} w + l +w} \right) + d + \theta \zeta } \right] < 0$ and $\frac{{{\text{d}}Q^{ * } }}{{{\text{d}}b}} = - \frac{{i_{\text{r}} w}}{2} - \frac{l}{2} - \frac{w}{2} < 0$.

Proof of Proposition 2

Taking the first-order derivative of $\pi_{{3{\text{PL}}}}$ w.r.t. $\zeta$ and l in Eq. (2) respectively, we have

$$ \frac{{{\text{d}}\pi_{{3{\text{PL}}}} }}{{{\text{d}}\zeta }} = - \eta \zeta + \frac{{i_{\text{r}} \theta }}{2}w - \frac{\theta }{2}\left( {c_{l} - l} \right) $$

(A.3)

$$ \frac{{{\text{d}}\pi_{{3{\text{PL}}}} }}{{{\text{d}}l}} = - \frac{{bi_{\text{r}} }}{2}w + \frac{b}{2}\left( {c_{l} - l} \right) - \frac{b}{2}\left( {i_{\text{r}} w + l + w} \right) + \frac{d}{2} + \frac{\theta \zeta }{2} $$

(A.4)

Differentiating Eqs. (A.3) and (A.4) w.r.t. $\zeta$ and l, respectively, we can derive the Hessian Matrix as follows:

$$ H\left( {\zeta ,l} \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{{\partial \zeta^{2} }}} & {\frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{\partial \zeta \partial l}} \\ {\frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{\partial l\partial \zeta }} & {\frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{{\partial l^{2} }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \eta } & {\frac{\theta }{2}} \\ {\frac{\theta }{2}} & { - b} \\ \end{array} } \right] $$

(A.5)

From Eq. (A.5), the first-order sequential principal minor of the Hessian Matrix $\left| {H_{1} \left( {\zeta ,l} \right)} \right| = \frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{{\partial \zeta^{2} }} = - \eta < 0$ and the second-order sequential principal minor of the Hessian Matrix $\left| {H_{2} \left( {\zeta ,l} \right)} \right| = \frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{{\partial \zeta^{2} }} \times \frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{{\partial l^{2} }} - \frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{\partial \zeta \partial l} \times \frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{\partial l\partial \zeta } = - \eta \times \left( { - b} \right) - \frac{\theta }{2} \times \frac{\theta }{2} = b\eta - \frac{{\theta^{2} }}{4} > 0$, i.e., the Hessian Matrix is negative definite. Therefore $\pi_{{3{\text{PL}}}}$ is concave w.r.t. $\left( {\zeta ,l} \right)$, and there exists a unique optimal solution, respectively. From the first-order condition, i.e., $\frac{{{\text{d}}\pi_{{3{\text{PL}}}} }}{{{\text{d}}\zeta }} = 0$ and $\frac{{{\text{d}}\pi_{{3{\text{PL}}}} }}{{{\text{d}}l}} = 0$, we can obtain the 3PL enterprise’s optimal logistics service level $\zeta^{ * }$ and the optimal logistics service price $l^{ * }$, i.e., $\zeta^{ * } { = } - \frac{{\theta \left( {bc_{l} + bw - d} \right)}}{{4b\eta - \theta^{2} }}$ and $l^{ * } = \frac{1}{{4b\eta - \theta^{2} }}\left[ {2\eta \left( {bc_{l} - 2bi_{\text{r}} w - bw + d} \right) - \theta^{2} \left( {c_{l} - i_{\text{r}} w} \right)} \right]$.

Proof of Proposition 3

Taking the first-order and the second-order derivative of $\pi_{\text{m}}$ w.r.t. w in Eq. (3), we have

$$ \frac{{{\text{d}}\pi_{\text{m}} }}{{{\text{d}}w}} = \frac{b\eta }{{16b\eta - 4\theta^{2} }}\left( {4bc - 4bc_{l} - 8bw + 4d} \right) $$

(A.6)

$$ \frac{{{\text{d}}^{2} \pi_{\text{m}} }}{{{\text{d}}w^{2} }} = - \frac{{8b^{2} \eta }}{{16b\eta - 4\theta^{2} }} $$

(A.7)

From Eq. (A.7), we have $\frac{{{\text{d}}^{2} \pi_{\text{m}} }}{{{\text{d}}w^{2} }} = - \frac{{8b^{2} \eta }}{{16b\eta - 4\theta^{2} }} < 0$, which means that the manufacturer’s profit function is concave and that there exists a unique $w^{ * }$. From the first-order condition, i.e., $\frac{{{\text{d}}\pi_{\text{m}} }}{{{\text{d}}w}} = 0$, we can obtain the manufacturer’s optimal wholesale price, i.e., $w^{ * } = \frac{1}{2b}\left( {bc - bc_{l} + d} \right)$.

Proof of Proposition 4

Taking the first-order and the second-order derivative of $\pi_{\text{r}}$ w.r.t. p in Eq. (4), we have

$$ \frac{{{\text{d}}\pi_{\text{r}} }}{{{\text{d}}p}} = - bp - b\left( {p - w} \right) + d + \theta \zeta $$

(A.8)

$$ \frac{{{\text{d}}^{2} \pi_{\text{r}} }}{{{\text{d}}p^{2} }} = - 2b $$

(A.9)

where $Q = d - bp + \theta \zeta$.

From Eq. (A.9), we have $\frac{{{\text{d}}^{2} \pi_{\text{r}} }}{{{\text{d}}p^{2} }} = - 2b < 0$, which means that the retailer’s profit function is concave and that there exists a unique $p^{ * }$. From the first-order condition, i.e., $\frac{{{\text{d}}\pi_{\text{r}} }}{{{\text{d}}p}} = 0$, we can obtain the retailer’s optimal retail price, i.e., $p^{ * } = \frac{1}{2b}\left( {bw + d + \theta \zeta } \right)$. Then, substituting $p^{ * }$ in $Q = d - bp^{ * } + \theta \zeta$, we have $Q^{*} { = } - \frac{bw}{2} + \frac{d}{2} + \frac{\theta \zeta }{2}$.

Proof of Proposition 5

Taking the first-order and the second-order derivative of $\pi_{\text{m}}$ w.r.t. w in Eq. (5), we have

$$ \frac{{{\text{d}}\pi_{\text{m}} }}{{{\text{d}}w}} = \frac{bc}{2}i_{\text{m}} + \frac{bl}{2} - \frac{bw}{2} + \frac{b}{2}\left( {c - w} \right) + \frac{d}{2} + \frac{\theta \zeta }{2} $$

(A.10)

$$ \frac{{{\text{d}}^{2} \pi_{\text{m}} }}{{{\text{d}}w^{2} }} = - b $$

(A.11)

From Eq. (A.11), we have $\frac{{{\text{d}}^{2} \pi_{\text{m}} }}{{{\text{d}}w^{2} }} = - b < 0$, which means that the manufacturer’s profit function is concave and that there exists a unique $w^{ * }$. From the first-order condition, i.e., $\frac{{{\text{d}}\pi_{\text{m}} }}{{{\text{d}}w}} = 0$, we can obtain the manufacturer’s optimal wholesale price, i.e., $w^{ * } = \frac{1}{2b}\left( {bci_{\text{m}} + bc + bl + d + \theta \zeta } \right)$.

Proof of Proposition 6

Taking the first-order derivative of $\pi_{{3{\text{PL}}}}$ w.r.t. $\zeta$ and l in Eq. (6), respectively, we have

$$ \frac{{{\text{d}}\pi_{{3{\text{PL}}}} }}{{{\text{d}}\zeta }} = \frac{{ci_{\text{m}} }}{4}\theta - \eta \zeta - \frac{\theta }{4}\left( {c_{l} - l} \right) $$

(A.12)

$$ \frac{{{\text{d}}\pi_{{3{\text{PL}}}} }}{{{\text{d}}l}} = - \frac{bc}{2}i_{\text{m}} - \frac{bc}{4} - \frac{bl}{4} + \frac{b}{4}\left( {c_{l} - l} \right) + \frac{d}{4} + \frac{\theta \zeta }{4} $$

(A.13)

Differentiating Eqs. (A.12) and (A.13) w.r.t. $\zeta$ and l, respectively, we can derive the Hessian Matrix as follows:

$$ H\left( {\zeta ,l} \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{{\partial \zeta^{2} }}} & {\frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{\partial \zeta \partial l}} \\ {\frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{\partial l\partial \zeta }} & {\frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{{\partial l^{2} }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \eta } & {\frac{\theta }{4}} \\ {\frac{\theta }{4}} & { - \frac{b}{2}} \\ \end{array} } \right] $$

(A.14)

From Eq. (A.14), the first-order sequential principal minor of the Hessian Matrix $\left| {H_{1} \left( {\zeta ,l} \right)} \right| = \frac{{\partial^{2} \pi_{3PL} }}{{\partial \zeta^{2} }} = - \eta < 0$ and the second-order sequential principal minor of the Hessian Matrix $\left| {H_{2} \left( {\zeta ,l} \right)} \right| = \frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{{\partial \zeta^{2} }} \times \frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{{\partial l^{2} }} - \frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{\partial \zeta \partial l} \times \frac{{\partial^{2} \pi_{{3{\text{PL}}}} }}{\partial l\partial \zeta } = - \eta \times \left( { - \frac{b}{2}} \right) - \frac{\theta }{4} \times \frac{\theta }{4} = \frac{1}{2}b\eta - \frac{{\theta^{2} }}{16} > 0$, i.e., the Hessian Matrix is negative definite. Therefore $\pi_{{3{\text{PL}}}}$ is concave w.r.t. $\left( {\zeta ,l} \right)$, and there exists a unique optimal solution, respectively. From the first-order condition, i.e., $\frac{{{\text{d}}\pi_{{3{\text{PL}}}} }}{{{\text{d}}\zeta }} = 0$ and $\frac{{{\text{d}}\pi_{{3{\text{PL}}}} }}{{{\text{d}}l}} = 0$, we can obtain the 3PL enterprise’s optimal logistics service level $\zeta^{ * }$ and the optimal logistics service price $l^{ * }$, i.e., $\zeta^{ * } { = } - \frac{{\theta \left( {bc + bc_{l} - d} \right)}}{{8b\eta - \theta^{2} }}$ and $l^{ * } = \frac{1}{{8b\eta - \theta^{2} }}\left[ { - 4\eta \left( {2bci_{\text{m}} + bc - bc_{l} - d} \right) + \theta^{2} \left( {ci_{\text{m}} - c_{l} } \right)} \right]$.