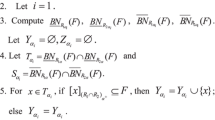Abstract
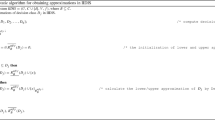
The incremental learning methods based on rough set theory are effective in acquiring knowledge in dynamically changing information tables. In this paper, we focus on the effective acquisition of decision rules by incrementally updating approximations when an incomplete information table changes. First of all, we present a four-step model to obtain three-way decision rules in an incomplete information table based on the graded tolerance relation. The first step presents the graded tolerance relation between objects. The second step calculates the degrees of objects belonging to approximations by using fuzzy logic operators. Besides, we propose a relation matrix to calculate the degrees efficiently. The third step gets three-way approximations by applying a pair of thresholds to the degrees. The fourth step obtains three-way decision rules based on the descriptions of objects. According to the four-step model, we find the notion of approximations plays an essential role in rule acquisition. Incrementally updating approximations are an effective method to obtain decision rules when an incomplete information changes. Accordingly, we study the incrementally updating approximations by incrementally updating the relation matrix when changing attributes, objects, and the attribute value of an object. Finally, experimental results illustrate that the incremental methods are more effective than non-incremental methods.








Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Baczyński M, Jayaram B (2008) An introduction to fuzzy implications. In: Baczynski M, Jayaram B (eds) Fuzzy implications. Springer, Berlin, pp 1–35. https://doi.org/10.1007/978-3-540-69082-5_1
Chan CC (1998) A rough set approach to attribute generalization in data mining. Inf Sci 107(1–4):169–176. https://doi.org/10.1016/s0020-0255(97)10047-0
Chen HM, Li TR, Qiao SJ, Ruan D (2010) A rough set based dynamic maintenance approach for approximations in coarsening and refining attribute values. Int J Intell Syst 25(10):1005–1026. https://doi.org/10.1002/int.20436
Chen HM, Li TR, Ruan D, Lin JH, Hu CX (2013) A rough-set-based incremental approach for updating approximations under dynamic maintenance environments. IEEE Trans Knowl Data Eng 25(2):274–284. https://doi.org/10.1109/tkde.2011.220
Chen HM, Li TR, Luo C, Horng SJ, Wang GY (2014) A rough set-based method for updating decision rules on attribute values’ coarsening and refining. IEEE Trans Knowl Data Eng 26(12):2886–2899. https://doi.org/10.1109/tkde.2014.2320740
Chen HM, Li TR, Luo C, Horng SJ, Wang GY (2015) A decision-theoretic rough set approach for dynamic data mining. IEEE Trans Fuzzy Syst 23(6):1958–1970. https://doi.org/10.1109/tfuzz.2014.2387877
Chen YF, Yue XD, Fujita H, Fu SY (2017) Three-way decision support for diagnosis on focal liver lesions. Knowl Based Syst 127:85–99. https://doi.org/10.1016/j.knosys.2017.04.008
Cheng Y (2011) The incremental method for fast computing the rough fuzzy approximations. Data Knowl Eng 70(1):84–100. https://doi.org/10.1016/j.datak.2010.08.005
Grzymala-Busse JW (2004) Characteristic relations for incomplete data: a generalization of the indiscernibility relation. In: RSCTC 2004. LNCS, pp 244–253. https://doi.org/10.1007/978-3-540-25929-9_29
Grzymała-Busse JW (2005) Incomplete data and generalization of indiscernibility relation, definability, and approximations. In: International workshop on rough sets, fuzzy sets, data mining, and granular-soft computing, Springer, pp 244–253, https://doi.org/10.1007/11548669_26
Grzymała-Busse JW (2006) Rough set strategies to data with missing attribute values. In: Lin TY, Ohsuga S, Liau CJ, Hu X (eds) Foundations and novel approaches in data mining. Springer, Berlin, pp 197–212. https://doi.org/10.1007/11539827_11
Grzymała-Busse JW, Hu M (2000) A comparison of several approaches to missing attribute values in data mining. In: International conference on rough sets and current trends in computing, Springer, pp 378–385, https://doi.org/10.1007/3-540-45554-x_46
Guan LH, Wang GY (2012) Generalized approximations defined by non-equivalence relations. Inf Sci 193:163–179. https://doi.org/10.1016/j.ins.2012.01.009
Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH (2009) The weka data mining software: an update. J SIGKDD Explor Newsl 11(1):10–18. https://doi.org/10.1145/1656274.1656278
Hu J, Li TR, Luo C, Fujita H, Li SY (2017) Incremental fuzzy probabilistic rough sets over two universes. Int J Approx Reason 81:28–48. https://doi.org/10.1016/j.ijar.2016.11.002
Hu JH, Yang Y, Chen XH (2018) A novel todim method-based three-way decision model for medical treatment selection. Int J Fuzzy Syst 20(4):1240–1255. https://doi.org/10.1007/s40815-017-0320-3
Hu MJ, Yao YY (2019) Structured approximations as a basis for three-way decisions in rough set theory. Knowl Based Syst 165:92–109. https://doi.org/10.1016/j.knosys.2018.11.022
Huang JJ, Wang J, Yao YY, Zhong N (2017) Cost-sensitive three-way recommendations by learning pair-wise preferences. Int J Approx Reason 86:28–40. https://doi.org/10.1016/j.ijar.2017.03.005
Huang QQ, Li TR, Huang YY, Yang X, Fujita H (2019) Dynamic dominance rough set approach for processing composite ordered data. Knowl Based Syst. https://doi.org/10.1016/j.knosys.2019.06.037
Klement EP, Mesiar R, Pap E (2000) Triangular norms, trends in logic 8. Springer, Berlin
Kryszkiewicz M (1998) Rough set approach to incomplete information systems. Inf Sci 112(1–4):39–49. https://doi.org/10.1016/s0020-0255(98)10019-1
Lang GM, Miao DQ, Cai MJ (2017) Three-way decision approaches to conflict analysis using decision-theoretic rough set theory. Inf Sci 406–407:185–207. https://doi.org/10.1016/j.ins.2017.04.030
Lang GM, Miao DQ, Fujita H (2019) Three-way group conflict analysis based on pythagorean fuzzy set theory. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/tfuzz.2019.2908123
Leung Y, Ma JM, Zhang WX, Li TJ (2008) Dependence-space-based attribute reductions in inconsistent decision information systems. Int J Approx Reason 49(3):623–630. https://doi.org/10.1016/j.ijar.2008.06.004
Li SY, Li TR, Liu D (2013) Incremental updating approximations in dominance-based rough sets approach under the variation of the attribute set. Knowl Based Syst 40:17–26. https://doi.org/10.1016/j.knosys.2012.11.002
Li TR, Ruan D, Geert W, Song J, Xu Y (2007) A rough sets based characteristic relation approach for dynamic attribute generalization in data mining. Knowl Based Syst 20(5):485–494. https://doi.org/10.1016/j.knosys.2007.01.002
Lipski W (1981) On databases with incomplete information. J ACM 28(1):41–70. https://doi.org/10.1145/322234.322239
Liu D, Li TR, Ruan D, Zou WL (2009) An incremental approach for inducing knowledge from dynamic information systems. Fundam Inform 94(2):245–260. https://doi.org/10.3233/FI-2009-129
Liu D, Liang DC, Wang CC (2016) A novel three-way decision model based on incomplete information system. Knowl Based Syst 91:32–45. https://doi.org/10.1016/j.knosys.2015.07.036
Luo JF, Qin KY (2015) The rough set model based on grade indiscernibility relation. In: 2015 IEEE international conference on computer and information technology; Ubiquitous Computing and Communications; Dependable, Autonomic and Secure Computing; Pervasive Intelligence and Computing, pp 1366–1371. https://doi.org/10.1109/CIT/IUCC/DASC/PICOM.2015.203
Luo C, Li TR, Chen HM, Liu D (2013) Incremental approaches for updating approximations in set-valued ordered information systems. Knowl Based Syst 50:218–233. https://doi.org/10.1016/j.knosys.2013.06.013
Luo JF, Liu YY, Qin KY, Ding H (2017) Incremental update of rough set approximation under the grade indiscernibility relation. Int J Comput Intell Syst 10:212. https://doi.org/10.2991/ijcis.2017.10.1.15
Pawlak Z (1982) Rough sets. Int J Computer Inf Sci 11(5):341–356. https://doi.org/10.1007/BF01001956
Pawlak Z (1991) Rough sets: theoretical aspects of reasoning about data. Kluwer, Netherlands. https://doi.org/10.1007/978-94-011-3534-4
Pawlak Z (1998) Rough set theory and its applications to data analysis. Cybern Syst 29(7):661–688. https://doi.org/10.1080/019697298125470
Peters JF, Suraj Z, Shan S, Ramanna S, Pedrycz W, Pizzi N (2003) Classification of meteorological volumetric radar data using rough set methods. Pattern Recognit Lett 24(6):911–920. https://doi.org/10.1016/s0167-8655(02)00203-9
Qin KY, Luo JF, Pei Z (2015) Rough approximations based on valued tolerance relations. Fundam Inf 142(1–4):183–194. https://doi.org/10.3233/fi-2015-1290
Shan N, Ziarko W (1995) Data-based acquisition and incremental modification of classification rules. Comput Intell 11(2):357–370. https://doi.org/10.1111/j.1467-8640.1995.tb00038.x
Stefanowski J, Tsoukias A (2001) Incomplete information tables and rough classification. Comput Intell 17(3):545–566. https://doi.org/10.1111/0824-7935.00162
Sun L, Wang W, Xu JC, Zhang SG (2019a) Improved LLE and neighborhood rough sets-based gene selection using lebesgue measure for cancer classification on gene expression data. J Intell Fuzzy Syst 37:1–12. https://doi.org/10.3233/jifs-181904 (Preprint)
Sun L, Zhang XY, Qian YH, Xu JC, Zhang SG (2019b) Feature selection using neighborhood entropy-based uncertainty measures for gene expression data classification. Inf Sci. https://doi.org/10.1016/j.ins.2019.05.072
Wang GY (2002) Extension of rough set under incomplete information systems. J Comput Res Dev 10(4):1–9. https://doi.org/10.1109/fuzz.2002.1006657
Wang P, Zhang PF, Li ZW (2019) A three-way decision method based on gaussian kernel in a hybrid information system with images: an application in medical diagnosis. Appl Soft Comput 77:734–749. https://doi.org/10.1016/j.asoc.2019.01.031
Yao YY, Greco S, Słowiński R (2015) Probabilistic rough sets. In: Kacprzyk J, Pedrycz W (eds) Springer handbook of computational intelligence. Springer, Berlin, pp 387–411. https://doi.org/10.1007/978-3-662-43505-2_24
Yao YY (2010) Three-way decisions with probabilistic rough sets. Inf Sci 180(3):341–353. https://doi.org/10.1016/j.ins.2009.09.021
Yao YY (2015) The two sides of the theory of rough sets. Knowl Based Syst 80:67–77. https://doi.org/10.1016/j.knosys.2015.01.004
Yao YY (2018) Three-way decision and granular computing. Int J Approx Reason 103:107–123. https://doi.org/10.1016/j.ijar.2018.09.005
Yao YY (2019) Three-way conflict analysis: reformulations and extensions of the pawlak model. Knowl Based Syst 180:26–37. https://doi.org/10.1016/j.knosys.2019.05.016
Yin XR, Jia XY, Shang L (2006) A new extension model of rough sets under incomplete information. In: International conference on rough sets and knowledge technology, Springer, pp 141–146. https://doi.org/10.1007/11795131_21
Zhang HR, Min F, Shi B (2017) Regression-based three-way recommendation. Inf Sci 378:444–461. https://doi.org/10.1016/j.ins.2016.03.019
Zhang JB, Li TR, Ruan D, Liu D (2012a) Rough sets based matrix approaches with dynamic attribute variation in set-valued information systems. Int J Approx Reason 53(4):620–635. https://doi.org/10.1016/j.ijar.2012.01.001
Zhang XH, Zhou B, Li P (2012b) A general frame for intuitionistic fuzzy rough sets. Inf Sci 216:34–49. https://doi.org/10.1016/j.ins.2012.04.018
Acknowledgements
This study was funded by National Natural Science Foundation of China (Grant Nos. 61473239, 11501470, 61673285) and the China Scholarship Council (Grant No. 201707000052).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Junfang Luo, Keyun Qin, Yimeng Zhang, and Xue Rong Zhao declare that they have no conflict of interest.
Human and animal rights
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by A. Di Nola.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Luo, J., Qin, K., Zhang, Y. et al. Incrementally updating approximations based on the graded tolerance relation in incomplete information tables. Soft Comput 24, 8655–8671 (2020). https://doi.org/10.1007/s00500-020-04838-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-020-04838-3