Skip to main content
Springer Nature Link
Log in

Solving variable-order fractional differential algebraic equations via generalized fuzzy hyperbolic model with application in electric circuit modeling

  • Methodologies and Application
  • Published:
Soft Computing Aims and scope Submit manuscript

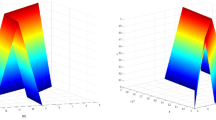
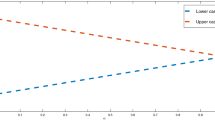
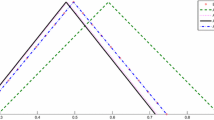
Abstract

In this paper, a new approach based on a generalized fuzzy hyperbolic model is used for the numerical solution of variable-order fractional differential algebraic equations. The fractional derivative is described in the Atangana–Baleanu sense that is a new derivative with fractional order based on the generalized Mittag–Leffler function. First, by using fuzzy solutions with adjustable parameters, the variable-order fractional differential algebraic equations are reduced to a problem consisting of solving a system of algebraic equations. For adjusting the parameters of fuzzy solutions, an unconstrained optimization problem is then considered. A learning algorithm is also presented for solving the unconstrained optimization problem. Finally, some numerical examples are given to verify the efficiency and accuracy of the proposed approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Atangana A, Alqahtani RT (2016) Stability analysis of nonlinear thin viscous fluid sheet flow equation with local fractional variable-order derivative. J Comput Theor Nanosci 13:2710–17

    Google Scholar 

  • Bazaraa MS, Sherali HD, Shetty CM (2006) Nonlinear programming: theory and algorithms, 3rd edn. Wiley, Hoboken

    MATH  Google Scholar 

  • Bendtsen C, Thomsen PG (1999) Numerical solution of differential algebraic equations, technical report, Department of Mathematical Modelling, Technical University of Denmark, Lyngby, Denmark

  • Boulkaibet I, Belarbi K, Bououden S, Marwala T, Chadli M (2017) A new T–S fuzzy model predictive control for nonlinear processes. Expert Syst Appl 88:132–151

    Google Scholar 

  • Buckley JJ (1992) Universal fuzzy controllers. Automatica 28:1245–1248

    MathSciNet  MATH  Google Scholar 

  • Cao J, Qiu Y, Song G (2017) A compact finite difference scheme for variable order subdiffusion equation. Commun Nonlinear Sci Numer Simul 48:140–149

    MathSciNet  MATH  Google Scholar 

  • Chen YY, Chang YT, Chen BS (2009) Fuzzy solutions to partial differential equations: adaptive approach. IEEE Trans Fuzzy Syst 17(1):116–127

    Google Scholar 

  • Chen Y-M, Wei Y-Q, Liu D-Y, Yu H (2015) Numerical solution for a class of nonlinear variable order fractional differential equations with Legendre wavelets. Appl Math Lett 46:83–88

    MathSciNet  MATH  Google Scholar 

  • Coronel-Escamilla A, Gómez-Aguilar JF, Torres L, Escobar-Jiménez RF (2018) A numerical solution for a variable-order reaction–diffusion model by using fractional derivatives with non-local and non-singular kernel. Phys A 491:406–24

    MathSciNet  Google Scholar 

  • Cui Y, Zhang HG, Wang Y, Gao W (2016) Adaptive control for a class of uncertain strict-feedback nonlinear systems based on a generalized fuzzy hyperbolic model. Fuzzy Sets Syst 302:52–64

    MathSciNet  MATH  Google Scholar 

  • Dang QV et al (2017) Robust stabilizing controller design for Takagi–Sugeno fuzzy descriptor systems under state constraints and actuator satu-ration. Fuzzy Sets Syst 329:77–90

    MATH  Google Scholar 

  • Deng W, Zhao H, Zou L, Li G, Yang X, Wu D (2017a) A novel collaborative optimization algorithm in solving complex optimization problems. Soft Comput 21:4387–4398

    Google Scholar 

  • Deng W, Zhao H, Yang X, Xiong J, Sun M, Li B (2017b) Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment. Appl Soft Comput 59:288–302

    Google Scholar 

  • Deng W, Xu J, Zhao H (2019) An improved ant colony optimization algorithm based on hybrid strategies for scheduling problem. IEEE Access 7:20281–20292

    Google Scholar 

  • Dong J, Fu Y (2017) A design method for T–S fuzzy systems with partly immeasurable premise variables subject to actuator saturation. Neurocomputing 225:164–173

    Google Scholar 

  • Fu Z, Chen W, Ling L (2015) Method of approximate particular solutions for constant- and variable-order fractional diffusion models. Eng Anal Bound Elem 57:37–46

    MathSciNet  MATH  Google Scholar 

  • Ghanbari B, Gómez-Aguilar JF (2018) Modeling the dynamics of nutrient–phytoplankton–zooplankton system with variable-order fractional derivatives. Chaos, Solitons Fractals 116:114–120

    MathSciNet  MATH  Google Scholar 

  • Ghanbari F, Ghanbari K, Mokhtary P (2018) Generalized Jacobi–Galerkin method for nonlinear fractional differential algebraic equations. Comput Appl Math 37(4):5456–5475

    MathSciNet  MATH  Google Scholar 

  • Ghomanjani F (2017) A new approach for solving fractional differential–algebraic equations. J Taibah Univ Sci 11:1158–1164

    Google Scholar 

  • Gómez-Aguilar JF (2018) Analytical and numerical solutions of a nonlinear alcoholism model via variable-order fractional differential equations. Phys A 494:52–75

    MathSciNet  Google Scholar 

  • Jia Y, Xu M, Lin Y (2017) A numerical solution for variable order fractional functional differential equation. Appl Math Lett 64:125–130

    MathSciNet  MATH  Google Scholar 

  • Karabacak M, Celik E (2013) The numerical solution of fractional differential-algebraic equations (FDAEs). New Trends Math Sci 1(2):1–6

    Google Scholar 

  • Kosko B (1994) Fuzzy systems as universal approximators. IEEE Trans Comput 43(11):1329–1333

    MATH  Google Scholar 

  • Lee KY, El-Sharkawi MA (2008) Modern heuristic optimization techniques: theory and applications to power systems. Wiley, Hoboken

    Google Scholar 

  • Li X, Wu B (2017) A new reproducing kernel method for variable order fractional boundary value problems for functional differential equations. J Comput Appl Math 311:387–393

    MathSciNet  MATH  Google Scholar 

  • Li X, Li H, Wu B (2017) A new numerical method for variable order fractional functional differential equations. Appl Math Lett 68:80–86

    MathSciNet  MATH  Google Scholar 

  • Liu H, Fu Y, Li B (2017) Discrete waveform relaxation method for linear fractional delay differential-algebraic equations. Discrete Dyn Nat Soc 6306570:9 pages

  • Liu S, Guo Z, Zhang HG (2008) Fuzzy hyperbolic neural network model and its application in H1 filter design, In: Sun F et al (eds) Proceedings of the 5th international symposium on neural networks: advances in neural networks, part I, LNCS 5263, Springer, Berlin, 2008, pp 222–230

  • Mei W, Bullo F (2017) Lasalle invariance principle for discrete-time dynamical systems: a concise and self-contained tutorial. arXiv preprint arXiv:1710.03710

  • Miller KS, Ross B (1993) An introduction to the fractional calculus and fractional differential equations. Wiley, New York

    MATH  Google Scholar 

  • Mirzajani S, PourmahmoodAghababa M, Heydari A (2019) Adaptive T–S fuzzy control design for fractional-order systems withparametric uncertainty and input constraint. Fuzzy Sets Syst 365(15):22–39

    MATH  Google Scholar 

  • Muthukumar P, Balasubramaniam P, Ratnavelu K (2016) T–S fuzzy predictive control for fractional order dynamical systems and its applications. Nonlinear Dyn 86(2):751–763

    MATH  Google Scholar 

  • Nocedal J, Wright S (2006) Numerical Optimization, second edn. Springer- Verlag, Berlin, NewYork

    MATH  Google Scholar 

  • Pakdaman M, Effati S (2016) Approximating the solution of optimal control problems by fuzzy systems. Neural Process Lett 43(3):667–686

    Google Scholar 

  • Pham VT, Vaidyanathan S, Volos C, Kapitaniak T (2018) Nonlinear dynamical systems with self-excited and hidden attractors. Springer, Berlin

    MATH  Google Scholar 

  • Sh DM, Hassani H (2017) An optimization method based on the generalized polynomials for nonlinear variable-order time fractional diffusion-wave equation. Nonlinear Dyn 88:1587–1598

    MathSciNet  MATH  Google Scholar 

  • Shen S, Liu F, Anh V, Turner I, Chen J (2013) A characteristic difference method for the variable-order fractional advection–diffusion equation. J Appl Math Comput 42:371–386

    MathSciNet  MATH  Google Scholar 

  • Shen H, Su L, Park JH (2017) Reliable mixed/passive control for T–S fuzzy delayed systems based on a semi-Markov jump model approach. Fuzzy Sets Syst 314:79–98

    MathSciNet  MATH  Google Scholar 

  • Shiri B, Baleanu D (2019) System of fractional differential algebraic equations with applications. Chaos Solitons Fractals 120:203–212

    MathSciNet  Google Scholar 

  • Solís-Pérez JE, Gómez-Aguilar JF, Atangana A (2018) Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag–Leffler laws. Chaos Solitons Fractals 114:175–185

    MathSciNet  MATH  Google Scholar 

  • Sun H, Chen W, Li CH, Chen Y (2012) Finite difference schemes for variable-order time fractional diffusion equation. Int J Bifurc Chaos 22:1250085

    MathSciNet  MATH  Google Scholar 

  • Sun Q, Wang Y, Yang J, Qiu Y, Zhang H (2014) Chaotic dynamics in smart grid and suppression scheme via generalized fuzzy hyperbolic model. Math Probl Eng 2014, Article ID 761271, 7 pages

  • Sun H, Zhang Y, Baleanu D, Chen W, Chen Y (2018) A new collection of real world applications of fractional calculus in science and engineering. Commun Nonlinear Sci Numer Simul 64:213–231

    Google Scholar 

  • Takagi T, Sugeno M (1985) Fuzzy identification of systems and its applications to modeling and control. IEEE Trans Syst Man Cybern 15(1):116–132

    MATH  Google Scholar 

  • Wang LX (1992) Fuzzy systems are universal approximators. In: Proceedings 1EEE international conference on fuzzy systems (San Diego), pp 1163–1170

  • Wang L, Chen N (2014) The predictor-corrector solution for fractional order differential algebraic equation. In: CFDA’14 international conference on fractional differentiation and its applications

  • Wang SH, Jhu WL, Yung CF, Wang PF (2011) Numerical solutions of differential algebraic equations and its applications in solving TPPC problems. J Mar Sci Technol 19:76–88

    Google Scholar 

  • Wu ZG, Dong SH, Shi P, Su H, Huang T, Lu R (2017) Fuzzy-model-based nonfragile guaranteed cost control of nonlinear markov jump systems. IEEE Trans Syst Man Cybern Syst 47(8):1–10

    Google Scholar 

  • Xu T, Lu S, Chen W, Chen H (2018) Finite difference scheme for multi-term variable-order fractional diffusion equation. Adv Differ Equ 103:1–13

    MathSciNet  MATH  Google Scholar 

  • Yaghoobi S, Moghaddam BP, Ivaz K (2017) An efficient cubic spline approximation for variable-order fractional differential equations with time delay. Nonlinear Dyn 87:815–826

    MathSciNet  MATH  Google Scholar 

  • Yang XJ (2017) Fractional derivatives of constant and variable orders applied to anomalous relaxation models in heat-transfer problems. Therm Sci 21:1161–1171

    Google Scholar 

  • Ying H (1994) Sufficient conditions on general fuzzy systems as function approximators. Automatica 30:521–525

    MATH  Google Scholar 

  • Zak SH (2003) Systems and control. Oxford University Press, Oxford

    Google Scholar 

  • Zeng XJ, Singh MG (1995) Approximation theory of fuzzy systems-MIMO case. IEEE Trans Fuzzy Syst 3(2):219–235

    Google Scholar 

  • Zhang X-S (2000) Neural networks in optimization. Kluwer Academic Publishers, Dordrecht

    MATH  Google Scholar 

  • Zhang HG, Yongbing Q (2001) Modeling, identification, and control of a class of nonlinear systems. IEEE Trans Fuzzy Syst 9(2):349–354

    MATH  Google Scholar 

  • Zhang M, Zhang H (2005) Modeling and control based on generalized fuzzy hyperbolic model. In: American control conference

  • Zhang M, Zhang H (2006) Robust adaptive fuzzy control scheme for nonlinear system with uncertainty. J Control Theory Appl 4(2):209–216

    MathSciNet  MATH  Google Scholar 

  • Zhang HG, Wang Z, Liu D (2003) Chaotifying fuzzy hyperbolic model using adaptive inverse optimal control approach. Int J Bifurc Chaos 12:32–43

    Google Scholar 

  • Zhang HG, Wang ZL, Li M, Quan B, Zhang MG (2004a) Generalized fuzzy hyperbolic model: a universal approximator. Acta Autom Sin 30(3):416–422

    MathSciNet  Google Scholar 

  • Zhang HG, Wang ZL, Li M, Quan B, Zhang MJ (2004b) Generalized fuzzy hyperbolic model: a universal approximator. Acta Autom Sin 30(3):416–422

    MathSciNet  Google Scholar 

  • Zhang M, Zhang H, Liu D (2004c) A generalized fuzzy hyperbolic modeling and control scheme. In: IEEE international conference on fuzzy systems

  • Zhang HG, Wang Z, Liu D (2005) Chaotifying fuzzy hyperbolic model using impulsive and nonlinear feedback control approaches. Int J Bifurc Chaos 15(8):2603–2610

    MathSciNet  MATH  Google Scholar 

  • Zhang JL, Zhang HG, Luo YH, Liang HJ (2013) Nearly optimal control scheme using adaptive dynamic programming based on generalized fuzzy hyperbolic model. Acta Autom Sin 39(2):142–148

    MathSciNet  MATH  Google Scholar 

  • Zhao H, Liu H, Xu J, Deng W (2019a) Performance prediction using high-order differential mathematical morphology gradient spectrum entropy and extreme learning machine. IEEE Trans Instrum Meas. https://doi.org/10.1109/TIM.2019.2948414

    Article  Google Scholar 

  • Zhao H, Zheng J, Xu J, Deng W (2019b) Fault diagnosis method based on principal component analysis and broad learning system. IEEE Access 7:99263–99272

    Google Scholar 

  • Zhao H, Zheng J, Deng W, Song Y (2020) Semi-supervised broad learning system based on manifold regularization and broad network. IEEE Trans Circuits Syst I Regul Pap 67(3):983–994

    MathSciNet  Google Scholar 

  • Zhu Q, Azar AT (2015) Complex system modelling and control through intelligent soft computations. Springer, Berlin

    MATH  Google Scholar 

  • Zurigat M, Momani SH, Alawneh A (2010) Analytical approximate solutions of systems of fractional algebraic differential equations by homotopy analysis method. Comput Math Appl 59:1227–1235

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This study was not funded by any grant.

Author information

Authors and Affiliations

  1. Faculty of Mathematical Sciences, Shahrood University of Technology, Shahrood, Iran

    Marzieh Mortezaee, Mehdi Ghovatmand & Alireza Nazemi

Authors
  1. Marzieh Mortezaee
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mehdi Ghovatmand
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Alireza Nazemi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mehdi Ghovatmand.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Communicated by V. Loia.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mortezaee, M., Ghovatmand, M. & Nazemi, A. Solving variable-order fractional differential algebraic equations via generalized fuzzy hyperbolic model with application in electric circuit modeling. Soft Comput 24, 16745–16758 (2020). https://doi.org/10.1007/s00500-020-04969-7

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-020-04969-7

Keywords