Abstract
In this paper, we investigate some aspects of Spencer–Brown’s Calculus of Indications. Drawing from earlier work by Kauffman and Varela, we present a new categorical framework that allows to characterize the construction of infinite arithmetic expressions as sequences taking values in grossone.














Similar content being viewed by others
Notes
The introduction of the numeral ① may require, in some contexts, the augmentation of the set of natural \({\mathbb {N}}\) to a larger set \(\hat{{\mathbb {N}}}\), where
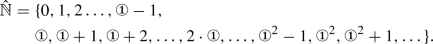
For the purpose of this paper we will not need to make use of \(\hat{{\mathbb {N}}}\).
Evidence of the efficacy of the grossone approach is highlighted by its successful application to many fields of applied mathematics, including optimization (see Cococcioni et al. 2018, 2020; De Cosmis and De Leone 2012; Sergeyev et al. 2018; Iavernaro et al. 2020; Iudin et al. 2012; Sergeyev 2007, 2013b; Zhigljavsky 2012), fractals and cellular automata (see Caldarola 2018; D’Alotto 2012, 2015, 2013) as well as infinite decision-making processes, game theory, and probability (see Fiaschi and Cococcioni 2018; Rizza 2018, 2019), whereas the formal logical foundation of grossone has been investigated in Lolli (2012); Margenstern (2011); Montagna et al. (2015). The approach presented in this paper bears similarities to the application of grossone to Turing machines as described in Sergeyev and Garro (2010). Further investigation of these analogies remains open.
The two systems are slightly different in terms of their rules of deduction (or rewriting). We do not examine this point any further in this paper.
The relevance of grossone to this construction will appear in the subsequent sections.
Here the objects are the natural numbers, and there is a morphism between two natural numbers \(m\rightarrow n\) if and only if \(m\ge n\). The choice of reversing the natural order is made in order for the functor F to be contravariant.
The condition given here guarantees that all nested cuts are of at most depth \(n-1\).
A monic arrow in any category is defined as follows. Given any morphism \(f: A\longrightarrow B\), f is said to be monic if, for any two morphisms \(g,h: Z\longrightarrow A\) such that \(f\circ g=f\circ h\), it is the case that \(g=h\).
\(\coprod \) is well defined in \({\mathcal {CI}}\) since it is a topos.
A formal categorical characterization of a variant of this procedure, applied to cuts-only \(\alpha \) graphs can found in Gangle et al. (2020).
Note that it is important to distinguish this operator
 (as an operation on \(\alpha \)) from the circle drawn around 1 in the grossone numeral ① .
(as an operation on \(\alpha \)) from the circle drawn around 1 in the grossone numeral ① .
References
Barwise J, Etchemendy J (1989) The liar: an essay on truth and circularity. Oxford University Press, New York
Caldarola F (2018) The Sierpinski curve viewed by numerical computations with infinities and infinitesimals. Appl Math Comput 318:321–328
Caterina G, Gangle R (2013) Iconicity and abduction: a categorical approach to creative hypothesis-formation in Peirce’s existential graphs. Logic J IGPL 21(6):1028–1043
Caterina G, Gangle R (2016) Iconicity and abduction. Springer, New York
Cococcioni M, Pappalardo M, Sergeyev YD (2018) Lexicographic multi-objective linear programming using grossone methodology: theory and algorithm. Appl Math Comput 318:298–311
Cococcioni M, Cudazzo A, Pappalardo M, Sergeyev YD (2020) Solving the lexicographic multi-objective mixed-integer linear programming problem using branch-and-bound and grossone methodology. Commun Nonlinear Sci Numer Simul 84:1–20
D’Alotto L (2012) Cellular automata using infinite computations. Appl Math Comput 218(16):8077–8082
D’Alotto L (2013) A classification of two-dimensional cellular automata using infinite computations. Indian J Math 55:143–158
D’Alotto L (2015) A Classification of One-Dimensional Cellular Automata using Infinite Computations. Applied Mathematics and Computation 255:15–24
De Cosmis S, De Leone R (2012) The use of grossone in mathematical programming and operations research. Appl Math Comput 218(16):8029–8038
Fiaschi L, Cococcioni M (2018) Numerical asymptotic results in game theory using Sergeyev’s infinity computing. Int J Unconvent Comput 14(1):1–25
Gangle R, Caterina G, Tohme F (2020) A generic figures reconstruction of Peirce’s Existential Graphs (Alpha). Erkenntnis. https://doi.org/10.1007/s10670-019-00211-5
Iavernaro F, Mazzia F, Mukhametzhanov MS, Sergeyev YD (2020) Conjugate-symplecticity properties of Euler–Maclaurin methods and their implementation on the infinity computer. Appl Numer Math 155:58–72
Iudin D, Sergeyev YD, Hayakawa M (2012) Interpretation of percolation in terms of infinity computations. Appl Math Comput 218(16):8099–8111
Kauffman LH (2012) Laws of Form: an Exploration in Mathematics and Foundations. http://homepages.math.uic.edu/~kauffman/Laws.pdf
Kauffman LH, Varela FJ (1980) Form dynamics. J Soc Biol Struct 3:171–206
Lolli G (2012) Infinitesimals and infinites in the history of mathematics: a brief survey. Appl Math Comput 218(16):7979–7988
Luhmann N (1995) Social systems. Stanford University Press, Stanford
Mac Lane S (1998) Categories for the working mathematician. Springer, Berlin
Margenstern M (2011) Using Grossone to count the number of elements of infinite sets and the connection with bijections. p-Adic Numbers. Ultrametric Anal Appl 3(3):196–204
Montagna F, Simi G, Sorbi A (2015) Taking the Pirahã seriously. Commun Nonlinear Sci Numer Simul 21(1–3):52–69
Reyes M, Reyes G, Zolfaghari H (2004) Generic figures and their glueings. Polimetrica, Milan
Rizza D (2018) A study of mathematical determination through Bertrand’s Paradox. Philosophia Mathematica 26(3):375–395
Rizza D (2019) Numerical methods for infinite decision-making processes. Int J Unconvent Comput 14(2):139–158
Sergeyev YD (2013a). Arithmetic of infinity. Edizioni Orizzonti Meridionali, 2nd edition
Sergeyev YD (2007) Blinking fractals and their quantitative analysis using infinite and infinitesimal numbers. Chaos, Solitons Fract 33:50–75
Sergeyev YD (2010) Computer system for storing infinite, infinitesimal, and finite quantities and executing arithmetical operations with them. USA Patent 7(860):914
Sergeyev YD (2013b) Solving ordinary differential equations by working with infinitesimals numerically on the Infinity Computer. Appl Math Comput 219(22):10668–10681
Sergeyev YD (2017) Numerical infinities and infinitesimals: methodology, applications, and repercussions on two Hilbert problems. EMS Surv Math Sci 4(2):219–320
Sergeyev YD, Garro A (2010) Observability of turing machines: a refinement of the theory of computation. Informatica 21(3):425–454
Sergeyev YD, Kvasov DE, Mukhametzhanov MS (2018) On strong homogeneity of a class of global optimization algorithms working with infinite and infinitesimal scales. Commun Nonlinear Sci Numer Simul 59:319–330
Spencer-Brown G (1969) Laws of form. Allen & Unwin, London
Tohmé F, Caterina G, Gangle Rocco (2020) Computing Truth Values in the Topos of \(\alpha \)-Infinite Peirce’s Existential Graphs. In press, Applied Mathematics and Computation
Varela F, Goguen JA (1978) The arithmetic of closure. J Cybern 8:291–324
Zalamea F (2010) Towards a complex variable interpretation of Peirce’s existential graphs. In: Bergman M et al (eds) Ideas in action. Proceedings of the applying peirce conference, Nordic Pragmatism Network, Helsinki, pp 254–264
Zeman J (1974) Peirce’s logical graphs. Semiotica 12:239–256
Zhigljavsky A (2012) Computing sums of conditionally convergent and divergent series using the concept of Grossone. Appl Math Comput 218:8064–8076
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that they have no conflict of interest.
Human and animal rights
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by Yaroslav D. Sergeyev.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Gangle, R., Caterina, G. & Tohmé, F. A constructive sequence algebra for the calculus of indications. Soft Comput 24, 17621–17629 (2020). https://doi.org/10.1007/s00500-020-05121-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-020-05121-1





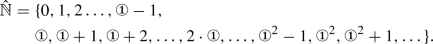
 (as an operation on
(as an operation on