Skip to main content
SpringerLink
Log in

A novel fuzzy approach for segmenting medical images

  • Methodologies and Application
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

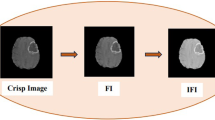
In various medical imaging studies, the segmentation of the medical image is a crucial step. Due to the inherent behavior of the images, the computerized tomography (CT) scan/magnetic resonance imaging (MRI) images are not clear. As the medical images are captured using electronic devices, these images are ambiguous and unclear. This ambiguity in the images is due to factors related to noise and the environment while capturing images. A fuzzy set is a valuable method to deal with data uncertainty. In this paper, a novel clustering approach based upon a fuzzy concept is proposed, which enhances the vague MRI/CT scan image before segmentation. Initially, the image noise is minimized by processing eight immediate neighborhood pixels around each pixel in an image. After noise processing, upper and lower membership levels of the image are computed. Hamacher T-conorm is used as an aggregation operator to construct a new membership function using upper and lower membership levels. The enhanced image, created using the new membership function, is then segmented using Gaussian kernel-based fuzzy c means clustering. The experiment is performed on MRI/CT scan brain tumor images. Real data experiments demonstrate that the proposed algorithm has better performance when compared with existing methods both quantitatively and qualitatively. It is observed that even in the presence of noise, the proposed method exhibits better efficiency.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Abualigah L (2020a) Group search optimizer: a nature-inspired meta-heuristic optimization algorithm with its results, variants, and applications. Neural Comput Appl:1–24

  • Abualigah L (2020b) Multi-verse optimizer algorithm: a comprehensive survey of its results, variants, and applications. Neural Comput Appl:1–21

  • Abualigah L, Diabat A (2020a) A comprehensive survey of the grasshopper optimization algorithm: results, variants, and applications. Neural Comput Appl:1–24

  • Abualigah L, Diabat A (2020b) A novel hybrid antlion optimization algorithm for multi-objective task scheduling problems in cloud computing environments. Cluster Comput:1–19

  • Abualigah LM, Khader AT (2017) Unsupervised text feature selection technique based on hybrid particle swarm optimization algorithm with genetic operators for the text clustering. J Supercomput 73(11):4773–4795

    Article  Google Scholar 

  • Abualigah LM, Khader AT, Hanandeh ES, Gandomi AH (2017) A novel hybridization strategy for krill herd algorithm applied to clustering techniques. Appl Soft Comput 60:423–435

    Article  Google Scholar 

  • Abualigah LM, Khader AT, Hanandeh ES (2018a) A combination of objective functions and hybrid krill herd algorithm for text document clustering analysis. Eng Appl Artif Intell 73:111–125

    Article  Google Scholar 

  • Abualigah LM, Khader AT, Hanandeh ES (2018b) Hybrid clustering analysis using improved krill herd algorithm. Appl Intell 48(11):4047–4071

    Article  Google Scholar 

  • Abualigah LM, Khader AT, Hanandeh ES (2018c) A new feature selection method to improve the document clustering using particle swarm optimization algorithm. J Comput Sci 25:456–466

    Article  Google Scholar 

  • Abualigah LMQ (2019) Feature selection and enhanced krill herd algorithm for text document clustering. Springer, Berlin

    Book  Google Scholar 

  • Abualigah LMQ, Hanandeh ES (2015) Applying genetic algorithms to information retrieval using vector space model. Int J Comput Sci Eng Appl 5(1):19

    Google Scholar 

  • Atanassov KT (1999) Intuitionistic fuzzy sets. In: Intuitionistic fuzzy sets. Springer, pp 1–137

  • Bezdek JC (1981) Objective function clustering. In: Pattern recognition with fuzzy objective function algorithms. Springer, pp 43–93

  • Chaira T (2011) A novel intuitionistic fuzzy C means clustering algorithm and its application to medical images. Appl Soft Comput 11(2):1711–1717

    Article  Google Scholar 

  • Chaira T (2013) Contrast enhancement of medical images using type II fuzzy set. In: 2013 national conference on communications (NCC). IEEE, pp 1–5

  • Chaira T (2014) An improved medical image enhancement scheme using type II fuzzy set. Appl Soft Comput 25:293–308

    Article  Google Scholar 

  • Chaira T (2019) Fuzzy set and its extension. Wiley Online Library, Hoboken

    Book  Google Scholar 

  • Chintalapudi KK, Kam M (1998) A noise-resistant fuzzy C means algorithm for clustering. In: 1998 IEEE international conference on fuzzy systems proceedings. IEEE World Congress on Computational Intelligence (Cat. No. 98CH36228), vol 2. IEEE, pp 1458–1463

  • Dombi J (1982) A general class of fuzzy operators, the demorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst 8(2):149–163

    Article  MathSciNet  Google Scholar 

  • Ensafi P, Tizhoosh HR (2005) Type-2 fuzzy image enhancement. In: International conference image analysis and recognition. Springer, pp 159–166

  • Kaur P (2016) Improved version of kernelized fuzzy C means using credibility. Int J Comput Sci Netw 5(1):50–54

    Google Scholar 

  • Kaur P, Lamba I, Gosain A (2011a) Kernelized type-2 fuzzy C-means clustering algorithm in segmentation of noisy medical images. In: 2011 IEEE recent advances in intelligent computational systems. IEEE, pp 493–498

  • Kaur P, Lamba I, Gosain A (2011b) A robust method for image segmentation of noisy digital images. In: 2011 IEEE international conference on fuzzy systems (FUZZ-IEEE 2011). IEEE, pp 1656–1663

  • Kaur P, Soni A, Gosain A, India II (2012) Novel intuitionistic fuzzy C-means clustering for linearly and nonlinearly separable data. WSEAS Trans Comput 11(3):65–76

    Google Scholar 

  • Kaur P, Soni A, Gosain A (2013a) Image segmentation of noisy digital images using extended fuzzy C-means clustering algorithm. Int J Comput Appl Technol 47(2–3):198–205

    Article  Google Scholar 

  • Kaur P, Soni A, Gosain A (2013b) Robust kernelized approach to clustering by incorporating new distance measure. Eng Appl Artif Intell 26(2):833–847

    Article  Google Scholar 

  • Masulli F, Schenone A (1999) A fuzzy clustering based segmentation system as support to diagnosis in medical imaging. Artif Intell Med 16(2):129–147

    Article  Google Scholar 

  • Matlab V (2018) 9.4.0.813654 (r2018a). The MathWorks Inc., Natick, MA

    Google Scholar 

  • Mendel JM (2007) Type-2 fuzzy sets and systems: an overview. IEEE Comput Intell Mag 2(1):20–29

    Article  Google Scholar 

  • Mendel JM, John RB (2002) Type-2 fuzzy sets made simple. IEEE Trans Fuzzy Syst 10(2):117–127

    Article  Google Scholar 

  • Rhee FCH, Hwang C (2001) A type-2 fuzzy c-means clustering algorithm. In: Proceedings joint 9th IFSA world congress and 20th NAFIPS international conference (Cat. No. 01TH8569), vol 4. IEEE, pp 1926–1929

  • Tsai DM, Lin CC (2011) Fuzzy c-means based clustering for linearly and nonlinearly separable data. Pattern Recogn 44(8):1750–1760

    Article  Google Scholar 

  • Weber S (1983) A general concept of fuzzy connectives, negations and implications based on t-norms and t-conorms. Fuzzy Sets Syst 11(1–3):115–134

    Article  MathSciNet  Google Scholar 

  • Yager RR, RR Y (1980) On a general class of fuzzy connectives

  • Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353

    Article  Google Scholar 

  • Zhang DQ, Chen SC (2003) Clustering incomplete data using kernel-based fuzzy C-means algorithm. Neural Process Lett 18(3):155–162

    Article  Google Scholar 

  • Zhang DQ, Chen SC (2004) A novel kernelized fuzzy C-means algorithm with application in medical image segmentation. Artif Intell Med 32(1):37–50

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Maharaja Surajmal Institute of Technology, GGSIP University, New Delhi, India

    Prabhjot Kaur

  2. Aravali Pharma and Lifesciences, Dwarka, New Delhi, India

    Tamalika Chaira

Authors
  1. Prabhjot Kaur
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tamalika Chaira
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Prabhjot Kaur.

Ethics declarations

Conflict of interest

All the authors declare that there is no conflict of interest in publishing this paper.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Communicated by V. Loia.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kaur, P., Chaira, T. A novel fuzzy approach for segmenting medical images. Soft Comput 25, 3565–3575 (2021). https://doi.org/10.1007/s00500-020-05386-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-020-05386-6

Keywords

Search

Navigation