Inventory policies for seasonal items with logistic-growth demand rate under fully permissible delay in payment: a neutrosophic optimization approach

Abstract

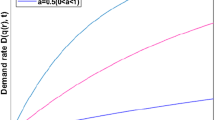
The present study investigates an inventory system for seasonal products under variable demand rate and partial backordering in a competitive market. Among various demand rate functions used in the existing literature of economic order quantity (EOQ) models, the logistic-growth function is best known to estimate market already captured and fraction of market remaining to be captured by new seasonal and technology driven items. Weibull distribution well represents the seasonality and versatility of these products. Due to retailers’ reluctance to purchase and store these perishable products, supplier offers the delay in payment. In view of the above, the proposed EOQ model suitable for those items considers the logistic-growth demand rate, Weibull distribution deterioration rate and partial backordering along with fully permissible delay in payment. Since the neutrosophic set quantifies the imprecise information in real-life scenarios, the proposed EOQ model is optimized in neutrosophic environment. A general unconstrained nonlinear mathematical model with neutrosophic coefficients is optimized using the weighted arithmetic mean function, subject to specified neutrosophic norm. A special case with the neutrosophic conjunction norm along with four lemmata is considered to minimize the cost functions with neutrosophic coefficients to proposed EOQ model across various trade-credit intervals. Here, the managerial insights identified through sensitivity analysis advocate to reduce the expenses on early promotions for foreshortening the demand at the beginning of cycle. Also, the present study demonstrates the optimal inventory depletion time to depend on the demand during the shortages in neutrosophic environment.

Appendices

Appendix A

Let X be the space of objects, in which a generic element is denoted by x.

Definition 3

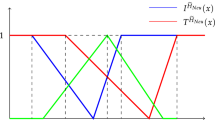
(Wang et al. 2010) A NS set A in X is characterized by truth-membership function $\mu _{A}{(x)}$, indeterminacy-membership function $\sigma _{A}{(x)}$ and falsity-membership function $\nu _{A}{(x)}$. Here, $\mu _{A}{(x)}: X \xrightarrow {}$ $]0^-,1^+[$, $\sigma _{A}{(x)}: X \xrightarrow {}$ $]0^-,1^+[$ and $\nu _{A}{(x)}: X \xrightarrow {}$ $]0^-,1^+[$ are real standard or non-standard subsets of $]0^-,1^+[$ and satisfy the condition $0^- \le sup ~\mu _{A}{(x)} + sup ~\sigma _{A}{(x)}+ sup~ \nu _{A}{(x)} \le 3^+$.

Definition 4

(Wang et al. 2010) A single-valued neutrosophic set A in X is characterized by truth-membership function $\mu _{A}{(x)}$, indeterminacy-membership function $\sigma _{A}{(x)}$ and falsity-membership function $\nu _{A}{(x)}$, such that $\mu _{A}{(x)}$, $\sigma _{A}{(x)}$, $\nu _{A}{(x)} \in [0,1]$, $\forall ~x~ \in X$. This is written as $\tilde{A}=\left\{ \mu _{A}{(x)},\sigma _{A}{(x)},\nu _{A}{(x)}:x\in X\right\}$ and satisfies the condition $0 \le sup ~\mu _{A}{(x)} + sup ~\sigma _{A}{(x)}+ sup~ \nu _{A}{(x)} \le 3$.

Definition 5

(Wang et al. 2010) Let $\tilde{A}=\big \{\langle (a_1,a_2,a_3);$$w_A,u_A,v_A\big \}$ and $\tilde{B}=\big \{\langle (b_1,b_2,b_3);w_B,u_B,v_B\big \}$ are two single-valued GSTNNs. Then, the set theoretic operations on $\tilde{A}$ and $\tilde{B}$ are as follows:

• (1) Union of GSTNNs:

  $$\begin{aligned} \tilde{A} \cup \tilde{B} =\left\{ \max {(\mu _{A}{(x)},\mu _{{B}}{(x)})},\min {(\sigma _{A}{(x)},\sigma _{{B}}{(x)})},\right. \nonumber \\ \left. \min {(\nu _{A}{(x)},\nu _{{B}}{(x)})}: x\in X\right\} . \end{aligned}$$

• (2) Intersection of GSTNNs:

  $$\begin{aligned} \tilde{A} \cap \tilde{B} =\left\{ \min {(\mu _{A}{(x)},\mu _{{B}}{(x)})},\max {(\sigma _{A}{(x)},\sigma _{{B}}{(x)})},\right. \nonumber \\ \left. \max {(\nu _{A}{(x)},\nu _{{B}}{(x)})}: x\in X\right\} . \end{aligned}$$

• (3) Product of GSTNN by constant:

  $$\begin{aligned} \gamma \tilde{A}= {\left\{ \begin{array}{ll} \langle (\gamma a_1,\gamma a_2,\gamma a_3);w_A, u_A, v_A \rangle &{} \gamma \ge 0 \\ \langle (\gamma a_3,\gamma a_2,\gamma a_1);w_A, u_A, v_A\rangle &{} \text{( }\gamma <0). \end{array}\right. } \end{aligned}$$

• (4) Multiplication of GSTNNs:

  $$\begin{aligned} \tilde{A}.\tilde{B}= {\left\{ \begin{array}{ll} \langle (a_1b_1,a_2b_2,a_3b_3);w_A \wedge w_B, u_A\vee u_B, v_A\vee v_B \rangle &{} \text{( }a_3>0, b_3>0) \\ \langle (a_1b_3,a_2b_2,a_3b_1);w_A \wedge w_B, u_A\vee u_B, v_A\vee v_B\rangle &{} \text{( }a_3<0,b_3>0) \\ \langle (a_3b_3,a_2b_2,a_1b_1);w_A \wedge w_B, u_A\vee u_B, v_A\vee v_B\rangle &{} \text{( }a_3<0,b_3<0). \end{array}\right. } \end{aligned}$$

• (5) Division of GSTNNs:

  $$\begin{aligned} \tilde{A}/\tilde{B}= {\left\{ \begin{array}{ll} \langle (a_1/b_3,a_2/b_2,a_3/b_1);w_A \wedge w_B, u_A\vee u_B, v_A\vee v_B \rangle &{} \text{( }a_3>0, b_3>0) \\ \langle (a_3/b_3,a_2/b_2,a_1/b_1);w_A \wedge w_B, u_A\vee u_B, v_A\vee v_B\rangle &{} \text{( }a_3<0,b_3>0) \\ \langle (a_3/b_1,a_2/b_2,a_1/b_3);w_A \wedge w_B, u_A\vee u_B, v_A\vee v_B\rangle &{} \text{( }a_3<0,b_3<0). \end{array}\right. } \end{aligned}$$

Appendix B

Proof

Subject to specified N-norm, DM presents any value to the WAM parameter $\rho \in [0,~1]$. Then, the $TAC^N(t_1,\rho )$ function of model (22) reduces to a single variable function $TAC^N(t_1)$ for given $\rho \in [0,~1]$.

In order to find out minimum $TAC^N(t_1)$, the first-order derivative of $TAC^N(t_1)$ with respect to decision variable $t_1$ is computed as follows:

$$\begin{aligned} \frac{\mathrm{d}TAC^N(t_1)}{\mathrm{d}t_1}= & {} \frac{L}{T(1+\eta e^{-\xi t_1})}\Bigg [\big (C_1^N{(1-\rho ) }+C_1^N\rho \big )e^{\alpha _{0} t_1^{\beta _{0}}}\int _{0}^{t_1}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t\nonumber \\&-\frac{(\big (C_2^N{(1-\rho ) }+C_2^N\rho \big )+\big (C_4^N{(1-\rho ) }+C_4^N\rho \big )\delta )(T-t_1)}{1+\delta (T-t_1)}+\big (C_3^N{(1-\rho ) }+C_3^N\rho \big )(e^{\alpha _{0} t_1^{\beta _{0}}}-1)\nonumber \\ {}+ & {} c\big (I_p^N{(1-\rho ) }+I_p^N\rho \big )e^{\alpha _{0} t_1^{\beta _{0}}}\int _{\sigma }^{t_1}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t\Bigg ]. \end{aligned}$$

(30)

Again, the second-order derivative to $TAC^N(t_1)$ with respect to $t_1$ is obtained as follows:

$$\begin{aligned}&\frac{\mathrm{d}^2TAC^N(t_1)}{\mathrm{d}t_1^2} =\frac{L}{T(1+\eta e^{-\xi t_1})}\Bigg [\big (C_1^N{(1-\rho ) }+C_1^N\rho \big )\nonumber \\&\bigg (1+\alpha _{0}\beta _{0} t_1^{\beta _{0}-1}e^{\alpha _{0} t_1^{\beta _{0}}}\int _{0}^{t_1}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t \bigg )\nonumber \\&+\frac{(\big (C_2^N{(1-\rho ) }+C_2^N\rho \big )+\big (C_4^N{(1-\rho ) }+C_4^N\rho \big )\delta )}{(1+\delta (T-t_1))^2}\nonumber \\&+\big (C_3^N{(1-\rho ) }+C_3^N\rho \big )\alpha _{0} \beta _{0} t_1^{\beta _{0}-1}e^{\alpha _{0} t_1^{\beta _{0}}} \nonumber \\&+c\big (I_p^N{(1-\rho ) }+I_p^N\rho \big )\bigg (1+\alpha _{0}\beta _{0} t_1^{\beta _{0}-1}e^{\alpha _{0} t_1^{\beta _{0}}} \int _{\sigma }^{t_1}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t\bigg )\Bigg ].\nonumber \\ \end{aligned}$$

(31)

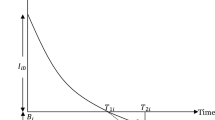
This is to observe that $\rho \in [0,~1]$ and so all the terms in above expression (31) are positive. Therefore, the expression of $\frac{\mathrm{d}^2TAC^N(t_1)}{\mathrm{d}t_1^2}$ is strictly greater than zero $\forall ~ t_1 \ge 0$. Hence, the TAC function is strictly convex $\forall ~ t_1 \ge 0$. Again, by using the necessary condition of optimality in crisp environment (see, for necessary condition, Khanra et al. 2011), the critical point $t_1^*$ can be determined from the following implicit equation

$$\begin{aligned}&\big (C_1^N{(1-\rho ) }+C_1^N\rho \big )e^{\alpha _{0} t_1^{*\beta _{0}}}\int _{0}^{t_1^*}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t-\frac{(\big (C_2^N{(1-\rho ) }+C_2^N\rho \big )+\big (C_4^N{(1-\rho ) }+C_4^N\rho \big )\delta )(T-t_1^*)}{1+\delta (T-t_1^*)}\nonumber \\ {}+ & {} \big (C_3^N{(1-\rho ) }+C_3^N\rho \big )(e^{\alpha _{0} t_1^{*\beta _{0}}}-1)+c\big (I_p^N{(1-\rho ) }+I_p^N\rho \big )e^{\alpha _{0} t_1^{*\beta _{0}}}\int _{\sigma }^{t_1^*}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t=0. \end{aligned}$$

(32)

Since for given $\rho \in [0,~1]$, the TAC function is strictly convex $\forall ~ t_1 \ge 0$, Eq. (32) yields the optimal inventory depletion time $t_1^*$ and thereby the optimal $TAC^{N*}(t_1^*, \rho )$. This way, subject to specified N-norm, the sufficient condition of optimality of $TAC^{N}(t_1, \rho )$ is satisfied for given $\rho \in [0,~1]$. This completes the proof.

Appendix C

Proof

Subject to specified N-norm, DM presents any value to the WAM parameter $\rho \in [0,~1]$. Then, the $TAC^N(t_1,\rho )$ function reduces to a single variable function $TAC^N(t_1)$ for given $\rho \in [0,~1]$. In order to find out minimum $TAC^N(t_1)$, the first order derivative of $TAC^N(t_1)$ with respect to decision variable $t_1$ is computed as follows:

$$\begin{aligned} \frac{\mathrm{d}TAC^N(t_1)}{\mathrm{d}t_1}= & {} \frac{1}{T}\Bigg [\frac{L}{(1+\eta e^{-\xi t_1})}\bigg \{\big (C_1^N{(1-\rho ) }+C_1^N\rho \big )e^{\alpha _{0} t_1^{\beta _{0}}}\int _{0}^{t_1}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t\nonumber \\&-\frac{(\big (C_2^N{(1-\rho ) }+C_2^N\rho \big )+\big (C_4^N{(1-\rho ) }+C_4^N\rho \big )(\rho )\delta )(T-t_1)}{1+\delta (T-t_1)}+\big (C_3^N{(1-\rho ) }+C_3^N\rho \big )(e^{\alpha _{0} t_1^{\beta _{0}}}-1)\nonumber \\ {}- & {} p\big (I_e^N{(1-\rho ) }+I_e^N\rho \big )\sigma \bigg \}+p\big (I_e^N{(1-\rho ) }+I_e^N\rho \big )\int _{0}^{t_1}\frac{L}{1+\eta e^{-\xi t_1}}\mathrm{d}t\Bigg ]. \end{aligned}$$

(33)

Again, the second-order derivative to $TAC^N(t_1)$ with respect to $t_1$ is obtained as follows:

$$\begin{aligned} \frac{\mathrm{d}^2TAC^N(t_1)}{\mathrm{d}t_1^2}= & {} \frac{L}{T(1+\eta e^{-\xi t_1})}\Bigg [\big (C_1^N{(1-\rho ) }+C_1^N\rho \big )\bigg (1+\alpha _{0}\beta _{0} t_1^{\beta _{0}-1}e^{\alpha _{0} t_1^{\beta _{0}}}\int _{0}^{t_1}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t \bigg )\nonumber \\ {}+ & {} \frac{(\big (C_2^N{(1-\rho ) }+C_2^N\rho \big )+\big (C_4^N{(1-\rho ) }+C_4^N\rho \big )\delta )}{(1+\delta (T-t_1))^2}+\big (C_3^N{(1-\rho ) }+C_3^N\rho \big )\alpha _{0} \beta _{0} t_1^{\beta _{0}-1}e^{\alpha _{0} t_1^{\beta _{0}}}\nonumber \\ {}+ & {} p\big (I_e^N{(1-\rho ) }+I_e^N\rho \big )\Big \{1-\eta \xi e^{-\xi t_1}\int _{0}^{t_1}\frac{1}{1+\eta e^{-\xi t_1} }\mathrm{d}t\Big \} \Bigg ]. \end{aligned}$$

(34)

This is observed that all the terms in above expression (34) are positive, provided the condition

$\eta \xi e^{-\xi t_1}\int _{0}^{t_1}\frac{1}{1+\eta e^{-\xi t_1} }\mathrm{d}t<1$ is satisfied for any $\rho \in [0,~1]$. So, the expression of $\frac{\mathrm{d}^2TAC^N(t_1)}{\mathrm{d}t_1^2}$ is strictly greater than zero $\forall ~ t_1 \ge 0$, provided $\eta \xi e^{-\xi t_1}\int _{0}^{t_1}\frac{1}{1+\eta e^{-\xi t_1} }\mathrm{d}t<1$, showing the TAC function to be strictly convex $\forall ~ t_1 \ge 0$. Again, by using the necessary condition of optimality in crisp environment (see, for necessary condition, Khanra et al. 2011), the critical point $t_1^*$ can be determined from the following implicit equation

$$\begin{aligned}&\frac{L}{(1+\eta e^{-\xi t_1^*})}\bigg \{\big (C_1^N{(1-\rho ) }+C_1^N\rho \big )e^{\alpha _{0} t_1^{*\beta _{0}}}\int _{0}^{t_1^*}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t-\frac{(\big (C_2^N{(1-\rho ) }+C_2^N\rho \big )+\big (C_4^N{(1-\rho ) }+C_4^N\rho \big )\delta )(T-t_1^*)}{1+\delta (T-t_1^*)}\nonumber \\ {}+ & {} \big (C_3^N{(1-\rho ) }+C_3^N\rho \big )(e^{\alpha _{0} t_1^{*\beta _{0}}}-1)-p\big (I_e^N{(1-\rho ) }+I_e^N\rho \big )\sigma \bigg \}+p\big (I_e^N{(1-\rho ) }+I_e^N\rho \big )\int _{0}^{t_1^*}\frac{L}{1+\eta e^{-\xi t_1^*}}\mathrm{d}t=0. \end{aligned}$$

(35)

Since for given $\rho \in [0,~1]$, the TAC function is strictly convex $\forall ~ t_1 \ge 0$, provided $\eta \xi e^{-\xi t_1}\int _{0}^{t_1}\frac{1}{1+\eta e^{-\xi t_1} }\mathrm{d}t<1$; Eq. (35) yields the optimal inventory depletion time $t_1^*$ and thereby the optimal $TAC^{N*}(t_1^*, \rho )$. This way, subject to specified N-norm, the sufficient condition of optimality of $TAC^{N}$ is satisfied subject to the condition $\eta \xi e^{-\xi t_1}\int _{0}^{t_1}\frac{1}{1+\eta e^{-\xi t_1} }\mathrm{d}t<1$ for given $\rho \in [0,~1]$. This completes the proof.

Appendix D

Proof

Let $A=[a_1,a_2]$, $0<a_1<a_2$ be a closed and bounded interval with weights $w_1, w_2$. Since any interval number can be well represented by a function, one gets the WAM as follows:

$$\begin{aligned} WAM_A(\rho )= & {} \frac{w_1a_1+w_2a_2}{w_1+w_2},~~w_1>0,w_2>0\\= & {} a_1{(1-\rho ) }+a_2\rho ,\text {where}~\rho =\frac{w_2}{w_1+w_2} \in [0,1]. \end{aligned}$$

The choice of parameter $\rho$ reflects some attitude on part of DM (Kheiri and Cao 2016). Again, the function $WAM_A(\rho )=a_1{(1-\rho ) }+a_2\rho ,~\rho \in [0,1]$ is strictly monotone (increasing) and continuous function. Now, since sum of two continuous function is also a continuous function and $\frac{d(WAM_A(\rho ))}{\mathrm{d}\rho }=a_2-a_1 > 0~\text {for}~\rho \in [0,1]$, the polynomial function $WAM_A(\rho ) = a_1{(1-\rho ) }+a_2\rho$, is continuous function for $a_1,a_2>0$. Hence, this shows that $WAM_A(\rho )$ is monotonically increasing continuous function. This completes the proof.

Appendix E

Proof

Subject to NC-norm, DM presents any value to the WAM parameter $\rho \in [0,~1]$. Then, the $TAC^{NC}(t_1,\rho )$ function reduces to a single variable function $TAC^{NC}(t_1)$ for given $\rho \in [0,~1]$. In order to find out minimum $TAC^{NC}(t_1)$, the first order derivative of $TAC^{NC}(t_1)$ with respect to decision variable $t_1$ is computed as follows:

$$\begin{aligned} \frac{\mathrm{d}TAC^{NC}(t_1)}{\mathrm{d}t_1}= & {} \frac{L}{T(1+\eta e^{-\xi t_1})}\Bigg [C^{NC}_1(\rho )e^{\alpha _{0} t_1^{\beta _{0}}}\int _{0}^{t_1}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t-\frac{(C^{NC}_2(\rho )+C^{NC}_4(\rho )\big )\delta )(T-t_1)}{1+\delta (T-t_1)}\nonumber \\&+C^{NC}_3(\rho )(e^{\alpha _{0} t_1^{\beta _{0}}}-1)+cI^{NC}_p(\rho )e^{\alpha _{0} t_1^{\beta _{0}}}\int _{\sigma }^{t_1}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t\Bigg ]. \end{aligned}$$

(36)

Again, the second-order derivative to $TAC^{NC}(t_1)$ with respect to $t_1$ is obtained as follows:

$$\begin{aligned}&\frac{\mathrm{d}^2TAC^{NC}(t_1)}{\mathrm{d}t_1^2}=\frac{L}{T(1+\eta e^{-\xi t_1})}\nonumber \\&\Bigg [C^{NC}_1(\rho )\bigg (1+\alpha _{0}\beta _{0} t_1^{\beta _{0}-1}e^{\alpha _{0} t_1^{\beta _{0}}}\int _{0}^{t_1}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t \bigg )\nonumber \\&+\frac{(C^{NC}_2(\rho )+C^{NC}_4(\rho )\delta )}{(1+\delta (T-t_1))^2} +C^{NC}_3(\rho )\alpha _{0} \beta _{0} t_1^{\beta _{0}-1}e^{\alpha _{0} t_1^{\beta _{0}}}\nonumber \\&+cI^{NC}_p(\rho )\bigg (1+\alpha _{0}\beta _{0} t_1^{\beta _{0}-1}e^{\alpha _{0} t_1^{\beta _{0}}} \int _{\sigma }^{t_1}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t\bigg )\Bigg ]. \end{aligned}$$

(37)

This is to observe that $\rho \in [0,~1]$ and so all the terms in above expression (37) are positive. Therefore, the expression of $\frac{\mathrm{d}^2TAC^N(t_1)}{\mathrm{d}t_1^2}$ is strictly greater than zero $\forall ~ t_1 \ge 0$. Hence, the TAC function is strictly convex $\forall ~ t_1 \ge 0$. Again, by using the necessary condition of optimality in crisp environment (see, for necessary condition, Khanra et al. 2011), the critical point $t_1^*$ can be determined from the following implicit equation

$$\begin{aligned}&C^{NC}_1(\rho )e^{\alpha _{0} t_1^{*\beta _{0}}}\int _{0}^{t_1^*}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t\nonumber \\&{-}\frac{(C^{NC}_2(\rho )+C^{NC}_4(\rho )\big )\delta )(T-t_1^*)}{1+\delta (T-t_1^*)}+C^{NC}_3(\rho )(e^{\alpha _{0} t_1^{*\beta _{0}}}-1)\nonumber \\&{+}cI^{NC}_p(\rho )e^{\alpha _{0} t_1^{*\beta _{0}}}\int _{\sigma }^{t_1^*}e^{-\alpha _{0} t^{\beta _{0}}}\mathrm{d}t=0. \end{aligned}$$

(38)

Since for given $\rho \in [0,~1]$, the TAC function is strictly convex $\forall ~ t_1 \ge 0$, Eq. (38) yields the optimal inventory depletion time $t_1^*$ and thereby the optimal $TAC^{NC*}(t_1^*, \rho )$. This way, subject to specified NC-norm, the sufficient condition of optimality of $TAC^{NC}(t_1, \rho )$ is satisfied for given $\rho \in [0,~1]$. This completes the proof.