Pricing mode selection for the online short video platform

Abstract

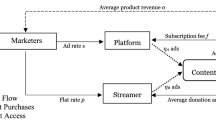
Online short video platform usually adopts advertising mode and mixed mode as the pricing mode. How to choose the optimal pricing mode for the online short video platform is a topic worthy of our attention. This paper discusses the pricing mode that should be adopted by the online short video platform and investigates the effects of the viewer’s nuisance cost and cross-network externality intensity on the pricing mode selection of short video platform. The results show that, when the viewer’s nuisance cost is low and the intensity of cross-network externality is high, the platform should choose the advertising mode; otherwise, it should choose the mixed mode; when the cost is high and the intensity is low, the advertising price under the advertising mode is higher than that under the mixed mode; otherwise, the advertising price under the advertising mode is lower than that under the mixed mode; when the cost is relatively low and regardless of the intensity, the payment cost under the mixed mode is higher than that under the advertising mode; otherwise, the payment cost under the mixed mode is lower than that under the mixed mode. Importantly, we also find that, under certain conditions, interests of online short video platform and video content providers may be inconsistent.

Appendix

Proof of Lemma 1

The first-order condition of Eq. (6a) with respect to $p_{s}^{A}$ is $\frac{{\partial \Pi^ {A} (p_{a}^{A} ,p_{s}^{A} )}}{{\partial {\kern 1pt} p_{s}^{A} }} = - \frac{{\alpha {\kern 1pt} N(v + \lambda {\kern 1pt} N)}}{{v + \gamma {\kern 1pt} (\beta - p_{a}^{A} )}}$, obviously, $\frac{{\partial \Pi^{A} (p_{a}^{A} ,p_{s}^{A} )}}{{\partial {\kern 1pt} p_{s}^{A} }} < 0$, i.e., $\Pi^{A}$ is the decreasing function of $p_{s}^{A}$, so we can obtain the optimal solution of model (6) at the boundary of $p_{s}^{A}$. By Eq. (6b), let $p_{s}^{A} {\kern 1pt} \alpha \frac{{v + \lambda {\kern 1pt} N}}{{v + \gamma {\kern 1pt} (\beta - p_{a}^{A} )}} - c_{s} = 0$,

$$ p_{s}^{*} = \frac{{c_{s} \left[{v + \gamma {\kern 1pt} {\kern 1pt} (\beta - p_{a}^{A} )} \right]}}{{\alpha (v + \lambda {\kern 1pt} N)}} . $$

(A.1)

Substituting Eq. (A.1) into Eq. (6a), we obtain

$$ \Pi^{A} (p_{a}^{A} ) = \frac{{p_{a}^{A} (\beta - p_{a}^{A} )(v + \lambda {\kern 1pt} N)^{2} }}{{\left[{v + \gamma {\kern 1pt} {\kern 1pt} (\beta - p_{a}^{A} )} \right]{\kern 1pt}^{2} }} - N{\kern 1pt} c_{s} . $$

(A.2)

The first-order condition of Eq. (A.2) with respect to $p_{a}^{A}$is $\frac{{\partial \Pi^{A} }}{{\partial {\kern 1pt} p_{a}^{A} }} = \frac{{(v + \lambda {\kern 1pt} N)^{2} (\beta {\kern 1pt} v - 2p_{a}^{A} {\kern 1pt} v + \beta^{2} \gamma - \beta {\kern 1pt} \gamma {\kern 1pt} p_{a}^{A} )}}{{(v + \beta {\kern 1pt} \gamma - \gamma {\kern 1pt} p_{a}^{A} )^{3} }}$; furthermore, the second-order condition of Eq. (A.2) with $p_{a}^{A}$ is

$$ \frac{{\partial^{2} \Pi^{A} }}{{\partial (p_{a}^{A} )^{2} }} = - \frac{{2(v + \lambda N)^{2} (v^{2} - \beta^{2} \gamma^{2} + 2\gamma p_{a}^{A} v + \beta \gamma^{2} p_{a}^{A} )}}{{(v + \beta \gamma - \gamma p_{a}^{A} )^{4} }} . $$

(A.3)

Let $\frac{{\partial \Pi^{A} }}{{\partial p_{a}^{A} }} = 0$, we can obtain $p_{a}^{A*} = \frac{{\beta {\kern 1pt} (v + \beta {\kern 1pt} \gamma )}}{{2v + \beta {\kern 1pt} \gamma }}$. Substituting $p_{a}^{A*}$ into Eq. (A.3), we can obtain $\frac{{\partial^{2} \Pi^{A} }}{{\partial (p_{a}^{A} )^{2} }} = - \frac{{(2v + \beta {\kern 1pt} \gamma )^{4} (v + \lambda {\kern 1pt} N)^{2} }}{{8v^{3} (v + \beta {\kern 1pt} \gamma )^{3} }}$, obviously, $\frac{{\partial^{2} \Pi^{A} }}{{\partial (p_{a}^{A} )^{2} }} < 0$. Therefore, $p_{a}^{A*}$ is the optimal solution of model (6).

Furthermore, substituting $p_{a}^{A*}$ into Eq. (A.1), we can obtain $p_{s}^{A*} = \frac{{2c_{s} v{\kern 1pt} (v + \beta {\kern 1pt} \gamma )}}{{\alpha (2v + \beta {\kern 1pt} \gamma )(v + \lambda {\kern 1pt} N)}}$.

Therefore, Lemma 1 holds.

Proof of Corollary 1

(i) The first-order conditions of Eq. (9) with respect to $N$, $\gamma$, $\beta$ and $\lambda$ are $\frac{{\partial n_{u}^{A*} }}{\partial N} = \frac{{\lambda {\kern 1pt} {\kern 1pt} (2v + \beta {\kern 1pt} \gamma )}}{{2v(v + \beta {\kern 1pt} \gamma )}}$,$\frac{{\partial n_{u}^{A*} }}{\partial \gamma } = - \frac{{\beta (v + \lambda {\kern 1pt} N)}}{{2(v + \beta {\kern 1pt} \gamma )^{2} }}$, $\frac{{\partial n_{u}^{A*} }}{\partial \beta } = - \frac{{\gamma {\kern 1pt} (v + \lambda {\kern 1pt} N)}}{{2(v + \beta {\kern 1pt} \gamma )^{2} }}$, $\frac{{\partial n_{u}^{A*} }}{\partial \lambda } = \frac{{N(2v + \beta {\kern 1pt} \gamma )}}{{2v{\kern 1pt} (v + \beta {\kern 1pt} \gamma )}}$, respectively. Obviously, we know $\frac{{\partial n_{u}^{A*} }}{\partial N} > 0$, $\frac{{\partial n_{u}^{A*} }}{\partial \gamma } < 0$, $\frac{{\partial n_{u}^{A*} }}{\partial \beta } < 0$, $\frac{{\partial n_{u}^{A*} }}{\partial \lambda } > 0$.

(ii) The first-order conditions of Eq. (10) with respect to $N$, $\gamma$, $\beta$ and $\lambda$ are $\frac{{\partial n_{a}^{A*} }}{\partial N} = \frac{{\lambda {\kern 1pt} \beta }}{{2{\kern 1pt} (v + \beta {\kern 1pt} \gamma )}}$, $\frac{{\partial n_{a}^{A*} }}{\partial \gamma } = - \frac{{\beta^{2} (v + \lambda {\kern 1pt} N)}}{{2(v + \beta {\kern 1pt} \gamma )^{2} }}$, $\frac{{\partial n_{a}^{A*} }}{\partial \beta } = \frac{{v{\kern 1pt} {\kern 1pt} (v + \lambda {\kern 1pt} N)}}{{2(v + \beta {\kern 1pt} \gamma )^{2} }}$, $\frac{{\partial n_{a}^{A*} }}{\partial \lambda } = \frac{{\beta {\kern 1pt} N}}{{2(v + \beta {\kern 1pt} \gamma )}}$, respectively. Obviously, we know $\frac{{\partial n_{a}^{A*} }}{\partial N} > 0$, $\frac{{\partial n_{a}^{A*} }}{\partial \gamma } < 0$, $\frac{{\partial n_{a}^{A*} }}{\partial \beta } > 0$, $\frac{{\partial n_{a}^{A*} }}{\partial \lambda } > 0$.

Therefore, Corollary 1 holds.

Proof of Corollary 2

(i) The first-order conditions of Eq. (7) with respect to $\gamma$ and $\beta$ are $\frac{{\partial p_{a}^{A*} }}{\partial \gamma } = \frac{{\beta^{2} v}}{{(2v + \beta {\kern 1pt} \gamma )^{2} }}$, $\frac{{\partial p_{a}^{A*} }}{\partial \beta } = \frac{{\beta^{2} \gamma^{2} + 2v^{2} + 4\beta {\kern 1pt} \gamma {\kern 1pt} {\kern 1pt} v}}{{(2v + \beta {\kern 1pt} \gamma )^{2} }}$, respectively. Obviously, $\beta \gamma \frac{{\partial p_{a}^{A*} }}{\partial \gamma } > 0$, $\frac{{\partial p_{a}^{A*} }}{\partial \beta } > 0$.

(ii) The first-order conditions of Eq. (8) with respect to$N$, γ, β and $\lambda$ are $\frac{{\partial p_{s}^{A*} }}{\partial N} = - \frac{{2\lambda {\kern 1pt} c_{s} v(v + \beta {\kern 1pt} \gamma )}}{{\alpha (2{\kern 1pt} {\kern 1pt} v + \beta {\kern 1pt} \gamma )(v + \lambda {\kern 1pt} N)}}$, $\frac{{\partial p_{s}^{A*} }}{\partial \gamma } = \frac{{2\beta {\kern 1pt} c_{s} v^{2} }}{{\alpha (2v + \beta {\kern 1pt} \gamma )^{2} (v + \lambda {\kern 1pt} N)}}$, $\frac{{\partial p_{s}^{A*} }}{\partial \beta } = \frac{{2{\kern 1pt} c_{s} {\kern 1pt} \gamma {\kern 1pt} {\kern 1pt} v^{2} }}{{\alpha (2v + \beta {\kern 1pt} \gamma )^{2} (v + \lambda {\kern 1pt} N)}}$, $\frac{{\partial p_{s}^{A*} }}{\partial \lambda } = - \frac{{2c_{s} v{\kern 1pt} N(v + \beta {\kern 1pt} {\kern 1pt} \gamma )}}{{\alpha (2v + \beta {\kern 1pt} \gamma )(v + \lambda {\kern 1pt} N)^{2} }}$, respectively. Obviously, $\frac{{\partial p_{s}^{A*} }}{\partial N} < 0$, $\frac{{\partial p_{s}^{A*} }}{\partial \gamma } > 0$, $\frac{{\partial p_{s}^{A*} }}{\partial \beta } > 0$, $\frac{{\partial p_{s}^{A*} }}{\partial \lambda } < 0$.

(iii) The first-order condition of Eq. (11) with respect to $N$is $\frac{{\partial \Pi^{A*} }}{\partial N} = \frac{{\beta^{2} \lambda (v + \lambda {\kern 1pt} N) - 2v{\kern 1pt} c_{s} (v + \beta {\kern 1pt} \gamma )}}{{2v(v + \beta {\kern 1pt} \gamma )}}$. When $\beta^{2} \lambda (v + \lambda {\kern 1pt} N) - 2v{\kern 1pt} (v + \beta {\kern 1pt} \gamma )c_{s} > 0$, i.e., $N > N_{0} = \frac{{v{\kern 1pt} {\kern 1pt} (2c_{s} {\kern 1pt} v - \lambda {\kern 1pt} \beta^{2} + 2\beta {\kern 1pt} \gamma {\kern 1pt} c_{s} )}}{{\lambda^{2} {\kern 1pt} \beta^{2} }}$, we know $\frac{{\partial \Pi^{A*} }}{\partial N} > 0$. When $N < N_{0}$, $\frac{{\partial \Pi^{A*} }}{\partial N} < 0$. Furthermore, the first-order conditions of Eq. (11) with respect to $\gamma$, $\beta$ and $\lambda$ are $\frac{{\partial \Pi^{A*} }}{\partial \gamma } = - \frac{{\beta^{3} (v + \lambda_{u} N)^{2} }}{{4v{\kern 1pt} {\kern 1pt} (v + \beta {\kern 1pt} \gamma )^{2} }}$, $\frac{{\partial \Pi^{A*} }}{\partial \beta } = \frac{{\beta (2{\kern 1pt} v + \beta {\kern 1pt} \gamma )(v + \lambda_{u} N)^{2} }}{{4v(v + \beta {\kern 1pt} \gamma )^{2} }}$, $\frac{{\partial \Pi^{A*} }}{\partial \lambda } = \frac{{\beta^{2} N(v + \lambda {\kern 1pt} N)}}{{2v(v + \beta {\kern 1pt} \gamma )}}$, respectively. Obviously, $\frac{{\partial \Pi^{A*} }}{\partial \gamma } < 0$, $\frac{{\partial \Pi^{A*} }}{\partial \beta } > 0$, $\frac{{\partial \Pi^{A*} }}{\partial \lambda } > 0$.

Hence, Corollary 2 holds.

Proof of Lemma 2

The first-order condition of Eq. (23a) with respect to $p_{s}^{M}$ is$\frac{{\partial \Pi^{M} (p_{a}^{M} ,p_{u}^{M} ,p_{s}^{M} )}}{{\partial p_{s}^{M} }} = - N\alpha \frac{{(1 - k)(k{\kern 1pt} v + \lambda {\kern 1pt} N)v + \gamma (\beta - p_{a}^{M} )(v + \lambda {\kern 1pt} N) - \gamma {\kern 1pt} p_{u}^{M} (\beta - \gamma )}}{{\left[{(1 - k)k{\kern 1pt} v + \gamma (\beta - p_{a}^{M} )} \right]v}}$; then, we know $\frac{{\partial \Pi (p_{a}^{M} ,p_{u}^{M} ,p_{s}^{M} )}}{{\partial p_{s}^{M} }} < 0$, i.e., $\Pi^{M}$ is the decreasing function of $p_{s}^{M}$, so we can obtain the optimal solution of model (23) at the boundary of $p_{s}^{M}$.

By Eq. (23b), let $p_{s}^{M} \alpha \frac{{(1 - k)(kv + \lambda N)v + \gamma (\beta - p_{a}^{M} )(v + \lambda N) - \gamma p_{u}^{M} (\beta - \gamma )}}{{\left[{(1 - k)kv + \gamma (\beta - p_{a}^{M} )} \right]v}} - c_{s} = 0$, we can obtain

$$ p_{s}^{*} = \frac{{\left[{(1 - k)kv + \gamma (\beta - p_{a}^{M} )} \right]c_{s} v}}{{\left[{(1 - k)(kv + \lambda N)v + \gamma (\beta - p_{a}^{M} )(v + \lambda N) - \gamma p_{u}^{M} (\beta - \gamma )} \right]\alpha }} . $$

(A.4)

Substituting Eq. (A.4) into Eq. (23a), we have

$$ \Pi^{M} (p_{a}^{M} ,p_{u}^{M} ) = \frac{{p_{a}^{M} (\beta - p_{a}^{M} )\left[{kp_{u}^{M} + \lambda N(1 - k)} \right]^{{{\kern 1pt} 2}} }}{{\left[{(1 - k)kv + \gamma (\beta - p_{a}^{M} )} \right]^{{{\kern 1pt} 2}} }} + \frac{{p_{u}^{M} \gamma (\beta - p_{a}^{M} )\left[{kp_{u}^{M} + \lambda N(1 - k)} \right]}}{{\left[{(1 - k)kv + \gamma (\beta - p_{a}^{M} )} \right](1 - k)v}} $$

$$ + \frac{{p_{u}^{M} (v - kv - p_{u}^{M} )}}{(1 - k)v} - Nc_{s} . $$

(A.5)

The first-order conditions of Eq. (A.5) with respect to $p_{a}^{M}$ and $p_{u}^{M}$ are

$\frac{{\partial \Pi^{M} }}{{\partial p_{a}^{M} }} = \frac{{G^{2} \left[{(\beta - 2p_{a}^{M} )W + 2\gamma p_{a}^{M} (\beta - p_{a}^{M} )} \right]}}{{W^{3} }} + \frac{{\gamma p_{u}^{M} \left[{\gamma (\beta - p_{a}^{M} )G - W} \right]}}{{W^{2} (1 - k)v}},$ $\frac{{\partial \Pi^{M} }}{{\partial p_{u}^{M} }} = \frac{{kp_{a}^{M} (\beta - p_{a}^{M} )}}{{W^{2} }} + \frac{{\left[{2k\gamma (\beta - p_{a}^{M} )p_{u}^{M} + \lambda N\gamma (1 - k)(\beta - p_{a}^{M} )} \right]}}{W(1 - k)v} + \frac{{(1 - k)v - 2p_{u}^{M} }}{(1 - k)v},$

where $W = (1 - k)kv + \gamma (\beta - p_{a}^{M} )$, $G = kp_{u}^{M} + \lambda N(1 - k)$. Furthermore, the second-order conditions with respect to $p_{a}^{M}$and $p_{u}^{M}$ are

$$ \frac{{\partial^{2} \Pi^{M} }}{{\partial (p_{a}^{M} )^{2} }}\, = \frac{{G^{2} \left[{\beta \gamma - 2\gamma p_{a}^{M} - 2W} \right]W + 3G^{2} \gamma \left[{(\beta - 2p_{a}^{M} )W + 2\gamma p_{a}^{M} (\beta - p_{a}^{M} )} \right]}}{{W^{4} }} $$

$$ + \frac{{2\gamma^{2} p_{u}^{M} \left[{\gamma (\beta - p_{a}^{M} ) - 2W} \right]}}{{W^{3} (1 - k)v}} , $$

(A.6)

$$ \frac{{\partial^{2} \Pi^{M} }}{{\partial p_{u}^{M} \partial p_{a}^{M} }} = \frac{{(k\beta - 2kp_{a}^{M} )W + 2k\gamma p_{a}^{M} (\beta - p_{a}^{M} )}}{{W^{3} }} + \frac{{\left[{2k\gamma p_{u}^{M} + \lambda \gamma N(1 - k)} \right]\left[{\gamma (\beta - p_{a}^{M} ) + W} \right]}}{{W^{2} (1 - k)v}}, $$

(A.7)

$$ \frac{{\partial^{2} \Pi^{M} }}{{\partial (p_{u}^{M} )^{2} }}{\kern 1pt} = \frac{{2k\gamma (\beta - p_{a}^{M} ) - 2W}}{W(1 - k)v}. $$

(A.8)

Let $\frac{{\partial \Pi^{M} }}{{\partial p_{a}^{M} }} = 0$ and $\frac{{\partial \Pi^{M} }}{{\partial p_{u}^{M} }} = 0$, and we can get

$$ p_{a}^{M*} = \frac{{(\beta - \gamma )kv\left[{kv(1 - k) + \beta \gamma } \right] + \lambda \beta N\left[{2kv(1 - k) - k\gamma (\beta + \gamma ) - 2\beta \gamma } \right]}}{{(kv + \lambda N)\left[{\beta \gamma + 2kv(1 - k)} \right] + (\beta \gamma + 2kv)(1 - k)\lambda N}}, $$

$$ p_{u}^{M*} = \frac{{(1 - k)\left[{2kv(1 - k) + 2\beta \gamma v + \lambda \beta N(\beta + \gamma )} \right]}}{{4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k}}. $$

Substituting $p_{a}^{M*}$and $p_{u}^{M*}$ into Eqs. (A.6), (A.7) and (A.8), respectively. Through the analysis, we can find $\frac{{\partial^{2} \Pi^{M} }}{{\partial (p_{a}^{M} )^{2} }} < 0$, $\frac{{\partial^{2} \Pi^{M} }}{{\partial (p_{u}^{M} )^{2} }} < 0$, and $\frac{{\partial^{2} \Pi^{M} }}{{\partial (p_{a}^{M} )^{2} }} \cdot \frac{{\partial^{2} \Pi^{M} }}{{\partial (p_{u}^{M} )^{2} }} - \left({\frac{{\partial^{2} \Pi^{M} }}{{\partial p_{u}^{M} \partial p_{a}^{M} }}} \right)^{2} > 0$when $4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k > 0$. Therefore, $p_{a}^{M*}$ and $p_{u}^{M*}$ are the optimal solutions of model (23).

Substituting $p_{a}^{M*}$ and $p_{u}^{M*}$ into Eq. (A.4), we have $p_{s}^{M*} = \frac{{c_{s} {\kern 1pt} k{\kern 1pt} v\left[{4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k} \right]}}{{\alpha \left[{4kv(1 - k)(kv + \lambda N) - (\beta + \gamma )(\beta \,k\,v + \lambda \,\beta {\kern 1pt} N + \lambda {\kern 1pt} \gamma {\kern 1pt} N) + 2\beta {\kern 1pt} \gamma {\kern 1pt} \lambda {\kern 1pt} N(1 + k) - \gamma^{2} kv + 3\beta {\kern 1pt} \gamma N {\kern 1pt} k{\kern 1pt} v} \right]}}$.

Hence, Lemma 2 holds.

Proof of Corollary 3

(i) The first-order conditions of Eq. (29) with respect to N and $\lambda$ are

$\frac{{\partial n_{u}^{M*} }}{\partial N} = \frac{{\lambda \left[{4kv(1 - k) + 2\beta \gamma - \beta^{2} k - \gamma^{2} k} \right]}}{{\left[{4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k} \right]kv}}$and $\frac{{\partial n_{u}^{M*} }}{\partial \lambda } = \frac{{N\left[{4kv(1 - k) + 2\beta \gamma - \beta^{2} k - \gamma^{2} k} \right]}}{{\left[{4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k} \right]kv}}$, respectively. Because $4kv(1 - k) + 2\beta \gamma - \beta^{2} k - \gamma^{2} k > 4kv(1 - k) + 2\beta \gamma - (\beta^{2} + \gamma^{2} )k > 0$, we have $\frac{{\partial n_{u}^{M*} }}{\partial N} > 0$ and $\frac{{\partial n_{u}^{M*} }}{\partial \lambda } > 0$.

(ii) The first-order conditions of Eq. (30) with respect to $N$ and $\lambda$ are $\frac{{\partial n_{a}^{M*} }}{\partial N} = \frac{2\lambda \beta (1 - k)}{{4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k}}$ and $\frac{{\partial n_{a}^{M*} }}{\partial \lambda } = \frac{2\beta N(1 - k)}{{4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k}}$, respectively. Obviously, $\frac{{\partial n_{a}^{M*} }}{\partial N} > 0$, $\frac{{\partial n_{a}^{M*} }}{\partial \lambda } > 0$.

Hence, Corollary 3 holds.

Proof of Corollary 4

(i) The first-order conditions of Eq. (24) with respect to $N$ and $\lambda$ are

$\frac{{\partial p_{a}^{M*} }}{\partial N} = \frac{{\lambda \gamma k^{2} v^{2} (1 - k)\left[{4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k} \right]}}{{\left[{(kv + \lambda N)(\beta \gamma + 2kv - 2k^{2} v) + (\beta \gamma + 2kv)(1 - k)\lambda N} \right]{\kern 1pt}^{2} }},$ $\frac{{\partial p_{a}^{M*} }}{\partial \lambda } = \frac{{N\gamma k^{2} v^{2} (1 - k)\left[{4\frac{{\partial p_{a}^{M*} }}{\partial N} > 0 kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k} \right]}}{{\left[{(kv + \lambda N)(\beta \gamma + 2kv - 2k^{2} v) + (\beta \gamma + 2kv)(1 - k)\lambda N} \right]{\kern 1pt}^{2} }}.$

Similar to the proof of Corollary 3(i), we have $\frac{{\partial p_{a}^{M*} }}{\partial N} > 0$ and $\frac{{\partial p_{a}^{M*} }}{\partial \lambda } > 0$.

The first-order condition of Eq. (24) with respect to $\gamma$ is

$$ \begin{aligned} \frac{{\partial p_{a}^{M*} }}{\partial \gamma } = & kv(1 - k)\frac{{2(1 - k)(k^{3} v^{3} - \lambda^{2} \beta^{2} N^{2} ) - (\beta - \gamma )^{2} k^{2} v^{2} + 2\beta \lambda^{2} N^{2} (2k\gamma - \beta )}}{{\left[ {(kv + \lambda N)(\beta \gamma + 2kv - 2k^{2} v) + (\beta \gamma + 2kv)(1 - k)\lambda N} \right]{\kern 1pt}^{2} }} \\ & \; + kv(1 - k)\frac{{\lambda Nkv\left[ {4kv(1 - k) + 4\gamma (\gamma - \beta ) + (\beta + \gamma )^{2} k} \right]}}{{\left[ {(kv + \lambda N)(\beta \gamma + 2kv - 2k^{2} v) + (\beta \gamma + 2kv)(1 - k)\lambda N} \right]{\kern 1pt}^{2} }}, \\ \end{aligned} $$

when $\gamma < \gamma_{0} = \frac{{\sqrt {2(kv + 2\lambda N)(v + \lambda N)W} + 2\lambda \beta N(v - \lambda N) + \beta kv(v + \lambda N)}}{kv(v + \lambda N)}$, we know $\frac{{\partial p_{a}^{M*} }}{\partial \gamma } > 0$, otherwise, $\frac{{\partial p_{a}^{M*} }}{\partial \gamma } < 0$, where $W = \beta^{2} (v + \lambda N)^{2} - v^{2} (1 - k)(\beta^{2} + k^{2} v)$.

• (ii) The first-order conditions of Eq. (25) with respect to $N$ and $\lambda$ are $\frac{{\partial p_{u}^{M * } }}{\partial N} = \frac{{\beta \lambda_{u} (1 - k)(\beta + \gamma )}}{{4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k}}$ and $\frac{{\partial p_{u}^{M*} }}{\partial \lambda } = \frac{\beta N(1 - k)(\beta + \gamma )}{{4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k}}$. Obviously, $\frac{{\partial p_{u}^{M*} }}{\partial N} > 0$, $\frac{{\partial p_{u}^{M*} }}{\partial \lambda } > 0$.

The first-order condition of Eq. (25) with respect to γ is $\frac{{\partial p_{u}^{M*} }}{\partial \gamma } = \frac{(1 - k)(2\beta v + \lambda \beta N)}{{4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k}} + \frac{{(1 - k)(2\beta k - 4\beta + 2\gamma k)(2kv^{2} - 2k^{2} v^{2} + 2\beta \gamma v + \lambda \beta^{2} N + \lambda \beta \gamma N)}}{{\left[ {4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k} \right]^{2} }}.$

when $\gamma < \gamma_{1} = \frac{{2\sqrt {k(\beta^{2} + k^{2} v - kv)W} - 2k^{2} v^{2} (1 - k) - \lambda k\beta^{2} N}}{\beta k(2v + \lambda N)}$, we know $\frac{{\partial p_{u}^{M*} }}{\partial \gamma } < 0$, otherwise, $\frac{{\partial p_{u}^{M*} }}{\partial \gamma } > 0$.

• (iii) The first-order conditions of Eq. (26) with respect to $N$ and $\lambda$ are

$$ \begin{aligned} & \frac{{\partial p_{s}^{M*} }}{\partial N} = - \frac{{\lambda_{u} c_{s} kv\left[ {4kv(1 - k) - \beta \gamma k - \gamma^{2} k + 2\beta \gamma } \right]\left[ {4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k} \right]}}{{\alpha \left[ {4kv(1 - k)(kv + \lambda N) - (\beta + \gamma )(\beta kv + \lambda \beta N + \lambda \gamma N) + 2\beta \gamma \lambda N(1 + k) - \gamma^{2} kv + 3\beta \gamma kv} \right]{\kern 1pt}^{2} }}, \\ & \frac{{\partial p_{s}^{M*} }}{\partial \lambda } = - \frac{{Nc_{s} kv\left[ {4kv(1 - k) + 2\beta \gamma - \beta^{2} k - \gamma^{2} k} \right]\left[ {4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k} \right]}}{{\alpha \left[ {4kv(1 - k)(kv + \lambda N) - (\beta + \gamma )(\beta kv + \lambda \beta N + \lambda \gamma N) + 2\beta \gamma \lambda N(1 + k) - \gamma^{2} kv + 3\beta \gamma kv} \right]{\kern 1pt}^{2} }} \\ \end{aligned}. $$

According to Corollary 3, we can obtain $4kv(1 - k) - \beta \gamma k - \gamma^{2} k + 2\beta \gamma > 0$. According to Lemma 2, we can obtain $4kv(1 - k) + 4\beta \gamma - (\beta + \gamma )^{2} k < 0$. Obviously, $\frac{{\partial p_{s}^{M*} }}{\partial N} < 0$ and $\frac{{\partial p_{s}^{M*} }}{\partial \lambda } < 0$.

Therefore, Corollary 4 holds.

Proof of Proposition 1

By Eqs. (7) and (24), we have $p_{a}^{A*} - p_{a}^{M*} = \frac{\beta (v + \beta \gamma )}{2v + \beta \gamma } - \frac{{(\beta - \gamma )kv\left[{kv(1 - k) + \beta \gamma } \right] + 2\lambda_{u} kv\beta N(1 - k) - \lambda k\beta \gamma N(\beta + \gamma ) - 2\beta^{2} \lambda \gamma N}}{{(kv + \lambda N)\left[{\beta \gamma + 2kv(1 - k)} \right] + (\beta \gamma + 2kv)(1 - k)\lambda N}}$.

When $\gamma < \gamma_{2} = \frac{{\beta^{2} k(v - kv + k^{2} v - \lambda N) + 2\lambda \beta^{2} N(1 + \beta k^{2} - k - 2k^{2} v^{2} (1 - k)}}{{\beta k(kv - k^{2} v + v + \lambda N)}}$, we know $p_{a}^{A*} < p_{a}^{M*}$, otherwise, $p_{a}^{A*} > p_{a}^{M*}$.

Therefore, Proposition 1 holds.

The proof process of Propositions 2–3 is similar to that of Proposition 1, which is not discussed here.