Codimension two bifurcations of discrete Bonhoeffer–van der Pol oscillator model

Abstract

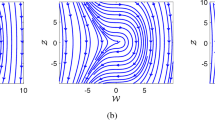
The non-degeneracy is one of the conditions to check for bifurcation analysis. Therefore, we need to compute the critical normal form coefficients to verify the non-degeneracy of the listed bifurcations. Using the critical normal form coefficients method to examine the bifurcation analysis makes it avoid calculating the central manifold and converting the linear part of the map into Jordan form. This is one of the most effective methods in the bifurcation analysis that has not received much attention so far. So in this article, we turn our attention to this method. In this study, the dynamic behaviors of the discrete Bonhoeffer–van der Pol (BVP) model are discussed. It is shown that the BVP model undergoes codimension one (codim-1) bifurcations such as pitchfork, fold, flip (period doubling) and Neimark–Sacker. Besides, codimension two (codim-2) bifurcations including resonance 1:2, 1:3, 1:4 and Chenciner have been achieved. For each bifurcation, normal form coefficients along with its scenario are investigated thoroughly. Bifurcation curves of the fixed points are drawn with the aid of numerical continuation techniques. Besides, a numerical continuation not only confirms our analytical results but also reveals richer dynamics of the model especially in the higher iteration.