Skip to main content
SpringerLink
Log in

Computational technique for heat and advection–diffusion equations

  • Application of soft computing
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

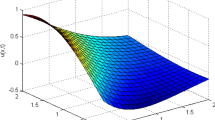
In the literature, several techniques are implemented to obtain the approximate solution of heat and advection–diffusion equations. However, each method involves certain drawbacks such as high arithmetic computations, lower accuracy in terms of error, and difficult for computer programming. In the present work, the octic B-spline collocation approach is implemented to incorporate the drawback of the other numerical studies in the literature with with high accuracy in terms of error and MATLAB programming is executed to compute the tedious calculation in an easy way toward the improvement of the approximate solution of heat and advection–diffusion equation. The time derivative is discretized by forward difference technique and the Crank–Nicolson scheme is applied for the remaining terms of the advection–diffusion equation. The stability of the scheme is examined and found that the scheme is unconditionally stable. To test the accuracy and efficiency of the scheme, four test problems are computed. A better approximate solution is obtained as compared to existing methods and a good agreement on analytical solutions by the proposed scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  • Askari M, Adibi H (2017) Numerical solution of advection-diffusion equation using meshless method of lines. Iran J Sci Technol Trans A: Sci 41:457–464

    MathSciNet  MATH  Google Scholar 

  • Bahar E, Gürarslan G (2017) Numerical solution of advection-diffusion equation using operator splitting method. Int J Eng Appl Sci 9:76–88

    Google Scholar 

  • Chawla MM, Al-Zanaidi MA, Al-Aslab MG (2000) Extended one-step time-integration schemes for convection-diffusion equations. Comput Math Appl 39:71–84

    MathSciNet  MATH  Google Scholar 

  • Cunha CLN, Carrer JAM, Oliveira MF, Costa VL (2016) A study concerning the solution of advection–diffusion problems by the Boundary Element Method. Eng Anal Boundary Elem 65:79–94

    MathSciNet  MATH  Google Scholar 

  • Dash P, Jena SR (2015) Mixed quadrature over sphere. Glob J Pure Appl Math 11(1):415–425

    Google Scholar 

  • Dehghan M (2004a) Numerical solution of the three-dimensional advection–diffusion equation. Appl Math Comput 150:5–19

    MathSciNet  MATH  Google Scholar 

  • Dehghan M (2004b) Weighted finite difference techniques for the one-dimensional advection–diffusion equation. Appl Math Comput 147:307–319

    MathSciNet  MATH  Google Scholar 

  • Dehghan M, Shirzadi M (2015) Meshless simulation of stochastic advection–diffusion equations based on radial basis functions. Eng Anal Boundary Elem 53:18–26

    MathSciNet  MATH  Google Scholar 

  • Demir DD, Bildik N (2012) The numerical solution of heat problem using cubic B-splines. Appl Math 2:131–135

    Google Scholar 

  • El-Baghdady GI, El-Azab MS (2015) Numerical solution of one-dimensional advection–diffusion equation with variable coefficients via legendre–gauss–lobatto time-space pseudo–spectral method. Electron J Math Anal Appl 3:1–14

    MathSciNet  MATH  Google Scholar 

  • Gebremedhin GS, Jena SR (2019) Approximate solution of ordinary differential equation via hybrid block approach. Int J Emerg Technol 10:210–211

    Google Scholar 

  • Gebremedhin GS, Jena SR (2020) Approximate of solution of a fourth order ordinary differential equations via tenth step block method. Int J Comput Sci Math 11:253–262

    MathSciNet  MATH  Google Scholar 

  • Goh J, Abd Majid A, Md Ismail AI (2012) Cubic B-spline collocation method for one-dimensional heat and advection-diffusion equations. J Appl Math, pp s1–8

  • Hasheminezhad A, Hadadi F, Shirmohammadi H (2021) Investigation and prioritization of risk factors in the collision of two passenger trains based on fuzzy COPRAS and fuzzy DEMATEL methods, Soft Comput

  • Hu W, Deng Z (2020) Interaction effects of DNA, RNA-polymerase, and cellular fluid on the local dynamic behaviors of DNA. Appl Math Mech 41:623–636

    MathSciNet  Google Scholar 

  • Hu W, Wang Z, Zhao Y, Deng Z (2020a) Symmetry breaking of infinite-dimensional dynamic system. Appl Math Lett 103:106207

    MathSciNet  MATH  Google Scholar 

  • Hu W, Yu L, Deng Z (2020b) Minimum control energy of spatial beam with assumed attitude adjustment target. Acta Mech Solida Sin 33:51–60

    Google Scholar 

  • Hu W, Zhang C, Deng Z (2020c) Vibration and elastic wave propagation in spatial flexible damping panel attached to four special springs. Commun Nonlinear Sci Numer Simul 84:105199

    MathSciNet  MATH  Google Scholar 

  • Isenberg J, Gutfinger C (1973) Heat transfer to a draining film. Int J Heat Mass Transf 16:505–512

    MATH  Google Scholar 

  • Jena SR, Dash P (2015a) Numerical treatment of analytic functions via mixed quadrature rule. Res J Appl Sci Eng Technol 10(4):391–392

    Google Scholar 

  • Jena SR, Dash P (2015b) An efficient quadrature rule for approximate solution of non linear integral equation of Hammerstein type. Int J Appl Eng Res 10(3):5831–5840

    Google Scholar 

  • Jena SR, Gebremedhin GS (2020) Approximate solution of a fifth order ordinary differential equation with block method. Int J Comput Sci Math 12:413–426

    MathSciNet  Google Scholar 

  • Jena SR, Gebremedhin GS (2021) Decatic B-spline collocation scheme for approximate solution of Burgers’ equation. Numer Methods Part Differ Equ. https://doi.org/10.1002/num.22747

    Article  Google Scholar 

  • Jena SR, Mishra SC (2015) Mixed quadrature for analytic functions. Glob J Pure Appl Math 1:281–285

    Google Scholar 

  • Jena SR, Nayak D (2020) Approximate instantaneous current in RLC circuit. Bull Electric Eng Inf 9(2):803–809

    Google Scholar 

  • Jena SR, Singh A (2015) A reliable treatment of analytic functions. Int J Appl Eng Res 10(5):11691–11695

    Google Scholar 

  • Jena SR, Meher K, Paul A (2016) Approximation of analytic functions in adaptive environment. Beni-Suef Univ J Basic Appl Sci 5:306–309

    Google Scholar 

  • Jena SR, Nayak D, Acharya MM (2017) Application of mixed quadrature rule on electromagnetic field problems. Comput Math Model 28(2):267–277

    MathSciNet  Google Scholar 

  • Jena SR, Mohanty M, Mishra SK (2018) Ninth step block method for numerical solution of fourth order ordinary differential equation. Adv Model Anal A 55(2):45–56

    Google Scholar 

  • Jena SR, Senapati A, Gebremedhin GS (2020a) Numerical study of solitions in BFRK scheme. Int J Mech Control 21(2):163–175

    Google Scholar 

  • Jena SR, Senapati A, Gebremedhin GS (2020b) Approximate solution of MRLW equation in B-spline environment. Math Sci 14(3):345–357

    MathSciNet  MATH  Google Scholar 

  • Jena SR, Nayak D, Paul AK, Mishra SC (2020c) Mixed anti-Newtonian-Gaussian rule for real definite integrals. Adv Math Sci J 9(11):1081–1090

    Google Scholar 

  • Korkmaz A, Dağ I (2016) Quartic and quintic B-spline methods for advection–diffusion equation. Appl Math Comput 274:208–219

    MathSciNet  MATH  Google Scholar 

  • Mittal RC, Jain RK (2012a) Numerical solution of convection-diffusion equation using cubic B-splines collocation methods with Neumann’s boundary conditions. Int J Appl Math Comput 4:115–127

    Google Scholar 

  • Mittal RC, Jain RK (2012b) Redefined cubic B-splines collocation method for solving convection–diffusion equations. Appl Math Model 36:5555–5573

    MathSciNet  MATH  Google Scholar 

  • Mohammadi R (2013) Exponential B-spline solution of convection-diffusion equations. Appl Math 04:933–944

    Google Scholar 

  • Mohanty M, Jena SR (2018) Differential transformation method (DTM) for approximate solution of ordinary differential equation (ODE). Adv Model Anal B 61:135–138

    Google Scholar 

  • Mohanty M, Jena SR, Mishra SK (2021) Approximate solution of fourth order differential equation. Adv Math Sci J 10(1):621–628

    Google Scholar 

  • Mohebbi A, Dehghan M (2010) High-order compact solution of the one-dimensional heat and advection–diffusion equations. Appl Math Model 34:3071–3084

    MathSciNet  MATH  Google Scholar 

  • Mojtabi A, Deville MO (2015) One-dimensional linear advection–diffusion equation: analytical and finite element solutions. Comput Fluids 107:189–195

    MathSciNet  MATH  Google Scholar 

  • Nazir T, Abbas M, Ismail AIM, Majid AA, Rashid A (2016) The numerical solution of advection–diffusion problems using new cubic trigonometric B-splines approach. Appl Math Model 40:4586–4611

    MathSciNet  MATH  Google Scholar 

  • Parlange JY (1980) Water transport in soils. Annu Rev Fluid Mech 12:77–102

    MATH  Google Scholar 

  • Sadeghi J, Hasheminezhad A, Essmayil-Kaboli M (2015) Investigation of the influences of track superstructure parameters on ballasted railway track design. Civ Eng Infrastruct Js 48:157–174

    Google Scholar 

  • Sanjaya F, Mungkasi S (2017) A simple but accurate explicit finite difference method for the advection-diffusion equation. J Phys: Conf Ser 909:1–5

    Google Scholar 

  • Sari M, Gürarslan G, Zeytinoğlu A (2010) High-order finite difference schemes for solving the advection-diffusion equation. Math Comput Appl 15:449–460

    MathSciNet  MATH  Google Scholar 

  • Singh H, Kumar D, Pandey RK (2020) An efficient computational method for the time-space fractional Klein-Gordon equation. Front Phys 8:1–7

    Google Scholar 

  • Zerroukat M, Djidjeli K, Charafi A (2000) Explicit and implicit meshless methods for linear advection diffusion-type partial diff erential equations. Int J Numer Meth Eng 48:19–35

    MathSciNet  MATH  Google Scholar 

  • Zhao J, Chen Z, Mehrmashhadi J, Bobaru F (2018) Construction of a peridynamic model for transient advection-diffusion problems. Int J Heat Mass Transf 126:1253–1266

    Google Scholar 

  • Zheng X, Wei Z (2015) Discontinuous legendre wavelet galerkin method for one-dimensional advection-diffusion equation. Appl Math 6:1581–1591

    Google Scholar 

  • Zlatev Z, Berkowicz R, Prahm LP (1984) Implementation of a variable stepsize variable formula method in the time-integration part of a code for treatment of long-range transport of air pollutants. J Comput Phys 55:278–301

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, School of Applied Sciences, KIIT Deemed To Be University, Bhubaneswar, Odisha, 751024, India

    Saumya Ranjan Jena & Guesh Simretab Gebremedhin

Authors
  1. Saumya Ranjan Jena
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guesh Simretab Gebremedhin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Saumya Ranjan Jena.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jena, S.R., Gebremedhin, G.S. Computational technique for heat and advection–diffusion equations. Soft Comput 25, 11139–11150 (2021). https://doi.org/10.1007/s00500-021-05859-2

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-021-05859-2

Keywords

Search

Navigation