Skip to main content
Springer Nature Link
Log in

Performance enhancement of meta-heuristics through random mutation and simulated annealing-based selection for concurrent topology and sizing optimization of truss structures

  • Optimization
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

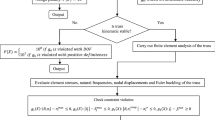
The present investigation includes the performance enhancement concept of discrete meta-heuristics (MHs) for truss design with concurrent size and topology optimization. The five basic MHs, viz. teaching–learning-based optimization (TLBO), whale optimization algorithm (WOA), dragonfly algorithm (DA), heat transfer search (HTS), and ant lion optimization (ALO) algorithm, are investigated. Often these MHs found incompetent in answering complex problems like concurrent topology and sizing optimization of truss structures due to their poor convergence rate, local optima trap, and higher computation time. Also, the balance between diversification and intensification is very significant for MHs efficiency. A mutation is a strong strategy for balancing the diversification and intensification of MHs and can assist in guiding the population towards the global optimum. Moreover, population diversity can be improved by incorporating the selection of simulated annealing that can reduce the chances of local optima tarp. Therefore, an effective search technique based on a random mutation search along with simulated annealing-based selection is developed. Here, five modified MHs, i.e. the modified DA (MDA), modified ALO (MALO), modified WOA (MWOA), modified HTS (MHTS), and modified TLBO (MTLBO) algorithms, using random mutation search phase and SA-based selection are proposed. The developed techniques are implemented on three standard test problems where dynamic and static constraints and multiple load cases are imposed. The comparative performance of the proposed algorithms and their original algorithms is carried out. An empirical evaluation was done using Friedman rank, and the respective algorithms ranks are assigned. The findings reveal that the new technique results in significant performance enhancement of the various MHs by synchronizing the diversification and intensification of search.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

MATLAB codes for all algorithms and design problems used in this study are available in https://drive.google.com/file/d/189RcD60j-wEx-43OK0D-t9KZGFAegRD4.

References

  • Arora S, Singh S (2019) Butterfly optimization algorithm: a novel approach for global optimization. Soft Comput 23(3):715–734

    Article  Google Scholar 

  • Asadpoure A, Tootkaboni M, Guest JK (2011) Robust topology optimization of structures with uncertainties in stiffness–Application to truss structures. Comput Struct 89(11–12):1131–1141

    Article  Google Scholar 

  • Bureerat S, Pholdee N (2016) Optimal truss sizing using an adaptive differential evolution algorithm. J Comput Civ Eng 30(2):04015019

    Article  Google Scholar 

  • Črepinšek M, Liu SH, Mernik L (2012) A note on teaching–learning-based optimization algorithm. Inf Sci 212:79–93

    Article  Google Scholar 

  • De Falco I, Della Cioppa A, Tarantino E (2002) Mutation-based genetic algorithm: performance evaluation. Appl Soft Comput 1(4):285–299

    Article  Google Scholar 

  • Deb K, Gulati S (2001) Design of truss-structures for minimum weight using genetic algorithms. Finite Elem Anal Des 37(5):447–465

    Article  MATH  Google Scholar 

  • Degertekin SO (2012) Improved harmony search algorithms for sizing optimization of truss structures. Comput Struct 92:229–241

    Article  Google Scholar 

  • Derrac J, García S, Molina D, Herrera F (2011) A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput 1(1):3–18

    Article  Google Scholar 

  • Dorn W (1964) Automatic design of optimal structures. J De Mecanique 3:25–52

    Google Scholar 

  • Eskandar H, Sadollah A, Bahreininejad A, Hamdi M (2012) Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput Struct 110:151–166

    Article  Google Scholar 

  • Fang H, Zhu G, Stojanovic V, Nie R, He S, Luan X, Liu F (2021) Adaptive optimization algorithm for nonlinear Markov jump systems with partial unknown dynamics. Int J Robust Nonlinear Control 31(6):2126–2140

    Article  MathSciNet  Google Scholar 

  • Feng X, Liu Y, Yu H, Luo F (2019) Physarum-energy optimization algorithm. Soft Comput 23(3):871–888

    MATH  Google Scholar 

  • Ghasemi-Marzbali A (2020) A novel nature-inspired meta-heuristic algorithm for optimization: bear smell search algorithm. Soft Comput 24(17):13003–13035

    Article  Google Scholar 

  • Gholizadeh S, Barzegar A (2013) Shape optimization of structures for frequency constraints by sequential harmony search algorithm. Eng Optim 45(6):627–646

    Article  MathSciNet  Google Scholar 

  • Gholizadeh S, Milany A (2018) An improved fireworks algorithm for discrete sizing optimization of steel skeletal structures. Eng Optim 50(11):1829–1849

    Article  MathSciNet  Google Scholar 

  • Gomes HM (2011) Truss optimization with dynamic constraints using a particle swarm algorithm. Expert Syst Appl 38(1):957–968

    Article  Google Scholar 

  • Gonçalves MS, Lopez RH, Miguel LFF (2015) Search group algorithm: a new metaheuristic method for the optimization of truss structures. Comput Struct 153:165–184

    Article  Google Scholar 

  • Kaveh A, Kalatjari V (2003) Topology optimization of trusses using genetic algorithm, force method and graph theory. Int J Numer Meth Eng 58(5):771–791

    Article  MATH  Google Scholar 

  • Kaveh A, Zolghadr A (2013) Topology optimization of trusses considering static and dynamic constraints using the CSS. Appl Soft Comput 13(5):2727–2734

    Article  Google Scholar 

  • Kaveh A, Zolghadr A (2014) Democratic PSO for truss layout and size optimization with frequency constraints. Comput Struct 130:10–21

    Article  Google Scholar 

  • Kaveh A, Hassani B, Shojaee S, Tavakkoli SM (2008) Structural topology optimization using ant colony methodology. Eng Struct 30(9):2559–2565

    Article  Google Scholar 

  • Khalilpourazari S, Khalilpourazary S (2019) An efficient hybrid algorithm based on Water Cycle and Moth-Flame Optimization algorithms for solving numerical and constrained engineering optimization problems. Soft Comput 23(5):1699–1722

    Article  Google Scholar 

  • Kirkpatrick S, Gelatt CD, Vecchi MP (1983) Optimization by simulated annealing. Science 220(4598):671–680

    Article  MathSciNet  MATH  Google Scholar 

  • Kirsch U (1989) Optimal topologies of truss structures. Comput Methods Appl Mech Eng 72(1):15–28

    Article  MathSciNet  MATH  Google Scholar 

  • Kumar S, Tejani GG, Mirjalili S (2019) Modified symbiotic organisms search for structural optimization. Engineering with Computers 35(4):1269–1296

    Article  Google Scholar 

  • Kumar S, Tejani GG, Pholdee N, Bureerat S (2020) Improved metaheuristics through migration-based search and an acceptance probability for truss optimization. Asian Journal of Civil Engineering 21(7):1217–1237

    Article  Google Scholar 

  • Kumar S, Tejani GG, Pholdee N, Bureerat S (2021d) Multi-objective modified heat transfer search for truss optimization. Engineering with Computers 37(4):3439–3454

    Article  Google Scholar 

  • Kumar, S., Tejani, G. G., Pholdee, N., Bureerat, S., & Jangir, P. (2021a). Multi-objective teaching-learning-based optimization for structure optimization. Smart Science, 1–12.

  • Kumar, S., Jangir, P., Tejani, G. G., Premkumar, M., & Alhelou, H. H. (2021b). MOPGO: A New Physics-Based Multi-Objective Plasma Generation Optimizer for Solving Structural Optimization Problems. IEEE Access.

  • Kumar, S., Tejani, G. G., Pholdee, N., & Bureerat, S. (2021c). Multiobjecitve structural optimization using improved heat transfer search. Knowledge-Based Systems, 219, 106811.

  • Kumar, S., Tejani, G. G., Pholdee, N., Bureerat, S., & Mehta, P. (2021e). Hybrid Heat Transfer Search and Passing Vehicle Search optimizer for multi-objective structural optimization. Knowledge-Based Systems, 212, 106556.

  • Kumar, S., Tejani, G. G., Pholdee, N., & Bureerat, S. (2021f) Multi-Objective Passing Vehicle Search algorithm for structure optimization. Expert Systems with Applications, 169, 114511.

  • Lamberti L (2008) An efficient simulated annealing algorithm for design optimization of truss structures. Comput Struct 86(19–20):1936–1953

    Article  Google Scholar 

  • Li L, Liu F (2011) Group search optimization for applications in structural design, vol 9. Springer, Berlin, Germany

    MATH  Google Scholar 

  • Li Z, Zhang X, Qin J, He J (2020) A reformative teaching–learning-based optimization algorithm for solving numerical and engineering design optimization problems. Soft Comput 24(20):15889–15906

    Article  Google Scholar 

  • Lu YC, Jan JC, Hung SL, Hung GH (2013) Enhancing particle swarm optimization algorithm using two new strategies for optimizing design of truss structures. Eng Optim 45(10):1251–1271

    Article  Google Scholar 

  • Mirjalili S (2015) The ant lion algorithm. Adv Eng Softw 83:80–98

    Article  Google Scholar 

  • Mirjalili S (2016) Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput Appl 27(4):1053–1073

    Article  MathSciNet  Google Scholar 

  • Mirjalili S, Lewis A (2016) The whale optimization algorithm. Adv Eng Softw 95:51–67

    Article  Google Scholar 

  • Ohsaki M (1995) Genetic algorithm for topology optimization of trusses. Comput Struct 57(2):219–225

    Article  MathSciNet  MATH  Google Scholar 

  • Ozbasaran H, Yildirim ME (2020) Truss-sizing optimization attempts with CSA: a detailed evaluation. Soft Comput 24(22):16775–16801

    Article  Google Scholar 

  • Pandey A, Datta R, Bhattacharya B (2017) Topology optimization of compliant structures and mechanisms using constructive solid geometry for 2-d and 3-d applications. Soft Comput 21(5):1157–1179

    Article  MATH  Google Scholar 

  • Patel VK, Savsani VJ (2015) Heat transfer search (HTS): a novel optimization algorithm. Inf Sci 324:217–246

    Article  Google Scholar 

  • Pholdee N, Bureerat S (2014) Comparative performance of meta-heuristic algorithms for mass minimisation of trusses with dynamic constraints. Adv Eng Softw 75:1–13

    Article  Google Scholar 

  • Piotrowski AP (2013) Adaptive memetic differential evolution with global and local neighborhood-based mutation operators. Inf Sci 241:164–194

    Article  Google Scholar 

  • Rao RV, Savsani VJ, Vakharia DP (2011) Teaching–learning-based optimization: a novel method for constrained mechanical design optimization problems. Comput Aided Des 43(3):303–315

    Article  Google Scholar 

  • Savsani VJ, Tejani GG, Patel VK (2016) Truss topology optimization with static and dynamic constraints using modified subpopulation teaching-learning-based optimization. Eng Optim 48(11):1990–2006

    Article  MathSciNet  Google Scholar 

  • Sonmez M (2011) Artifcial Bee Colony algorithm for optimization of truss structures. Appl Soft Comput 11(2):2406–2418

    Article  Google Scholar 

  • Tanabe, R., & Fukunaga, A. S. (2014, July). Improving the search performance of SHADE using linear population size reduction. In 2014 IEEE congress on evolutionary computation (CEC) (pp. 1658–1665). IEEE.

  • Tao H, Li J, Chen Y, Stojanovic V, Yang H (2020) Robust point-to-point iterative learning control with trial-varying initial conditions. IET Control Theory Appl 14(19):3344–3350

    Article  MathSciNet  Google Scholar 

  • Tejani GG, Savsani VJ, Patel VK (2016) Modified sub-population teaching-learning-based optimization for design of truss structures with natural frequency constraints. Mech Based Des Struct Mach 44(4):495–513

    Article  Google Scholar 

  • Tejani G, Savsani V, Patel V (2017) Modified sub-population based heat transfer search algorithm for structural optimization. International Journal of Applied Metaheuristic Computing (IJAMC) 8(3):1–23

    Article  Google Scholar 

  • Tejani GG, Savsani VJ, Bureerat S, Patel VK (2018) Topology and size optimization of trusses with static and dynamic bounds by modified symbiotic organisms search. J Comput Civ Eng 32(2):04017085

    Article  Google Scholar 

  • Tejani GG, Savsani VJ, Patel VK, Mirjalili S (2019) An improved heat transfer search algorithm for unconstrained optimization problems. Journal of Computational Design and Engineering 6(1):13–32

    Article  Google Scholar 

  • Tejani GG, Kumar S, Gandomi AH (2021) Multi-objective heat transfer search algorithm for truss optimization. Engineering with Computers 37(1):641–662

    Article  Google Scholar 

  • Teng ZJ, Lv JL, Guo LW (2019) An improved hybrid grey wolf optimization algorithm. Soft Comput 23(15):6617–6631

    Article  Google Scholar 

  • Torabi S, Safi-Esfahani F (2019) A hybrid algorithm based on chicken swarm and improved raven roosting optimization. Soft Comput 23(20):10129–10171

    Article  Google Scholar 

  • Waghmare G (2013) Comments on “A note on teaching–learning-based optimization algorithm.” Inf Sci 229:159–169

    Article  Google Scholar 

  • Wansasueb K, Bureerat S, Kumar S (2021) Ensemble of four metaheuristic using a weighted sum technique for aircraft wing design. Engineering and Applied Science Research 48(4):385–396

    Google Scholar 

  • Wei T, Li X, Stojanovic V (2021) Input-to-state stability of impulsive reaction–diffusion neural networks with infinite distributed delays. Nonlinear Dyn 103(2):1733–1755

    Article  Google Scholar 

  • Winyangkul S, Wansaseub K, Sleesongsom S, Panagant N, Kumar S, Bureerat S, Pholdee N (2021) Ground Structures-Based Topology Optimization of a Morphing Wing Using a Metaheuristic Algorithm. Metals 11(8):1311

    Article  Google Scholar 

  • Wolpert DH, Macready WG (1997) No free lunch theorems for optimization. IEEE Trans Evol Comput 1(1):67–82

    Article  Google Scholar 

  • Xu B, Jiang J, Tong W, Wu K (2003) Topology group concept for truss topology optimization with frequency constraints. J Sound Vib 261(5):911–925

    Article  Google Scholar 

  • Yi W, Zhou Y, Gao L, Li X, Mou J (2016) An improved adaptive differential evolution algorithm for continuous optimization. Expert Syst Appl 44:1–12

    Article  Google Scholar 

  • Zaeimi M, Ghoddosian A (2020) Color harmony algorithm: an art-inspired metaheuristic for mathematical function optimization. Soft Comput 24(16):12027–12066

    Article  Google Scholar 

Download references

Funding

This work was supported by the National Research Council of Thailand (NRCT).

Author information

Authors and Affiliations

  1. Australian Maritime College, College of Sciences and Engineering, University of Tasmania, Launceston, 7248, Australia

    Sumit Kumar

  2. Department of Mechanical Engineering, School of Technology, GSFC University, Vadodara, Gujarat, India

    Ghanshyam G. Tejani

  3. Sustainable and Infrastructure Research and Development Center, Department of Mechanical Engineering, Faculty of Engineering, Khon Kaen University, Khon Kaen, 40002, Thailand

    Nantiwat Pholdee & Sujin Bureerat

Authors
  1. Sumit Kumar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ghanshyam G. Tejani
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Nantiwat Pholdee
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Sujin Bureerat
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

SK contributed to conceptualization, methodology, writing–original draft, review and editing; GGT helped in conceptualization, methodology, software, formal analysis, data curation, writing–original draft, writing–review and editing, supervision, and project administration; NP performed conceptualization, methodology, software, formal analysis, data curation, writing–review and editing, supervision, and project administration; SB was involved in funding acquisition, conceptualization, methodology, software, formal analysis, data curation, writing–review and editing, supervision, and project administration

Corresponding author

Correspondence to Ghanshyam G. Tejani.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest.

Ethical approval

This work does not require ethical approval.

Informed consent

This work does not require informed consent.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, S., Tejani, G.G., Pholdee, N. et al. Performance enhancement of meta-heuristics through random mutation and simulated annealing-based selection for concurrent topology and sizing optimization of truss structures. Soft Comput 26, 5661–5683 (2022). https://doi.org/10.1007/s00500-022-06930-2

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-022-06930-2

Keywords