Swing-up control of an inverted pendulum cart system using the approach of Hedge-algebras theory

Abstract

The hedge-algebras (HA) theory has been effectively applied in different fields such as fuzzy database, logic programming, classification and regression, data mining, linguistic database summarization, and process control. This work presents a simple approach to design an HA-based controller in stabilizing a nonlinear and underactuated system, an inverted pendulum-cart model, including four input state variables and one output control variable. The HA-based controller is divided into four intermediate controllers with one input state and one output control variable. The combination method of the above intermediate controllers to achieve values of the global control variable in control loops is proposed following the influence level of state variables on the stable state of the system and the principle of HA-Inference step. The proposed approach is appropriate for controlling underactuated systems. Simulation results have indicated that the HA-based controller has high performance, adaptation, stability, and robustness. Moreover, the proposed method significantly reduces the computational time of the controller when compared to a classical Sugeno-type fuzzy controller.

Appendices

Appendix 1

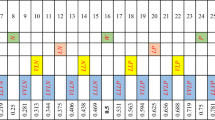
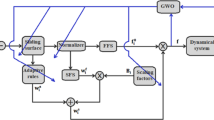
This section presents the parameters of the Sugeno-type fuzzy controller (FC). The algorithm diagram of FC is similar to that of HAC, as shown in Fig. 2, where.

• The fuzzification step of each state variable using triangular membership functions is represented in Fig. 

  Fig. 16

  

  Fuzzification step of each state variable

  16. Linguistic values L, Z, and R of each control variable are assigned by constants 0.25, 0.5, and 0.75, respectively.

• The rule base of FC is similar to that of HAC, as arranged in Table 3, where the linguistic value W is replaced by Z.

• Other parameters of the controller are given as follows:

  

• The inference step of FC is expressed by the relation shown in Fig. 17.

  Fig. 17

  

  The inference step of FC

• The defuzzification of FC iss the weighted average of all rule outputs.

Appendix 2

Equation (9) is rewritten in the state space as follows:

$$ {\dot{\mathbf{x}}} = {\mathbf{Ax}} + {\mathbf{Bu}} $$

(17)

The objective function with the minimum energy is chosen as:

$$ J({\mathbf{x}},{\mathbf{u}}) = \int\limits_{0}^{\infty } {({\mathbf{x}}^{T} {\mathbf{Qx}} + {\mathbf{u}}^{T} {\mathbf{Ru}})dt \to \min } $$

(18)

In which

$$ \begin{aligned} {\mathbf{Q}} &= {\mathbf{Q}}^{T} , \, {\mathbf{x}}^{T} {\mathbf{Qx}} \ge {\mathbf{0}},\quad \forall {\mathbf{x}} \hfill \\ {\mathbf{R}} &= {\mathbf{R}}^{T} , \, {\mathbf{x}}^{T} {\mathbf{Rx}} > {\mathbf{0}},\quad \forall {\mathbf{x}} \ne 0 \hfill \\ \end{aligned} $$

(19)

The Riccati equation is given as follows:

$$ - \left( {{\mathbf{KB}}} \right){\mathbf{R}}^{{{\mathbf{ - 1}}}} \left( {{\mathbf{B}}^{{\mathbf{T}}} {\mathbf{K}}} \right){\mathbf{ + KA + A}}^{{\mathbf{T}}} {\mathbf{K = Q}} $$

(20)

By solving Eq. (20) to calculate K, the control rule is obtained as:

$$ {\mathbf{u}}\left( t \right) = - {\mathbf{R}}^{ - 1} {\mathbf{B}}^{{\mathbf{T}}} {\mathbf{Kx}}(t) $$

(21)