Abstract
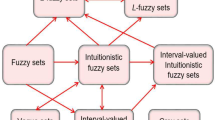
The picture fuzzy set (PFS) just appeared in 2014 and was introduced by Cuong, which is a generalization of intuitionistic fuzzy sets (Atanassov in Fuzzy Sets Syst 20(1):87–96, 1986) and fuzzy sets (Zadeh Inf Control 8(3):338–353, 1965). The picture fuzzy number (PFN) is an ordered value triple, including a membership degree, a neutral-membership degree, a non-membership degree, of a PFS. The PFN is a useful tool to study the problems that have uncertain information in real life. In this paper, the main aim is to develop basic foundations that can become tools for future research related to PFN and picture fuzzy calculus. We first establish a semi-linear space for PFNs by providing two new definitions of two basic operations, addition and scalar multiplication, such that the set of PFNs together with these two operations can form a semi-linear space. Moreover, we also provide some important properties and concepts such as metrics, order relations between two PFNs, geometric difference, multiplication of two PFNs. Next, we introduce picture fuzzy functions with a real domain that is also known as picture fuzzy functions with time-varying values, called geometric picture fuzzy function (GPFFs). In this framework, we give definitions about the limit of GPFFs and sequences of PFN. The important limit properties are also presented in detail. Finally, we prove that the metric semi-linear space of PFNs is complete, which is an important property in the classical mathematical analysis.



Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
All data generated or analyzed during this study are included in this article.
References
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96. https://doi.org/10.1016/S0165-0114(86)80034-3
Atanassov KT, Gargov G (1989) Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst 31(3):343–349. https://doi.org/10.1016/0165-0114(89)90205-4
Atanassov KT, Pasi G, Yager R (2005) Intuitionistic fuzzy interpretations of multi-criteria multi-person and multi-measurement tool decision making. Int J Syst Sci 36(14):859–868. https://doi.org/10.1080/00207720500382365
Chen TY (2011) A comparative analysis of score functions for multiple criteria decision making in intuitionistic fuzzy settings. Inf Sci 181(17):3652–3676. https://doi.org/10.1016/j.ins.2011.04.030
Cuong BC, Kreinovich V (2013) Picture fuzzy sets: a new concept for computational intelligence problems. In: Proceeding of 2013 third world congress on information and communication technologies (WICT 2013), pp 1–16. https://doi.org/10.1109/WICT.2013.7113099
Cuong BC (2014) Picture fuzzy sets. J Comput Sci Cybern 30(4):409–420. https://doi.org/10.15625/1813-9663/30/4/5032
De SK, Biswas R, Roy AR (2001) An application of intuitionistic fuzzy sets in medical diagnostic. Fuzzy Sets Syst 117(2):209–213. https://doi.org/10.1016/S0165-0114(98)00235-8
Diamond P, Kloeden P (2000) Metric topology of fuzzy numbers and fuzzy analysis. In: Dubois D, Prade H (eds) Fundamentals of fuzzy sets: the handbooks of fuzzy sets series. Springer, Boston. https://doi.org/10.1007/978-1-4615-4429-6-12
Dijkman JG, Van Haeringen H, De Lange SJ (1983) Fuzzy numbers. J Math Anal Appl 92(2):301–341. https://doi.org/10.1016/0022-247X(83)90253-6
Dubois D, Prade H (1982) Towards fuzzy differential calculus-part III: differentiation. Fuzzy Sets Syst 8(3):225–233. https://doi.org/10.1016/S0165-0114(82)80001-8
Dutta P, Ganju S (2017) Some aspects of picture fuzzy set. Trans A. Razmadze Math Inst 172(2):164–175. https://doi.org/10.1016/j.trmi.2017.10.006
Galanis GN (2009) Differentiability on semilinear spaces. Nonlinear Anal 71(10):4732–4738. https://doi.org/10.1016/j.na.2009.03.045
Khan S, Abdullah S, Abdullah L, Ashraf S (2019) Logarithmic aggregation operators of picture fuzzy numbers for multi-attribute decision making problems. Mathmatics 7(7):608. https://doi.org/10.3390/math7070608
Lei Q, Xu ZS (2017) Intuitionistic fuzzy calculus. Stud Fuzziness Soft Comput. https://doi.org/10.1007/978-3-319-54148-8
Moore RE, Kearfott RB, Cloud MJ (2009) Introduction to interval analysis. Soc Ind Appl Math SIAM. https://doi.org/10.1137/1.9780898717716
Phu ND, Hung NN, Quynh LTN (2021) Some new ordered semi-linear spaces of intuitionistic fuzzy processes and the pair of closely related states. In: Kahraman C., Cevik Onar S., Oztaysi B., Sari I., Cebi S., Tolga A. (eds) Intelligent and Fuzzy Techniques: Smart and Innovative Solutions. INFUS 2020. Advances in Intelligent Systems and Computing, vol.1197, Springer, Cham. https://doi.org/10.1007/978-3-030-51156-2-47
Phu ND, Hung NN (2018) The geometric lattice intuitionistic fuzzy functions and applications. J Intell Fuzzy Syst 35(3):3347–3358. https://doi.org/10.3233/JIFS-172027
Phu ND, Ahmadian A, Hung NN, Salahshour S, Senu N (2019) Narrow metric semi-linear space of intuitionistic fuzzy numbers: application to AIDS model. Int J Fuzzy Syst 21(6):1738–1754. https://doi.org/10.1007/s40815-019-00649-3
Phu ND, Hung NN, Ahmadian A, Salahshour S, Senu N (2021) Geometric picture fuzzy numbers and three-dimensional copulas with the non-linear programming approach. J Intell Fuzzy Syst 40(1):1–12. https://doi.org/10.3233/JIFS-182519
Rudin W (1976) Principles of mathematical analysis, 3rd edn. McGraw-Hill, New York
Shinoj TK, Sunil JJ (2012) Intuitionistic Fuzzy multisets and its application in medical diagnosis. World Acad Sci Eng Technol Int J Math Comput Phys Electr Comput Eng 6:1418–1421
Si A, Das S, Kar S (2019) An approach to rank picture fuzzy numbers for decision making problems. Decis Mak Appl Manag Eng 2(2):54–64. https://doi.org/10.31181/dmame1902049s
Son LH (2016) Generalized picture distance measure and applications to picture fuzzy clustering. Appl Soft Comput 46:284–295. https://doi.org/10.1016/j.asoc.2016.05.009
Takeuti G, Titani S (1984) Intuitionistic fuzzy logic and intuitionistic fuzzy set theory. J Symb Log 49(3):851–866. https://doi.org/10.2307/2274139
Thong NT, Son LH (2015) HIFCF: an effective hybrid model between picture fuzzy clustering and intuitionistic fuzzy recommender systems for medical diagnosis. Expert Syst Appl 42(7):3682–3701. https://doi.org/10.1016/j.eswa.2014.12.042
Wei G (2017) Picture fuzzy aggregation operators and their application to multiple attribute decision making. J Intell Fuzzy Syst 33(2):713–724. https://doi.org/10.3233/JIFS-161798
Worth RE (1970) Boundaries of semilinear spaces and semialgebras. Trans Am Math Soc 148:99–119
Xu ZS, Yager RR (2006) Some geometric aggregation operators based on intuitionistic fuzzy sets. Int J Gen Syst 35(4):417–433. https://doi.org/10.1080/03081070600574353
Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353
Acknowledgements
The authors are very grateful to the anonymous reviewer and associate editor for their insightful and constructive suggestions that have led to an improved version of this manuscript.
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Contributions
The authors declare that the study was realized in collaboration with equal responsibility. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Phu, N.D., Hung, N.N., Ahmadian, A. et al. Limit properties in the metric semi-linear space of picture fuzzy numbers. Soft Comput 26, 5481–5496 (2022). https://doi.org/10.1007/s00500-022-07017-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-022-07017-8