Skip to main content
Springer Nature Link
Log in

Pythagorean fuzzy inequality derived by operation, equality and aggregation operator

  • Foundations
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

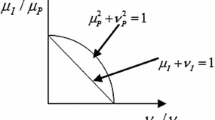
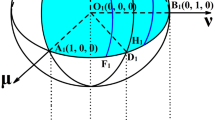
Pythagorean fuzzy set (PFS) is a meaningful generalization of intuitionistic fuzzy set, whose fascinating characteristic is that the sum of square of membership degree \(\mu \), non-membership degree \(\upsilon \) and hesitation degree \(\pi \) is equal to 1 with more flexible value space. Inequality on Pythagorean fuzzy set plays an important role in uncertainty theory. In this paper, we firstly derive some Pythagorean fuzzy inequalities based on some existing operations. Further, based on the existing operations, we develop three Pythagorean fuzzy aggregation operators, including Pythagorean fuzzy square (PFSq), Pythagorean fuzzy arithmetic and Pythagorean fuzzy geometric. Meanwhile, some inequalities on them are profoundly explored. Finally, we construct some Pythagorean fuzzy inequalities by equality \(\mu ^2+\upsilon ^2+\pi ^2=1\) in critical definition and prove them by some existing well-known inequalities, which will provide a new basis for Pythagorean fuzzy inequalities in operations and aggregation operators.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Akram M, Dudek W, Dar J (2019) Pythagorean Dombi fuzzy aggregation operators with application in multicriteria decision-making. Int J Intell Syst 34:3000–3019

    Article  Google Scholar 

  • Atanassov K (1986) Intuitionistic fuzzy sets. Fuzzy Set Syst 20:87–96

    Article  Google Scholar 

  • Bakula M, Pečarić J, Perić J (2012) On the converse Jensen inequality. Appl Math Comput 218:6566–6575

    MathSciNet  MATH  Google Scholar 

  • Bao S (2017) Proof of Vasc inequalities based on characteristics of convexity and concavity of functions. Stud Coll Math 20:29–30

    Google Scholar 

  • Bertolo J, Fernandez D (1984) A multidimensional version of the Carlson inequality. J Math Anal Appl 100:302–306

    Article  MathSciNet  Google Scholar 

  • Burk F (1987) The geometric, logarithmic, and arithmetic mean inequality. Am Math Mon 94:527–528

    Article  MathSciNet  Google Scholar 

  • Cooper C, Kennedy R (1989) Chebyshev’s inequality and natural density. Am Math Mon 96:118–124

    Article  MathSciNet  Google Scholar 

  • da Silva JD (1979) On the Schur inequality. Linear Multilinear A 7:343–357

    Article  MathSciNet  Google Scholar 

  • Draghici C (2005) A general rearrangement inequality. Proc Am Math Soc 133:735–743

    Article  MathSciNet  Google Scholar 

  • Du J, Liu S, Liu Y, Yi J (2022) A novel approach to three-way conflict analysis and resolution with Pythagorean fuzzy information. Inform Sci 584:65–88

    Article  Google Scholar 

  • Ejegwa P, Wen S, Feng Y, Zhang W, Tang N (2021) Novel Pythagorean fuzzy correlation measures via Pythagorean fuzzy deviation, variance and covariance with applications to pattern recognition and career placement. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/TFUZZ.2021.3063794

  • Huang C, Lin M, Xu Z (2020) Pythagorean fuzzy MULTIMOORA method based on distance measure and score function: its application in multicriteria decision making process. Knowl Inf Syst 62:4373–4406

    Article  Google Scholar 

  • Janani K, Veerakumari K, Vasanth K, Rakkiyappan R (2022) Complex Pythagorean fuzzy Einstein aggregation operators in selecting the best breed of Horsegram. Expert Syst Appl 187:115990

    Article  Google Scholar 

  • Lang G, Miao D, Fujita H (2020) Three-way group conflict analysis based on Pythagorean fuzzy set theory. IEEE Trans Fuzzy Syst 28:447–461

    Article  Google Scholar 

  • Lin M, Chen Y, Chen R (2021) Bibliometric analysis on Pythagorean fuzzy sets during 2013–2020. Int J Intell Comput Cybern 14:104–121

    Article  Google Scholar 

  • Maligranda L (2012) The AM-GM inequality is equivalent to the Bernoulli inequality. Math Intell 34:1–2

    Article  MathSciNet  Google Scholar 

  • Paris J, Vencovska A (2009) A generalization of Muirhead’s inequality. J Math Inequal 3:181–187

    Article  MathSciNet  Google Scholar 

  • Peng X (2019) Algorithm for Pythagorean fuzzy multi-criteria decision making based on WDBA with new score function. Fund Inform 165:99–137

    MathSciNet  MATH  Google Scholar 

  • Peng X, Yang Y (2015) Some results for Pythagorean fuzzy sets. Int J Intell Syst 30:1133–1160

    Article  Google Scholar 

  • Peng X, Zhang X, Luo Z (2020) Pythagorean fuzzy MCDM method based on CoCoSo and CRITIC with score function for 5G industry evaluation. Artif Intell Rev 53:3813–3847

    Article  Google Scholar 

  • Pratt R (2010) Proof without words: a tangent inequality. Math Mag 8:110

    Article  Google Scholar 

  • Tolsted E (1964) An elementary derivation of the Cauchy, Holder, and Minkowski inequalities from Young’s inequality. Math Mag 37:2–12

    Article  MathSciNet  Google Scholar 

  • Wang Q (2013) Some Nesbitt type inequalities with applications for the Zeta functions. J Math Inequal 7:523–527

    Article  MathSciNet  Google Scholar 

  • Wang L, Garg H (2021) Algorithm for multiple attribute decision-making with interactive Archimedean norm operations under Pythagorean fuzzy uncertainty. Int J Comput Intell Syst 14:503–527

    Article  Google Scholar 

  • Wang M, Chu Y, Qiu Y, Qiu S (2011) An optimal power mean inequality for the complete elliptic integrals. Appl Math Lett 24:887–890

    Article  MathSciNet  Google Scholar 

  • Yager R (2014) Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst 22:958–965

    Article  Google Scholar 

  • Yager R, Abbasov A (2013) Pythagorean membership grades, complex numbers, and decision making. Int J Intell Syst 28:436–452

    Article  Google Scholar 

  • Yang Z (2018) Abel’s identities and classical inequalities and their applications, 6th edn. HIT Press, Harbin

    Google Scholar 

  • Zhang Y (2014) Wei–Wei dual inequality and its applications, 2nd edn. USTC Press, Hefei

    Google Scholar 

  • Zhang X (2016) A novel approach based on similarity measure for pythagorean fuzzy multiple criteria group decision making. Int J Intell Syst 31:593–611

    Article  Google Scholar 

  • Zhang X, Xu Z (2014) Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst 29:1061–1078

    Article  Google Scholar 

  • Zhao B (2005) Half concave and half convex theorem, http://mathlinks.ro/community/h64933

  • Zhou Y, Zheng C, Goh M (2022) Statistics-based approach for large-scale group decision-making under incomplete Pythagorean fuzzy information with risk attitude. Knowl-Based Syst 235:107654

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China under Grants 62006155 and 62102261.

Author information

Authors and Affiliations

  1. College of Computer, National University of Defense Technology, Changsha, 410073, China

    Xindong Peng & Zhigang Luo

  2. School of Information Engineering, Shaoguan University, Shaoguan, 512005, China

    Xindong Peng

Authors
  1. Xindong Peng
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhigang Luo
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All authors contributed to the study conception and design. Material preparation was performed by Xindong Peng. The first draft of the manuscript was written by Xindong Peng and then polished by Zhigang Luo. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Xindong Peng.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Informed consent

Informed consent was obtained from all individual participants included in the study.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Peng, X., Luo, Z. Pythagorean fuzzy inequality derived by operation, equality and aggregation operator. Soft Comput 26, 5975–6018 (2022). https://doi.org/10.1007/s00500-022-07078-9

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-022-07078-9

Keywords