Skip to main content
Springer Nature Link
Log in

Dombi operations for linguistic T-spherical fuzzy number: an approach for selection of the best variety of maize

  • Fuzzy systems and their mathematics
  • Published:
Soft Computing Aims and scope Submit manuscript

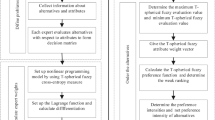
Abstract

The operations proposed by Dombi based on t-norn (TN) and t-corom (TCN) are generally known as Dombi operations, which offer versatility in the working behavior of parameters. Over the last decade, group decision-making has been a very active research field. Especially, the development of new operational rules, aggregation operators, and multi-attribute group decision-making techniques based on these rules and operators have recently piqued the interest of scientists. Acknowledging the importance of t-spherical fuzzy sets and linguistic variable in this paper, firstly, we define the notion of linguistic T-spherical fuzzy set (Lt-SFS) where membership degree, abstinence degree and non-membership degree are presented in the form of linguistic variables. Dombi operations, score function, accuracy function for linguistic T-spherical fuzzy numbers (Lt-SFNs) are defined and some prominent properties of Dombi operations are then investigated. Furthermore, two aggregations operators based on Dombi operations namely, linguistic t-spherical fuzzy Dombi weighted averaging operator and linguistic t-spherical fuzzy Dombi weighted geometric operator are also developed. At that point, these Dombi operators are used to establish an extension of the technique for order of preference by similarity to ideal solution (TOPSIS) method, and a multi-attribute group decision-making approach is proposed to solve decision-making problems which is the key innovation of this paper. Finally, we apply the proposed technique for the selection of the best variety of maize and a comparison analysis is provided to demonstrate its applicability and feasibility.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

The authors declare that data supporting the findings of this study are included into this manuscript.

References

  • Ali Z, Mahmood T (2020) Maclaurin symmetric mean operators and their applications in the environment of complex q-rung orthopair fuzzy sets. Comput Appl Math 39:1–27

    Article  MathSciNet  MATH  Google Scholar 

  • Arqub OA (2017) Adaptation of reproducing kernel algorithm for solving fuzzy Fredholm-Volterra integrodifferential equations. Neural Comput Appl 28:1591–1610

    Article  Google Scholar 

  • Arqub OA, Al-Smadi M, Momani S, Hayat T (2017) Application of reproducing kernel algorithm for solving second-order, two-point fuzzy boundary value problems. Soft Comput 21:7191–7206

    Article  MATH  Google Scholar 

  • Arqub OA, Singh J, Alhodaly (2021a) M Adaptation of kernel functions-based approach with Atangana–Baleanu–Caputo distributed order derivative for solutions of fuzzy fractional Volterra and Fredholm integrodifferential equations. Math Methods Appl Sci n/a: https://doi.org/10.1002/mma.7228

  • Arqub OA, Singh J, Maayah B, Alhodaly M (2021b) Reproducing kernel approach for numerical solutions of fuzzy fractional initial value problems under the Mittag–Leffler kernel differential operator. Math Methods Appl Sci n/a: https://doi.org/10.1002/mma.7305

  • Atanassov KT (1999a) Intuitionistic fuzzy sets. In: Intuitionistic fuzzy sets. Studies in Fuzziness and Soft Computing. Physica, Heidelberg pp 1–137. https://doi.org/10.1007/978-3-7908-1870-3_1

  • Atanassov KT (1999b) Interval valued intuitionistic fuzzy sets. In: Intuitionistic Fuzzy Sets. Studies in Fuzziness and Soft Computing, vol 35. Physica, Heidelberg. https://doi.org/10.1007/978-3-7908-1870-3_2

  • Aydemir SB, Gündüz SY (2020) Extension of multi-Moora method with some q-rung orthopair fuzzy Dombi prioritized weighted aggregation operators for multi-attribute decision making. Soft Comput 24:18545–18563

    Article  MATH  Google Scholar 

  • Chen T-Y, Tsao C-Y (2008) The interval-valued fuzzy TOPSIS method and experimental analysis. Fuzzy Sets Syst 159:1410–1428

    Article  MathSciNet  MATH  Google Scholar 

  • Chen J, Ye J (2017) Some single-valued neutrosophic Dombi weighted aggregation operators for multiple attribute decision-making. Symmetry (basel) 9:82

    Article  Google Scholar 

  • Chen Z, Liu P, Pei Z (2015) An approach to multiple attribute group decision making based on linguistic intuitionistic fuzzy numbers. Int J Comput Intell Syst 8:747–760

    Article  Google Scholar 

  • Chu T-C, Lin Y-C (2003) A fuzzy TOPSIS method for robot selection. Int J Adv Manuf Technol 21:284–290

    Article  Google Scholar 

  • Cuong BC, Kreinovich V (2013) Picture fuzzy sets-a new concept for computational intelligence problems. In: 2013 third world congress on information and communication technologies (WICT 2013). IEEE, pp 1–6

  • Dick S, Yager RR, Yazdanbakhsh O (2015) On Pythagorean and complex fuzzy set operations. IEEE Trans Fuzzy Syst 24:1009–1021

    Article  Google Scholar 

  • Dombi J (1982) A general class of fuzzy operators, the DeMorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst 8:149–163

    Article  MathSciNet  MATH  Google Scholar 

  • Dutta P, Ganju S (2018) Some aspects of picture fuzzy set. Trans A Razmadze Math Inst 172:164–175

    Article  MathSciNet  MATH  Google Scholar 

  • Garg H (2018) Linguistic Pythagorean fuzzy sets and its applications in multiattribute decision-making process. Int J Intell Syst 33:1234–1263

    Article  Google Scholar 

  • Garg H (2019) New logarithmic operational laws and their aggregation operators for Pythagorean fuzzy set and their applications. Int J Intell Syst 34:82–106

    Article  Google Scholar 

  • Garg H (2020) Linguistic interval-valued Pythagorean fuzzy sets and their application to multiple attribute group decision-making process. Cognit Comput 12:1313–1337

    Article  Google Scholar 

  • Garg H (2021) A new possibility degree measure for interval-valued q-rung orthopair fuzzy sets in decision-making. Int J Intell Syst 36:526–557

    Article  Google Scholar 

  • Garg H, Chen S-M (2020) Multiattribute group decision making based on neutrality aggregation operators of q-rung orthopair fuzzy sets. Inf Sci (ny) 517:427–447

    Article  MathSciNet  MATH  Google Scholar 

  • Garg H, Kaur G (2020) Extended TOPSIS method for multi-criteria group decision-making problems under cubic intuitionistic fuzzy environment. Sci Iran 27:396–410

    Google Scholar 

  • Garg H, Kumar K (2020) Group decision making approach based on possibility degree measure under linguistic interval-valued intuitionistic fuzzy set environment. J Ind Manag Optim 16:445

    Article  MathSciNet  MATH  Google Scholar 

  • Gomes LFAM, Lima MMPP (1991) TODIMI: basics and application to multicriteria ranking. Found Comput Decis Sci 16(3–4):1–16

  • Gomes L, Lima M (1992) From modeling individual preferences to multicriteria ranking of discrete alternatives: a look at prospect theory and the additive difference model. Found Comput Decis Sci 17:171–184

    MATH  Google Scholar 

  • Gurmani SH, Chen H, Bai Y (2021) The operational properties of linguistic interval valued q-Rung orthopair fuzzy information and its VIKOR model for multi-attribute group decision making. Intell Fuzzy Syst 41:7063–7079

    Article  Google Scholar 

  • Jahanshahloo GR, Lotfi FH, Izadikhah M (2006) Extension of the TOPSIS method for decision-making problems with fuzzy data. Appl Math Comput 181:1544–1551

    MATH  Google Scholar 

  • Jana C, Muhiuddin G, Pal M (2019) Some Dombi aggregation of Q-rung orthopair fuzzy numbers in multiple-attribute decision making. Int J Intell Syst 34:3220–3240

    Article  Google Scholar 

  • Jin H, Ashraf S, Abdullah S et al (2019) Linguistic spherical fuzzy aggregation operators and their applications in multi-attribute decision making problems. Mathematics 7:413

    Article  Google Scholar 

  • Khalil AM, Li S-G, Garg H et al (2019) New operations on interval-valued picture fuzzy set, interval-valued picture fuzzy soft set and their applications. IEEE Access 7:51236–51253

    Article  Google Scholar 

  • Khan AA, Ashraf S, Abdullah S et al (2019) Pythagorean fuzzy Dombi aggregation operators and their application in decision support system. Symmetry (basel) 11:383

    Article  MATH  Google Scholar 

  • Lai Y-J, Liu T-Y, Hwang C-L (1994) TOPSIS for MODM. Eur J Oper Res 76:486–500. https://doi.org/10.1016/0377-2217(94)90282-8

    Article  MATH  Google Scholar 

  • Lin M, Li X, Chen L (2020) Linguistic q-rung orthopair fuzzy sets and their interactional partitioned Heronian mean aggregation operators. Int J Intell Syst 35:217–249

    Article  Google Scholar 

  • Liu P, Liu J (2018) Some q-rung orthopai fuzzy Bonferroni mean operators and their application to multi-attribute group decision making. Int J Intell Syst 33:315–347

    Article  Google Scholar 

  • Liu P, Wang P (2018) Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int J Intell Syst 33:259–280

    Article  Google Scholar 

  • Liu P, Chen S-M, Wang P (2018) Multiple-attribute group decision-making based on q-rung orthopair fuzzy power maclaurin symmetric mean operators. IEEE Trans Syst Man, Cybern Syst 50:3741–3756

    Google Scholar 

  • Liu D, Luo Y, Liu Z (2020) The linguistic picture fuzzy set and its application in multi-criteria decision-making: an illustration to the TOPSIS and TODIM methods based on entropy weight. Symmetry (basel) 12:1170

    Article  Google Scholar 

  • Liu P, Liu J, Chen S-M (2017) Some intuitionistic fuzzy Dombi Bonferroni mean operators and their application to multi-attribute group decision making. J Oper Res Soc 69:1–24. https://doi.org/10.1057/s41274-017-0190-y

    Article  Google Scholar 

  • Mahmood T, Ullah K, Khan Q, Jan N (2019) An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput Appl 31:7041–7053

    Article  Google Scholar 

  • Mohanasundari M, Mohana K (2020) Quadripartitioned single valued neutrosophic Dombi weighted aggregation operators for multiple attribute decision making. Neutrosophic Sets Syst 32:9

    Google Scholar 

  • Molodtsov D (1999) Soft set theory—first results. Comput Math with Appl 37:19–31

    Article  MathSciNet  MATH  Google Scholar 

  • Opricovic´ S, (1998) VIKOR method. Multicriteria Optim Civ Eng Syst Univ Belgrade-Faculty Civ Eng Belgrade 2(1):142–175

    MathSciNet  Google Scholar 

  • Pang Q, Wang H, Xu Z (2016) Probabilistic linguistic term sets in multi-attribute group decision making. Inf Sci (ny) 369:128–143

    Article  Google Scholar 

  • Pawlak Z (1982) Rough sets. Int J Comput Inf Sci 11:341–356

    Article  MATH  Google Scholar 

  • Peng X (2019) New operations for interval-valued Pythagorean fuzzy set. Sci Iran Trans E Ind Eng 26:1049–1076

    Google Scholar 

  • Peng X, Selvachandran G (2019) Pythagorean fuzzy set: state of the art and future directions. Artif Intell Rev 52:1873–1927

    Article  Google Scholar 

  • Qiyas M, Abdullah S, Ashraf S, Abdullah L (2019) Linguistic picture fuzzy Dombi aggregation operators and their application in multiple attribute group decision making problem. Mathematics 7:764

    Article  Google Scholar 

  • Qiyas M, Khan MA, Khan S, Abdullah S (2020) Concept of Yager operators with the picture fuzzy set environment and its application to emergency program selection. Int J Intell Comput Cybern 13:455–483. https://doi.org/10.1108/IJICC-06-2020-0064

    Article  Google Scholar 

  • Rodriguez RM, Martinez L, Herrera F (2011) Hesitant fuzzy linguistic term sets for decision making. IEEE Trans Fuzzy Syst 20:109–119

    Article  Google Scholar 

  • Rouyendegh BD, Yildizbasi A, Üstünyer P (2020) Intuitionistic fuzzy TOPSIS method for green supplier selection problem. Soft Comput 24:2215–2228

    Article  Google Scholar 

  • Saaty TL (1977) A scaling method for priorities in hierarchical structures. J Math Psychol 15:234–281

    Article  MathSciNet  MATH  Google Scholar 

  • Sahu R, Dash SR, Das S (2021) Career selection of students using hybridized distance measure based on picture fuzzy set and rough set theory. Decis Mak Appl Manag Eng 4:104–126

    Article  Google Scholar 

  • Sajjad AKM, Sultan KA, Ali KI et al (2021) Linguistic interval-valued q-rung orthopair fuzzy TOPSIS method for decision making problem with incomplete weight J Intell Fuzzy Syst 40:4223–4235

    Google Scholar 

  • Son LH (2016) Generalized picture distance measure and applications to picture fuzzy clustering. Appl Soft Comput 46:284–295

    Article  Google Scholar 

  • Son LH, Van Viet P, Van Hai P (2017) Picture inference system: a new fuzzy inference system on picture fuzzy set. Appl Intell 46:652–669

    Article  Google Scholar 

  • Thao NX, Dinh NV (2015) Rough picture fuzzy set and picture fuzzy topologies. Sci Comput Cybern 31:245–254

    Google Scholar 

  • Torra V (2010) Hesitant fuzzy sets. Int J Intell Syst 25:529–539

    MATH  Google Scholar 

  • Ullah K, Mahmood T, Jan N (2018) Similarity measures for T-spherical fuzzy sets with applications in pattern recognition. Symmetry (basel) 10:193

    Article  MATH  Google Scholar 

  • Ullah K, Hassan N, Mahmood T et al (2019) Evaluation of investment policy based on multi-attribute decision-making using interval valued T-spherical fuzzy aggregation operators. Symmetry (basel) 11:357

    Article  Google Scholar 

  • Ullah K, Garg H, Mahmood T et al (2020) Correlation coefficients for T-spherical fuzzy sets and their applications in clustering and multi-attribute decision making. Soft Comput 24:1647–1659

    Article  MATH  Google Scholar 

  • Wang P, Wang J, Wei G, Wei C (2019) Similarity measures of q-rung orthopair fuzzy sets based on cosine function and their applications. Mathematics 7:340

    Article  Google Scholar 

  • Wei G, Gao H, Wei Y (2018) Some q-rung orthopair fuzzy Heronian mean operators in multiple attribute decision making. Int J Intell Syst 33:1426–1458

    Article  Google Scholar 

  • Wu M-Q, Chen T-Y, Fan J-P (2019) Divergence measure of T-spherical fuzzy sets and its applications in pattern recognition. IEEE Access 8:10208–10221

    Article  Google Scholar 

  • Yager RR (2016) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25:1222–1230

    Article  Google Scholar 

  • Yager RR, Abbasov AM (2013) Pythagorean membership grades, complex numbers, and decision making. Int J Intell Syst 28:436–452

    Article  Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inf. Control 8:338–353. https://doi.org/10.1016/S0019-9958(65)90241-X

    Article  MathSciNet  MATH  Google Scholar 

  • Zadeh LA (1975a) The concept of a linguistic variable and its application to approximate reasoning—II. Inf Sci (ny) 8:301–357

    Article  MathSciNet  MATH  Google Scholar 

  • Zadeh LA (1975b) The concept of a linguistic variable and its application to approximate reasoning-III. Inf Sci (ny) 9:43–80

    Article  MathSciNet  MATH  Google Scholar 

  • Zadeh LA (1975c) The concept of a linguistic variable and its application to approximate reasoning—I. Inf Sci (ny) 8:199–249

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are thankful to the anonymous reviewers for their valuable comments and constructive suggestions that have led to an improved version of this paper.

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 71871001, 71771001, 72001001); Natural Science Foundation for Distinguished Young Scholars of Anhui Province (No. 1908085J03); Research Funding Project of Academic and technical leaders and reserve candidates in Anhui Province (No.2018H179).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Anhui University, Hefei, 230601, Anhui, China

    Shahid Hussain Gurmani, Huayou Chen & Yuhang Bai

Authors
  1. Shahid Hussain Gurmani
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Huayou Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yuhang Bai
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Shahid Hussain Gurmani: Conceptualization, Formal analysis, Writing – original draft, Writing – review & editing, Methodology. Huayou Chen: Supervision, Investigation, Validation, Writing—review & editing. Yuhang Bai: Calculation, Software.

Corresponding author

Correspondence to Huayou Chen.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Ethical approval

This paper was approved by academic committee of School of Mathematical sciences, Anhui University.

Informed consent

All authors agreed to this submission.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gurmani, S.H., Chen, H. & Bai, Y. Dombi operations for linguistic T-spherical fuzzy number: an approach for selection of the best variety of maize. Soft Comput 26, 9083–9100 (2022). https://doi.org/10.1007/s00500-022-07307-1

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-022-07307-1

Keywords