Skip to main content

Advertisement

Springer Nature Link
Log in

Multiple attribute decision-making based on maclaurin symmetric mean operators on q-rung orthopair cubic fuzzy sets

  • Fuzzy systems and their mathematics
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

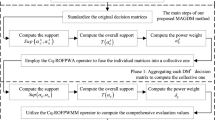
In this paper, the multiple attribute decision-making problems in which the attribute values take the form of q-rung orthopair cubic fuzzy sets (qRCOFSs) are investigated. Firstly, the definition of qROCFSs and some operational laws of qROCFSs are proposed. Then, a family of q-rung orthopair cubic fuzzy maclaurin symmetric mean aggregation operators are developed, such as the q-rung orthopair cubic fuzzy maclaurin symmetric mean (q-ROCFMSM) operator, the q-rung orthopair cubic fuzzy weighted maclaurin symmetric mean (q-ROCFWMSM) operator, the q-rung orthopair cubic fuzzy dual maclaurin symmetric mean (q-ROCFDMSM) operator, the q-rung orthopair cubic fuzzy weighted dual maclaurin symmetric mean (q-ROCFWDMSM) operator. And the properties and special cases of these proposed operators are studied. Furthermore, an approach based on the q-ROCFWMSM operator and the q-ROCFWDMSM operator is proposed for multiple attribute decision-making problems under q-rung orthopair cubic fuzzy environment. Finally, a numerical example and comparative analysis is given to illustrate the application of the proposed approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

Enquiries about data availability should be directed to the authors.

References

  • Aldo JVS, Luis P, Erwin MG, David LC, Delia VR (2021) Dimensional Analysis under Linguistic Pythagorean. Fuzzy Set Symmetry. 13(440):440

    Google Scholar 

  • Aliya F, Saleem A, Fazli A (2021a) Aggregation operators on cubic linguistic hesitant fuzzy numbers and their application in group decision-making. Granular Comput 6(2):1–18

    Google Scholar 

  • Aliya F, Naveed Y, Wathek C (2021) Maclaurin symmetric mean aggregation operators based on cubic Pythagorean linguistic fuzzy number. J Amb Intel Hum Comp 12(20):1925–1942

    Google Scholar 

  • Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96

    Article  MATH  Google Scholar 

  • Ayub S, Abdullah S, Ghani F, Qiyas M, Yaqub KM (2021) Cubic fuzzy heronian mean dombi aggregation operators and their application on multi attribute decision making problem soft computing a fusion of foundations. Methodol. Appl. 25(6):4175–4189

    Google Scholar 

  • Azim AB, Ali A, Ali S, Fahmi A, Siddiqa A (2021) A new approach of cubic interval-valued intuitionistic fuzzy subsemigroup and ideals. Granular Comput 6(2):1–18

    Article  Google Scholar 

  • Detemple D, Robertson J (1979) On generalized symmetric means of two variables Univ. Beograd Publ Elektrotehn FakSer Mat Fiz. 236–238

  • Feng X, Shang XP, Xu Y, Wang J (2020) A method to multi-attribute decision-making based on interval-valued q-rung dual hesitant linguistic Maclaurin symmetric mean operators. Complex Intell Syst. 693:447–468

    Article  Google Scholar 

  • Garg H, Ali Z, Mahmood T (2021) Algorithms for complex interval-valued q-rung orthopair fuzzy sets in decision making based on aggregation operators. AHP, and TOPSIS Expert Syst 38(1):1–36

    Google Scholar 

  • Gülçin B, Fethullah G, Deniz U (2021) A novel Pythagorean fuzzy set integrated Choquet integral approach for vertical farming technology assessment. Comput Ind Eng 158:107384

    Article  Google Scholar 

  • Harish G, Rishu A (2020) Maclaurin symmetric mean aggregation operators based on t-norm operations for the dual hesitant fuzzy soft set. J Amb Intel Hum Comp 11(1):375–410

    Article  Google Scholar 

  • Harish G, Zeeshan A, Mahmood T (2021) Generalized dice similarity measures for complex q-Rung Orthopair fuzzy sets and its application. Complex Intell Syst. 7(2):667–686

    Article  Google Scholar 

  • He X, Li Y, Qin K, Meng D (2019) Distance measures on intuitionistic fuzzy sets based on intuitionistic fuzzy dissimilarity functions. Soft Comput. 24(1):523–541

    Article  MATH  Google Scholar 

  • Jin CX, Ran Y, Zhang GB (2021) Interval-valued q-rung orthopair fuzzy FMEA application to improve risk evaluation process of tool changing manipulator Appl. Soft Comput 14:107192

    Article  Google Scholar 

  • Jun YB, Kim CS, Yang KO (2012) Cubic Set. Ann Fuzzy Math Inf 4(1):83–98

    MathSciNet  Google Scholar 

  • Lang GM, Miao DQ, Fujita H (2020) Three-way group conflict analysis based on pythagorean fuzzy set theory. IEEE Trans Fuzzy Syst 28(3):447–461

    Article  Google Scholar 

  • Liu PD, Yang HY (2020) Three-way decisions with intuitionistic uncertain linguistic decision-theoretic rough sets based on generalized maclaurin symmetric mean operators. Int Fuzzy Syst 22(2):653–667

    Article  Google Scholar 

  • Liu PD, Chen SYM, Wang P (2020a) Multiple-attribute group decision-making based on q-rung orthopair fuzzy power maclaurin symmetric mean operators. IEEE T Syst Man CY-S 50(10):3741–3756

    Google Scholar 

  • Liu PD, Chen SYM, Wang YM (2020b) Multiattribute group decision making based on intuitionistic fuzzy partitioned Maclaurin symmetric mean operators. Inf Sci 512:830–854

    Article  MathSciNet  MATH  Google Scholar 

  • Liu Y, Wei GW, Abdullah S, Liu J, Xu L, Liu HB (2021) Banzhaf–Choquet-copula-based aggregation operators for managing q-rung orthopair fuzzy information. Soft Comput. 25(10):6891–6914

    Article  Google Scholar 

  • Liu PD, Pan Q, Xu HX (2021) Multi-attributive border approximation area comparison (MABAC) method based on normal q-rung orthopair fuzzy environment. J Intell Fuzzy Syst. 40(5):1–27

    Google Scholar 

  • Liu HB, Liu Y, Xu L, Abdullah S (2021c) Multi-attribute group decision-making for online education live platform selection based on linguistic intuitionistic cubic fuzzy aggregation operators. Comput Appl Math 40(1):16

    Article  MathSciNet  MATH  Google Scholar 

  • Maclaurin C (1729) A second letter to Martin Folkes, Esq concerning the roots of equations, with demonstration of other rules of algebra Philos Trans Roy Soc London Ser A. 36:59–96

  • Mahboob A, Rashid T (2020) Multistage Decision Approach for Short Life Cycle Products Using Pythagorean. Fuzzy Set J Intell Fuzzy Syst 40(1):1343–1356

    Article  Google Scholar 

  • Mohagheghi V, Mousavi SM, Mojtahedi M, Newton S (2020) Evaluating large, high-technology project portfolios using a novel interval-valued Pythagorean fuzzy set framework: an automated crane project case study. Expert Syst Appl. 162:113007

    Article  Google Scholar 

  • Mu ZM, Zeng SZ, Wang PY (2021) Novel approach to multi-attribute group decision-making based on interval-valued Pythagorean fuzzy power Maclaurin symmetric mean operator. Comput Ind Eng 155:107049

    Article  Google Scholar 

  • Muhammad A, Sumera N, Edalatpanah SA, Rida M (2021a) Group decision-making framework under linguistic q-rung orthopair fuzzy Einstein models. Soft Comput 25(15):10309–10334

    Article  Google Scholar 

  • Muhammad Q, Saleem A, Liu Y, Muhammad N (2021) Multi-criteria decision support systems based on linguistic intuitionistic cubic fuzzy aggregation operators. J Amb Intel Hum Comp 12(8):8285–8303

    Article  Google Scholar 

  • Muhammad R, Anam H, Muhammad J K, Poom K (2021) Correlation coefficients for cubic bipolar fuzzy sets with applications to pattern recognition and clustering analysis IEEE Access 1

  • Pranjal T, Palash D (2021) Distance measures for cubic pythagorean fuzzy sets and its applications to multicriteria decision making. Granular Comput 6(2):1–18

    Google Scholar 

  • Qi M, Yang Z, Ren W, Wang H (2019) Lorentzian knowledge measures for atanassov’s intuitionistic fuzzy sets. J Intell Fuzzy Syst 36(1):473–486

    Article  Google Scholar 

  • Qin JD, Liu XW (2015) approaches to uncertain linguistic multiple attribute decision making based on dual maclaurin symmetric mean. J Intell Fuzzy Syst 29(1):171–186

    Article  MathSciNet  MATH  Google Scholar 

  • Qin YC, Cui XL, Huang MF, Zhong YR, Tang ZM, Shi PZ (2021) Multiple-attribute decision-making based on picture fuzzy archimedean power maclaurin symmetric mean operators. Granular Comput 6(3):737–761

    Article  Google Scholar 

  • Rong Y, Liu Y, Pei Z (2020) Complex q-rung orthopair fuzzy 2-tuple linguistic Maclaurin symmetric mean operators and its application to emergency program selection. Int J Intell Syst 35(11):1749–1790

    Article  Google Scholar 

  • Sanum A, Saleem A, Fazal G, Muhammad Q, Muhammad YK (2021) Cubic fuzzy Heronian mean Dombi aggregation operators and their application on multi-attribute decision-making problem. Soft Comput Fusion Found Methodol Appl 25(6):4175–4189

    Google Scholar 

  • Talukdar P, Dutta P(2021) Distance measures for cubic Pythagorean fuzzy sets and its applications to multicriteria decision making. Granular Comput 6(2)

  • Xu WH, Shang XP, Wang J (2021) Multiple attribute group decision-making based on cubic linguistic pythagorean fuzzy sets and power Hamy mean. Complex Intell Syst 7(3):1673–1693

    Article  Google Scholar 

  • Yager RR (2017) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222–1230

    Article  Google Scholar 

  • Yager R R (2013) Pythagorean fuzzy subsets. In: Proc. Joint IFSA World Congress and NAFIPS Annual Meeting 57–61

  • Zadeh LA (1965) Fuzzy sets. Inf. Control 8(3):338–353

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang ZM, Chen SYM (2021) Group decision making with incomplete q-rung orthopair fuzzy preference relations. Inf Sci 553:376–396

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang Q, Hu JH, Feng JF, Liu A (2020a) Multiple criteria decision making method based on the new similarity measures of Pythagorean fuzzy set. J Intell Fuzzy Syst 39(1):809–820

    Article  Google Scholar 

  • Zhang MY, Zheng TT, Zheng WR, Zhou LG (2020) Interval-valued pythagorean hesitant fuzzy set and its application to multiattribute group decision-making. Complexity 2020:1–26

    Google Scholar 

  • Zhong YR, Cao LB, Zhang HN, Qin YC, Huang MF, Luo XN (2021) Hesitant fuzzy power Maclaurin symmetric mean operators in the framework of Dempster–Shafer theory for multiple criteria decision making J Amb Intel Hum Comp

Download references

Acknowledgements

This article was supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No.KJQN201901505).

Funding

This article was supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN201901505), Key Project of humanities and social sciences research of Chongqing Municipal Education Commission in 2022(Grant No:22SKGH432), Key Project of humanities and social sciences research of Chongqing Municipal Education Commission in 2022(Grant No:22SKGH428).

Author information

Authors and Affiliations

  1. School of Business and Administration, Chongqing University of Science and Technology, Chongqing, 401331, China

    Qian Yu, Jun Cao, Ling Tan, Ya Liao & Jiongyan Liu

Authors
  1. Qian Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jun Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ling Tan
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Ya Liao
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Jiongyan Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Qian Yu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, Q., Cao, J., Tan, L. et al. Multiple attribute decision-making based on maclaurin symmetric mean operators on q-rung orthopair cubic fuzzy sets. Soft Comput 26, 9953–9977 (2022). https://doi.org/10.1007/s00500-022-07363-7

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-022-07363-7

Keywords