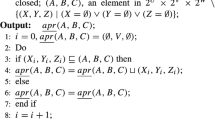Abstract
Rough set theory is an extension of set theory with two additional unary set-theoretic operators known as approximation in order to extract information and knowledge. It needs the basic, or say definable, knowledge to approximate the undefinable knowledge in a knowledge space using the pair of approximation operators. Many existed approximation operators are expressed with unary form. How to mine the knowledge which is asked by binary form with rough set has received less research attention, though there are strong needs to reveal the answer for this challenging problem. There exist many information with matroid constraints since matroid provides a platform for combinatorial algorithms especially greedy algorithm. Hence, it is necessary to consider a matroidal structure on two sets no matter the two sets are the same or not. In this paper, we investigate the construction of approximation operators expressed by binary form with matroid theory, and the constructions of matroidal structure aided by a pair of approximation operators expressed by binary form.
-
First, we provide a kind of matroidal structure—TD-matroid defined on two sets as a generalization of Whitney classical matroid.
-
Second, we introduce this new matroidal construction to rough set and construct a pair of approximation operators expressed with binary form.
-
Third, using the existed pair of approximation operators expressed with binary form, we build up two concrete TD-matroids.
-
Fourth, for TD-matroid and the approximation operators expressed by binary form on two sets, we seek out their properties with aspect of posets, respectively.
-
Through the paper, we use some biological examples to explain and test the correct of obtained results. In summary, this paper provides a new approach to research rough set theory and matroid theory on two sets, and to study on their applications each other.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data Availability
All of authors confirm that this statement is accurate.
References
Acharjya DP, Ahmed NSS (2020) Tracing of online assaults in 5G networks using dominance based rough set and formal concept analysis. Peer Peer Netw Appl 14(1):349–374. https://doi.org/10.1007/s12083-020-00983-6
Ambadi N (2019) Insights into netword coding using tools from linear algebra and matroid theory. Ph.D. Thesis, Indian Institute of Science, India, Bengaluru
Apolloni B (2021) Inferring statistical trends of the COVID19 pandemic from current data. Where probability meets fuzziness. Inf Sci 574:333–348. https://doi.org/10.1016/j.ins.2021.06.011
Błaszczyński J, Filho ATA, Matuszyk A, Szela̧g M, Słowiński R (2021) Auto loan fraud detection using dominance-based rough set approach versus machine learning methods. Expert Syst Appl 163:113740. https://doi.org/10.1016/j.eswa.2020.113740
Bonikowski Z, Bryniarski E, Wybrazjec-Skardowska U (1998) Extensions and intentions in the rough set theory. Inf Sci 107:149–167. https://doi.org/10.1016/s0020-0255(97)10046-9
Cattanco G (1998) Abstract approximation spaces for rough theories. In: Polkowski L, Skowron A (eds) Rough sets in knowledge discovery 1: methodology and applications (studies in fuzziness and soft computing). Physica-Verlag, Heidelberg, pp 59–98. https://doi.org/10.1109/NAFIPS.2006.365437
Corah M, Michael N (2019) Distributed matroid-constrained submodular maximization for multi-robot exploration: theory and practice. Auton Robots 43:485–501. https://doi.org/10.1007/s10514-018-9778-6
Ganter B, Wille R (1999) Formal concept analysis: mathematical foundations. Springer, Berlin. https://doi.org/10.1007/978-3-642-59830-2
Grätzer G (2011) Lattice theory: foundation. Springer, Basel. https://doi.org/10.1007/978-3-0348-0018-1
He FZ, Shi JP (2019) Diversified recommendation approach under non-uniform partition matroid constraints. J Front Comput Sci Tech 13(2):226–238. https://doi.org/10.3778/j.issn.1673-9418.1803021 (in Chinese with English summary)
Hou Q, Clark A (2021) Robust maximization of correlated submodular functions under cardinality and matroid constraints. IEEE Trans Autom Control 66(12):6148–6155. https://doi.org/10.1109/TAC.2021.3061656
Hu MJ, Yao YY (2019) Structured approximations as a basis for three-way decisions in rough set theory. Knowl Based Syst 165:92–109. https://doi.org/10.1016/j.knosys.2018.11.022
Huang AP, Zhu W (2016) Connectedness of graphs and its application to connected matroids through covering-based rough sets. Soft Comput 20:1841–1851. https://doi.org/10.1007/s00500-015-1859-2
Im S, Moseley B, Zhou R (2021) The matroid cup game. Oper Res Lett 49(3):405–411. https://doi.org/10.1016/j.orl.2021.04.005
Kauser AP, Acharjya PD (2021) Knowledge inferencing using artificial bee colony and rough set for diagnosis of hepatitis disease. Int J Health Inf Syst Inform 16(2):49–72. https://doi.org/10.4018/IJHISI.20210401.oa3
Kleinberg R, Weinberg SM (2019) Matroid prophet inequalities and applications to multi-dimensional mechanism design. Games Econ Behav. https://doi.org/10.1016/j.geb.2014.11.002
Lei L, Chen W, Wu B, Chen C, Liu W (2021) A building energy consumption prediction model based on rough set theory and deep learning algorithms. Energ Build 240:110886. https://doi.org/10.1016/j.enbuild.2021.110886
Li XN (2019) Three-way fuzzy matroids and granular computing. Int J Approx Reason 114:44–50. https://doi.org/10.1016/j.ijar.2019.08.003
Li XN, Liu SY (2012) Matroidal approaches to rough sets via closure operators. Int J Approx Reason 53:513–527. https://doi.org/10.1016/j.ijar.2011.12.005
Li XN, Yi HJ, Liu SY (2016) Rough sets and matroids from a lattice-theoretic viewpoint. Inf Sci 342:37–52. https://doi.org/10.1016/j.ins.2016.01.029
Li XN, Sun BZ, She YH (2017) Generalized matroids based on three-way decision models. Int J Approx Reason 90:192–207. https://doi.org/10.1016/j.ijar.2017.07.012
Li XN, Yi HJ, Wang ZH (2019) Approximation via a double-matroid structure. Soft Comput 23:7557–7568
Liu SS, Dong SH, Ren GD (2011) Phylogenetic relationships of Uloma in China. J Hebei Univ (Natl Sci Ed) 31(4):427–433 ((in Chinese with English summary))
Liu S, Manganiello F, Kschischang FR (2017) Matroidal structure of skew polynomial rings with application to network coding. Finite Fields Their Appl 46:236–246. https://doi.org/10.1016/j.ffa.2017.04.007
Mao H (2018) Concept lattices and simple matroids. Acta Math Appl Sin 41(3):347–355 ((in Chinese with English summary))
Mao H (2019) Approximation operators for semiconcepts. J Intell Fuzzy Syst 36:3333–3343. https://doi.org/10.3233/JIFS-18104
Mao H, Hu MJ, Yao YY (2021) Algebraic approaches to granular computing. Granul Comput 6:119–131. https://doi.org/10.1007/s41066-019-00178-2
Marek VW, Skowron A (2014) Rough sets and matroids. In: Peters JF, Skowron A (eds) Transactions on rough sets XVII. Springer, Berlin, pp 74–81. https://doi.org/10.1007/978-3-642-54756-0_4
Mi JS, Leung Y, Zhao HY, Feng T (2008) Generalized fuzzy rough sets determined by triangular norm. Inf Sci 178:3203–3213. https://doi.org/10.1016/j.ins.2008.03.013
Oxley J (2011) Matroid theory, 2nd edn. Oxford University Press, New York. https://doi.org/10.1093/acprof:oso/9780198566946.001.0001
Pawlak Z (1982) Rough sets. Int J Comput Inf Sci 11:341–356. https://doi.org/10.1007/BF01001956
Pawlak Z (1991) Rough sets: theoretical aspects of reasoning about data. Kluwer Academic Publishers, Dordrecht. https://doi.org/10.1007/978-94-011-3534-4
Pawlak Z, Skowron A (2007a) Rudiments of rough sets. Inf Sci 177(1):3–27. https://doi.org/10.1016/j.ins.2006.06.003
Pawlak Z, Skowron A (2007b) Rough sets: some extensions. Inf Sci 177(1):28–40. https://doi.org/10.1016/j.ins.2006.06.006
Pawlak Z, Skowron A (2007c) Rough sets and Boolena reasoning. Inf Sci 177(1):41–73. https://doi.org/10.1016/j.ins.2006.06.007
Pedrycz W, Bargiela A (2002) Granular clustering: a granular signature of data. IEEE Trans Syst Man Cybern B 32(2):212–224. https://doi.org/10.1109/3477.990878
Pei DW, Xu ZB (2004) Rough set models on two universes. Int J Gen Syst 33(5):569–581. https://doi.org/10.1080/0308107042000193561
Penmatsa RKV, Kalidindi A, Mallidi SKR (2020) Feature reduction and optimization of malware detection system using ant colony optimization and rough sets. Int J Inf Secur Priv 14(3):95–114. https://doi.org/10.4018/IJISP.2020070106
Qu JH, Bai X, Gu JJ, Taghizadeh-Hesary F, Lin J (2020) Assessment of rough set theory in relation to risks regarding hydraulic engineering investment decisions. Mathematics 8(8):1308. https://doi.org/10.3390/math8081308
Restrepo M, Aguilar JF (2019) Matroids and submodular functions for covering-based rough sets. In: Bello R, Falcon R, Verdegay J (eds) Uncertainty management with fuzzy and rough sets. Studies in fuzziness and soft computing, vol 377. Springer, Cham, pp 175–191. https://doi.org/10.1007/978-3-030-10463-4_10
Selvi S, Chandrasekaran M (2019) Framework to forecast environment changes by optimized predictive modelling based on rough set and Elman neural network. Soft Comput 24(14):10467–10480. https://doi.org/10.1007/s00500-019-04556-5
Shang L, Wang YL, Wang PP (2010) Application of rough set analysis in species and caste discrimination of Bumblebees (Hymenoptera: Apidae: Bombus) based on antennal sensilla. Ann Entomol Soc Am 103(4):654–660. https://doi.org/10.1603/AN10017
Shao MW, Guo L, Wang CZ (2018) Connections between two-universe rough sets and formal concept. Int J Mach Learn Cybern 9:1869–1877. https://doi.org/10.1007/s13042-018-0803-z
Silfia A, Rianto S, Anjar W, Harly O, Daengs GSA, Solly A (2021) Utilization of rough sets method with optimization genetic algorithms in heart failure cases. J Phys Conf Ser 1933:012038. https://doi.org/10.1088/1742-6596/1933/1/012038
Sinha AK, Namdev N (2020) Computational approach of tumor growth in human body with a significant technique the rough set. IOP Conf Ser Mater Sci Eng 798:012038. https://doi.org/10.1088/1757-899X/798/1/012038
Stefanutti L (2019) On the assessment of procedural knowledge: from problem spaces to knowledge spaces. Br J Math Stat Psychol 72(2):185–218. https://doi.org/10.1111/bmsp.12139
Sun BZ, Ma WM, Qian YH (2017) Multigranulation fuzzy rough set over two universes and its applications to decision making. Knowl Based Syst 123:61–74. https://doi.org/10.1016/j.knosys.2017.01.036
Vormbrock B, Wille R (2005) Semiconcept and protoconcept algebras: the basic theorems. In: Ganter B, Stumme G, Wille R (eds) Formal concept analysis: foundations and applications. Springer, Berlin, pp 34–48. https://doi.org/10.1007/11528784_2
Wang G, Mao H (2020) Approximation operators based on preconcepts. Open Math 18(1):400–416. https://doi.org/10.1515/math-2020-0146
Wang ZH, Feng QR, Wang H (2019) The lattice and matroid representations of definable sets in generalized rough sets based on relations. Inf Sci 485:505–520. https://doi.org/10.1016/j.ins.2019.02.034
Wang G, Mao H, Wu ZY (2020) Application of Galois connection in constructing matroids. Comput Eng Sci 42(7):1276–1286. https://doi.org/10.3969/j.issn.1007-130X.2020.07.017 (in Chinese with English summary)
Wang GQ, Li TR, Zhang PF, Huang QQ, Chen HM (2021) Double-local rough sets for efficient data mining. Inf Sci 571:475–498. https://doi.org/10.1016/j.ins.2021.05.007
Watt JH, Berg SVD (2002) Research methods for communication science. Allyn and Bacon, Boston
Wei MH, Zheng ZH, Bai X, Lin J, Taghizadeh HF (2021) Application of rough set and neural network in water energy utilization. Front Energy Res 9:604660. https://doi.org/10.3389/fenrg.2021.604660
Welsh DJA (1976) Matroid theory. Academic Press Inc., London. https://doi.org/10.1007/978-1-4612-9914-1_10
Whitney H (1935) On the abstract properties of linear dependence. Am J Math 57:509–533. https://doi.org/10.1007/978-1-4612-2972-8_10
Xu FF, Yao YY, Miao DQ (2008) Rough set approximations in formal concept analysis and knowledge spaces. In: ISMIS 2008. LNAT, 4994:319-328 https://doi.org/10.1007/978-3-540-68123-6_35
Xu TH, Wang GY (2018) Finding strongly connected components of simple digraphs based on generalized rough sets theory. Knowl Based Syst 149:88–98. https://doi.org/10.1016/j.knosys.2018.02.038
Yao YY (2001) Information granulation and rough set approximation. Int J Intel Syst 16:87–104. https://doi.org/10.1002/1098-111x(200101)16:1$<$87::aid-int7$>$3.0.co;2-s
Yao YY, Yao BX (2012) Covering based rough set approximations. Inf Sci 200:91-107 https://doi.org/10.1016/j.ins.2012.02.065https://doi.org/10.1016/j.knosys.2018.08.023
Yao YY (1996) Two views of the theory of rough sets in finite universes. Int J Approx Reason 15:291–317. https://doi.org/10.1016/S0888-613X(96)00071-0
Yao YY (1998a) Relational interpretations of neighborhood operators and rough set approximation operators. Inf Sci 101:239–259. https://doi.org/10.1016/S0020-0255(98)10006-3
Yao YY (1998b) Generalized rough set models. In: Polkowski L, Skowron A (eds) Rough sets in knowledge discovery. Physica-Verlag, Heidelberg, pp 286–318. https://doi.org/10.1007/978-3-540-72458-2_1
Yao YY (2015) The two sides of the theory of rough sets. Knowl Based Syst 80:67–77. https://doi.org/10.1016/j.knosys.2015.01.004
Yao YY, Wong S, Wang L (1995) A non-numeric approach to uncertain reasoning. Int J Gen Syst 23:343–359. https://doi.org/10.1080/03081079508908047
Yao W, She YH, Lu LX (2019) Metric-based L-fuzzy rough sets: approximation operators and definable sets. Knowl Based Syst 163:91–102
Yoshifumi K, Jerzy B, Masahiro I, Roman S (2021) Empirical risk minimization for dominance-based rough set approaches. Inf Sci 567:395–417. https://doi.org/10.1016/j.ins.2021.02.043
Ytow N, Morse DR, Roberts DM (2006) Rough set approximation as formal concept. J Adv Comput Intel Intel Inf 10(5):606–611
Zhang X, Miao D, Liu C, Le M (2016) Constructive methods of rough approximation operators and multigranulation rough sets. Knowl Based Syst 91:114–125. https://doi.org/10.1016/j.knosys.2015.09.036
Zhang YL, Li CQ, Li JJ (2019) On characterizations of a pair of covering-based approximation operators. Soft Comput 23(12):3965–3972. https://doi.org/10.1007/s00500-018-3321-8
Zhao XR, Hu BQ (2020) Three-way decisions with decision-theoretic rough sets in multiset-valued information tables. Inf Sci 507:684–699. https://doi.org/10.1016/j.ins.2018.08.024
Zhu W, Wang SP (2011) Matroidal approaches to generalized rough sets based on relations. Int J Mach Learn Cybern 2:273–279. https://doi.org/10.1007/s13042-011-0027-y
Zhu P, Hu H, Zhang Y, Li XT (2021) Enhancing traceability of infectious diseases: a blockchain-based approach. Inform Process Manag 58:102570. https://doi.org/10.1016/j.ipm.2021.102570
Acknowledgements
The authors sincerely thank the anonymous referees for their valuable comments and suggestions on this paper.
Funding
This study was funded by National Natural Science Foundation of China (grant number 61572011); Nature Science Foundation of Hebei Province (Grant Number A2018201117)
Author information
Authors and Affiliations
Contributions
Gang Wang: All of methods are used to biology, data curates, writing—review & editing. Hua Mao helped in conceptualization, methodology, writing—original draft.
Corresponding author
Ethics declarations
Conflict of interest
Author Hua Mao has received research grants from NNSF of China. All of authors have received research grants from NSF of Hebei Province, China. All of authors declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
1. Proof of Lemma 7
Proof
Let \(low(A,B)=\{(X_j,Y_j), j\in \mathcal {J}\}\) and \(upr(A,B)=\{(X_p, Y_p), p\in \mathcal {P}\}\). It follows \(|\mathcal {J}|, |\mathcal {P}|<\infty \) since \(|S|,|T|<\infty \).
Next, we prove item (1).
\(X_j\subseteq A\) and \(B\subseteq Y_j\) hold since \((X_j,Y_j)\sqsubseteq (A,B) \; (j\in \mathcal {J})\). So, we obtain \(\cup _{j\in \mathcal {J}}X_j\subseteq A\) and \(B\subseteq \cap _{j\in \mathcal {J}}Y_j\). And further, we get \(\underline{MR}(A,B)=(\cup _{j\in \mathcal {J}}X_j, \cap _{j\in \mathcal {J}} Y_j)\sqsubseteq (A,B)\).
If \(|\mathcal {P}|=0\), then \(upr(A,B)=\emptyset \). Under this case, we know \(\overline{MR}(A,B)=(S,\emptyset )\) by Definition 8. So, \((A,B)\sqsubseteq \overline{MR}(A,B)\) holds since \(A\subseteq S\) and \(B\supseteq \emptyset \).
If \(|\mathcal {P}|\ne \emptyset \), then \(A\subseteq X_p\) and \(B\supseteq Y_p\) hold since \((A,B)\sqsubseteq (X_p,Y_p)\;(p\in \mathcal {P})\). So, we obtain \(A\subseteq \cap _{p\in \mathcal {P}}X_p\) and \(B\supseteq \cup _{p\in \mathcal {P}}Y_p\). And further, we get \((A,B)\sqsubseteq (\cap _{p\in \mathcal {P}}X_p, \cup _{p\in \mathcal {P}} Y_p)=\overline{MR}(A,B)\).
Next, we prove item (2).
Let \((A,B)\in \mathcal {T}\). Then, \(A\subseteq A\) and \(B\subseteq B\) together mean \((A,B)\in low(A,B)\) and \((A,B)\in upr(A,B)\).
On the one hand, there is one and only one \(j_0\in \mathcal {J}\) satisfying \(X_{j_0}=A\) and \(Y_{j_0}=B\) since \((A,B)\in low(A,B)\). So, we get \(A=X_{j_0}\subseteq \cup _{j\in \mathcal {J}}X_j\subseteq A\) and \(B=Y_{j_0}\supseteq \cap _{j\in \mathcal {J}}Y_j\supseteq B\) according to the definition of \(\underline{MR}(A,B)\) and item (1). Thus, we obtain \(\underline{MR}(A,B)=(\cup _{j\in \mathcal {J}}X_j,\cap _{j\in \mathcal {J}}Y_j)=(A,B)\).
On the other hand, there is one and only one \(p_0\in \mathcal {P}\) satisfying \(X_{p_0}=A\) and \(Y_{p_0}=B\) since \((A,B)\in upr(A,B)\). So, we get \(A\subseteq \cap _{p\in \mathcal {P}}X_p\subseteq X_{p_0}=A\) and \(B\supseteq \cup _{p\in \mathcal {P}}Y_p\supseteq Y_{p_0}=B\) according to the definition of \(\overline{MR}(A,B)\) and item (1). Thus, we obtain \(\overline{MR}(A, B)=(\cap _{p\in \mathcal {P}}X_p,\cup _{p\in \mathcal {P}}Y_p)=(A,B)\).
Next, we prove item (3).
Suppose \(\underline{MR}(A,B)=(A,B)=\overline{MR}(A,B)\). Then, it infers the following formulas
It induces \((A,Y_p)\sqsubseteq (X_p,Y_p)\in \mathcal {T}\) according to \(Y_p\subseteq Y_p\) and the formula \(\textcircled {1}\; (p\in \mathcal {P})\). Combining formula \(\textcircled {2}\) with (T2) and \((X_p,Y_p)\in \mathcal {T}\,(p\in \mathcal {P})\), we get \((A,Y_p)\in \mathcal {T}\) satisfying \((A,B)\sqsubseteq (A,Y_p)\) for any \(p\in \mathcal {P}\). Thus, \((A,Y_p)\in upr(A,B)\) holds for any \(p\in \mathcal {P}\). That is to say, there is \(p_1\in \mathcal {P}\) such that \(X_{p_1}=A\) satisfying \((X_{p_1}, Y_p)\in \mathcal {T}\, (p\in \mathcal {P})\). Additionally, \((X_p,B)\sqsubseteq (X_p,Y_p)\in \mathcal {T}\) holds since \(B\supseteq Y_p\) holds by formula \(\textcircled {2}\;(p\in \mathcal {P})\). Taking this result with (T2), it induces \((X_p,B)\in \mathcal {T}\,(p\in \mathcal {P})\). Combining formula \(\textcircled {1}\) with \((A,B)\sqsubseteq (X_p,B)\,(p\in \mathcal {P})\), we get \((X_p,B)\in upr(A,B)\) for any \(p\in \mathcal {P}\). That is to say, there is \(p_2\in \mathcal {P}\) such that \(Y_{p_2}=B\) and \((X_p, Y_{p_2})\in \mathcal {T}\, ( p\in \mathcal {P})\). Especially, \((X_{p_1}, Y_{p_2})\in \mathcal {T}\) holds since \(p_1\in \mathcal {P}\). In other words, \((A,B)\in \mathcal {T}\) is followed since \(X_{p_1}=A\) and \(Y_{p_2}=B\).
2. Proof of Lemma 8
Proof
Let \(low(A_i,B_i) =\{(X_{ij}, Y_{ij}), j\in \mathcal {J}_i\}\) and \(upr(A_i,B_i) =\{(X_{ip}, Y_{ip}), p\in \mathcal {P}_i\}\, (i=1,2)\).
To prove item (1).
\((X_{1j}, Y_{1j})\sqsubseteq (A_1,B_1)\sqsubseteq (A_2,B_2)\) follows \((X_{1j}, Y_{1j})\in low (A_2,B_2)\, (j\in \mathcal {J}_1)\). So, we get \(\cup _{j\in \mathcal {J}_1}X_{1j}\subseteq \cup _{j\in \mathcal {J}_2}X_{2j}\) and \(\cap _{j\in \mathcal {J}_1}Y_{1j}\supseteq \cap _{j\in \mathcal {J}_2}Y_{2j}\). Furthermore, we obtain \(\underline{MR}(A_1,B_1)=(\cup _{j\in \mathcal {J}_1}X_{1j}, \cap _{j\in \mathcal {J}_1}Y_{1j})\sqsubseteq (\cup _{j\in \mathcal {J}_2}X_{2j},\cap _{j\in \mathcal {J}_2}Y_{2j})=\underline{MR}(A_2,B_2)\).
To prove item (2).
\((A_1,B_1)\sqsubseteq (A_2,B_2)\sqsubseteq (X_{2p},Y_{2p})\) follows \((X_{2p},Y_{2p})\in upr(A_1,B_1)\,(p\in \mathcal {P}_2)\). So, \(upr(A_2,B_2)\subseteq upr(A_1,B_1)\) holds. This demonstrates that the case of \(upr(A_1,B_1)=\emptyset \) and \(upr(A_2,B_2)\ne \emptyset \) does not exist. In other words, it exists and only exists the following cases:
Case 1. \(upr(A_i,B_i)\ne \emptyset \,\, (i=1,2)\);
Case 2. \(upr(A_i,B_i)=\emptyset \,\, (i=1,2)\);
Case 3. \(upr(A_1,B_1)\ne \emptyset \) and \(upr(A_2,B_2)=\emptyset \).
Under Case 1, we get \(\cap _{p\in \mathcal {P}_1}X_{1p}\subseteq \cap _{p\in \mathcal {P}_2}X_{2p}\) and \(\cup _{p\in \mathcal {P}_1}Y_{1p}\supseteq \cup _{p\in \mathcal {P}_2}Y_{2p}\) according to \(upr(A_2,B_2)\subseteq upr(A_1,B_1)\). Furthermore, we obtain \(\overline{MR}(A_1,B_1)=(\cap _{p\in \mathcal {P}_1}X_{1p},\cup _{p\in \mathcal {P}_1}Y_{1p}) \sqsubseteq (\cap _{p\in \mathcal {P}_2}X_{2p},\cup _{p\in \mathcal {P}_2}Y_{2p}) = \overline{MR}(A_2,B_2)\).
Under Case 2, we obtain \(\overline{MR}(A_i,B_i)=(S,\emptyset )\, (i=1,2)\) in view of Definition 8. That is, \(\overline{MR}(A_1,B_1)\sqsubseteq \overline{MR}(A_2,B_2)\) holds.
Under Case 3, we obtain \(\overline{MR}(A_2,B_2)=(S,\emptyset )\) and the existence of \(\overline{MR}(A_1,B_1)\) with \((\overline{MR}(A_1,B_1)\ne (S,\emptyset )\) in light of Definition 8. It is easy to see \(\overline{MR}(A_1,B_1)\sqsubseteq (S,\emptyset )\). Namely, it has \(\overline{MR}(A_1,B_1)\sqsubseteq \overline{MR}(A_2,B_2)\).
3. Proof of Theorem 3(2)
Proof
Since \(\mathbb {K}\) is a formal context, it follows \(O\ne \emptyset \) and \(P\ne \emptyset \) by Definition 2. Using Definition 7, we only need to check the conditions (T1), (T2) and (T3) to be satisfied by \(\overline{\mathcal {T}_{(A,B)}}(R)\), respectively.
First to check (T1) for \(\overline{\mathcal {T}_{(A,B)}}(R)\).
Using Lemma 2(1), we receive \(\overline{R}(\emptyset , B)=(\emptyset , \emptyset ^\prime \cup B)=(\emptyset , P)\) since \(\emptyset ^\prime =P\) for \(\emptyset \subseteq O\). Hence, \((\emptyset , B)\in \overline{\mathcal {T}_{(A,B)}}(R)\) holds since \(\emptyset \subseteq A\) and \(P\supseteq B\) together follow \((\emptyset , P)\sqsubseteq (A,B)\). Thus, \(\overline{\mathcal {T}_{(A,B)}}(R)\ne \emptyset \) holds.
Second to check (T2) for \(\overline{\mathcal {T}_{(A,B)}}(R)\).
Let \((X_2,Y_2)\sqsubseteq (X_1,Y_1)\in \overline{\mathcal {T}_{(A,B)}}(R)\). Then, we may easily find \(X_2\subseteq X_1\) and \(Y_2\supseteq Y_1\) by the definition of \(\sqsubseteq \). In addition, we also find the following two facts.
Combining the above two facts and \(X_2\subseteq X_1\subseteq A\), we obtain \(X_2^\prime \cup Y_2\supseteq X_1^\prime \cup Y_1\supseteq B\). Thus, \(\overline{R}(X_2,Y_2)=(X_2,X_2^\prime \cup Y_2)\sqsubseteq (A,B)\) holds. So, \((X_2,Y_2)\in \overline{\mathcal {T}_{(A,B)}}(R)\) is followed.
Third to check (T3) for \(\overline{\mathcal {T}_{(A,B)}}(R)\).
Let \((X_1,Y_1), (X_2,Y_2)\in \overline{\mathcal {T}_{(A,B)}}(R)\) satisfy \(|(X_2,Y_2)|<|(X_1,Y_1)|\) and \((X_1,Y_1)\ne (\emptyset ,\emptyset )\). Then, we get the following fact:
Via Lemma 4, we confirm \((X_1,Y_1){\setminus }(X_2,Y_2)\ne (\emptyset ,\emptyset )\). Then, we select \((a,b)\in (X_1,Y_1)\setminus (X_2,Y_2)\). We divide two cases to finish the proof.
Case 1. \(X_1\setminus X_2=\emptyset \).
It gets \(a=\emptyset \) and \(b\in Y_1{\setminus } Y_2\ne \emptyset \). Then, we obtain \(\overline{R}((X_2,Y_2)\cup (a,b))=\overline{R}(X_2, Y_2\cup b )= (X_2,(X_2^\prime \cup Y_2)\cup b )\) holds according to Lemma 2(1). Using \(X_2^\prime \cup Y_2\supseteq B\), we obtain \((X_2^\prime \cup Y_2)\cup b \supseteq B\). Thus, combining \(X_2\subseteq A\) with the results mentioned above, we confirm \(\overline{R}((X_2,Y_2)\cup (a,b))\sqsubseteq (A,B)\). Hence, we receive \((X_2,Y_2)\cup (a,b)\in \overline{\mathcal {T}_{(A,B)}}(R)\).
Case 2. \(X_1\setminus X_2\ne \emptyset \).
Select \(a\in X_1{\setminus } X_2\) and \(b\in Y_1{\setminus } Y_2\). If \(Y_1{\setminus } Y_2=\emptyset \) (or \(Y_1{\setminus } Y_2\ne \emptyset \)), then \(b=\emptyset \) (or \(b\ne \emptyset \)). No matter which situation happens, it follows
Combining \(a\in X_1\subseteq A\) and \(X_2\subseteq A\), we obtain \(X_2\cup a \subseteq X_2\cup X_1\subseteq A\). So, \((X_2\cup a )^\prime =X_2^\prime \cap a^\prime \supseteq A^\prime \) in light of Lemma 1. Thus, we confirm \((X_2^\prime \cap a^\prime )\cup (Y_2\cup b )\supseteq A^\prime \cup (Y_2\cup b)\supseteq A^\prime \supseteq B\) since \(B\subseteq A^\prime \). Furthermore, we get \((X_2,Y_2)\cup (a,b)\in \overline{\mathcal {T}_{(A,B)}}(R)\).
Summing up the above two cases, (T3) is correct for \(\overline{\mathcal {T}_{(A,B)}}(R)\).
4. Proofs of items (2), (3) and (4) in Theorem 4
Proof
The proof of item (2) will be finished by two parts.
To prove item (3).
Combining Remark 2, we know \(\emptyset ^\prime =P\) for \(\emptyset \subseteq O\). This implies \((\emptyset ,P)\in \mathcal {B}(\mathbb {K})\) by Definition 2(2) and Remark 2. So, it infers \(\underline{R}(\emptyset ,P)=\overline{R}(\emptyset ,P)=(\emptyset ,P)\) using Lemma 2(4).
It is clear \((\emptyset , P)\sqsubseteq (A,B)\). Moreover, we receive \((\emptyset , P)\in \underline{\mathcal {T}_{(A,B)}}(R)\) and \((\emptyset , P)\in \overline{\mathcal {T}_{(A,B)}}(R)\). Additionally, both \((\emptyset ,P)\sqsubseteq (X_j,Y_j)\) and \((\emptyset ,P)\sqsubseteq (X_p,Y_p)\) evidently hold \((j\in \mathcal {J};p\in \mathcal {P})\). Considered item (1), we can indicate \((\emptyset ,P)\) to be the minimum element in the poset \((\underline{\mathcal {T}_{A,B)}}(R),\sqsubseteq )\), and also the minimum element in the poset \((\overline{\mathcal {T}_{(A,B)}}(R),\sqsubseteq )\).
Additionally, we obtain the following expression Part I.
Using the definition of \(\sqsubseteq \), we may easily obtain “\(X_j\subseteq \cup _{j\in \mathcal {J}}X_j\) and \(Y_j\supseteq \cap _{j\in \mathcal {J}}Y_j\)”\(\Rightarrow ``(X_j,Y_j)\sqsubseteq (\cup _{j\in \mathcal {J}}X_j,\cap _{j\in \mathcal {J}}Y_j)\)” for any \(j\in \mathcal {J}\). Considered this result with the result in Part I, we find \((\cup _{j\in \mathcal {J}}X_j,\cap _{j\in \mathcal {J}}Y_j)\) to be the maximum element in \((\underline{\mathcal {T}_{(A,B)}}(R),\sqsubseteq )\).
We can obtain the following expression Part II.
Using the definition of \(\sqsubseteq \), we may easily obtain “\(X_p\subseteq \cup _{p\in \mathcal {P}}X_p\) and \(Y_p\supseteq \cap _{p\in \mathcal {P}}Y_p\)”\(\Rightarrow ``(X_p,Y_p)\sqsubseteq (\cup _{p\in \mathcal {P}}X_p,\cap _{p\in \mathcal {P}}Y_p)\)” for any \(p\in \mathcal {P}\). Combining the result of Part II with the above result, we find \((\cup _{p\in \mathcal {P}}X_p,\cap _{p\in \mathcal {P}}Y_p)\) to be the maximum element in \((\overline{\mathcal {T}_{(A,B)}}(R),\sqsubseteq )\).
To prove item (4).
We will use two parts to finish the proof.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wang, G., Mao, H. Approximation operators via TD-matroids on two sets. Soft Comput 26, 9785–9804 (2022). https://doi.org/10.1007/s00500-022-07367-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-022-07367-3