An extensive operational law for monotone functions of LR fuzzy intervals with applications to fuzzy optimization

Abstract

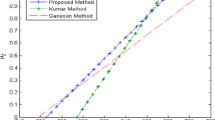
The operational law proposed by Zhou et al. (J Intell Fuzzy Syst 30(1): 71–87, 2016) contributes to developing fuzzy arithmetic, while its applicable conditions are confined to strictly monotone functions and regular LR fuzzy numbers, which are hindering their operational law from dealing with more general cases, such as problems formulated as monotone functions and problems with fuzzy variables represented as fuzzy intervals (e.g., trapezoidal fuzzy numbers). In order to handle such cases we generalize the operational law of Zhou et al. in both the monotonicity of function and fuzzy variables in this paper and then apply the extensive operational law to the cases with monotone (but not necessarily strictly monotone) functions with regard to regular LR fuzzy intervals (LR-FIs) (of which regular LR fuzzy numbers are special cases). Specifically, we derive the computational formulae for expected values (EVs) of LR-FIs and monotone functions with regard to regular LR-FIs, respectively. On the other hand, we develop a solution scheme to dispose of fuzzy optimization problems with regular LR-FIs, in which a fuzzy programming is converted to a deterministic equivalent one and a newly devised solution algorithm is utilized to get the deterministic programming solved. The numerical experiments are conducted using our proposed solution scheme and the traditional fuzzy simulation-based genetic algorithm in the context of a purchasing planning problem. Computational results show that our method is much more efficient, yielding high-quality solutions.

Appendices

The abbreviations

The proof of Theorem 1

Proof

For the case of $\delta =0$, we have $\mathrm{Cr}\{\zeta \le \psi ^{-1}(0)\}=\mathrm{Cr}\{\zeta \le \sup \{t | \psi (t)=0\}\}=0$, thus Eq. (5) holds.

For any $\delta \in (0,1)$ and $\delta \in D_\psi$, it is obvious that there should be at least one point $t_0$ makes $\psi (t_0)=\delta$ holds. Thus $\mathrm{Cr}\{\zeta \le t_0\}=\delta$ holds for any $t_0\in \{t | \psi (t)=\delta \}$, that is, $\mathrm{Cr}\{\zeta \le f_\delta \}=\delta$ holds for $f_\delta \in \psi ^{-1}(\delta )$. It is not difficult to find that $\sup \{\gamma | \psi ^{-1}(\gamma )=\psi ^{-1}(\delta )\}=\delta$. Equation  (5) is proved.

Table 7 The abbreviations are used in this manuscript

If $\delta \in (0,1)$ and $\alpha \delta \notin D_\Psi$, in the light of Eq. (6), we can get $\mathrm{Cr}\{\zeta \le \psi ^{-1}(\delta )\}=\mathrm{Cr}\{\zeta \le \inf \{t | \psi (t)\ge \delta \}\}$. Let $\mathrm{Cr}\{\zeta \le \inf \{t | \psi (t)\ge \delta \}\}=\overline{\delta }$. Then we have $\overline{\delta }=\sup \{\gamma | \psi ^{-1}(\gamma )=\psi ^{-1}(\delta )\}$. Equation  (5) holds.

If $\delta =1$, $\mathrm{Cr}\{\zeta \le \psi ^{-1}(1)\}=\mathrm{Cr}\{\zeta \le \inf \{t | \psi (t)$ $=1\}\}=1$. Eq. (5) is proved.

In the light of Definition 3, $\psi ^{-1}(\delta )$ is the ICD of $\zeta$. $\square$

The proof of Theorem 4

Proof

For simplicity, we just consider the situation of $n=2$. Assume that

$$\begin{aligned} \zeta =f(\zeta _1, \zeta _2), \end{aligned}$$

where $f(\zeta _1, \zeta _2)$ is increasing for $\zeta _1$ and decreasing for $\zeta _2$. In addition, suppose that

$$\begin{aligned} \begin{array}{rl} f(t_1, t_2)=s_0, \,\forall \,(t_1,t_2)\in \{(t_1,t_2)|\underline{\delta }\le R_1(\frac{t_1-\overline{c_1}}{\sigma _1})\\ \le \overline{\delta }, \underline{\delta }\le L_2(\frac{\underline{c_2}-t_2}{\rho _2})\le \overline{\delta }\} \end{array} \end{aligned}$$

where $s_0$ is a constant, $0<\underline{\delta }<\overline{\delta }<1$.

According to Zadeh’s extensive principal, we know that $\nu (s)=\sup \{\nu _1(t_1)\wedge \nu _2(t_2)| f(t_1, t_2)=s\}$. Since $f(\zeta _1, \zeta _2)$ is increasing for $\zeta _1$ and decreasing for $\zeta _2$, and $\zeta _1$ and $\zeta _2$ are regular LR-FIs, in view of Definition 1, we obtain that $\forall t_1\in \{t_1| L_1(\frac{\underline{c_1}-t_1}{\rho _1})\in (0,1)\}, t_2\in \{t_2| R_2(\frac{t_2-\overline{c_2}}{\sigma _2})\in (0,1)\},$

$$\begin{aligned} \nu (s)_{f(t_1,t_2)=s}=L_1\left( \frac{\underline{c_1}-t_1}{\rho _1}\right) =R_2\left( \frac{t_2-\overline{c_2}}{\sigma _2}\right) , \end{aligned}$$

and $\forall t_1\in \{t_1| R_1(\frac{t_1-\overline{c_1}}{\sigma _1})\in (0,\underline{\delta })\cup ( \overline{\delta },1)\}, t_2\in \{t_2| L_2(\frac{\underline{c_2}-t_2}{\rho _2})\in (0,\underline{\delta })\cup ( \overline{\delta },1)\},$

$$\begin{aligned} \nu (s)_{f(t_1,t_2)=s}=R_1\left( \frac{t_1-\underline{c_1}}{\sigma _1}\right) =L_2\left( \frac{\overline{c_2}-t_2}{\rho _2}\right) . \end{aligned}$$

Besides, it is easily known that $\nu (s_0)_{f(t_1,t_2)=s_0}=\overline{\delta }$ for $(t_1,t_2)\in \{(t_1,t_2)|\underline{\delta }\le R_1(\frac{t_1-\overline{c_1}}{\sigma _1})\le \overline{\delta },\underline{\delta }\le L_2(\frac{\underline{c_2}-t_2}{\rho _2})\le \overline{\delta }\}$. Based on the above analysis and Definition 1, we can get that $\zeta =f(\zeta _1, \zeta _2)$ is an LR-FI. $\square$

The proof of Theorem 5

Proof

According to Theorem 4, it is easily known that $\zeta$ is an LR-FI. Now we verify that Eq. (9) holds. For simplicity, we just verify the situation of $k=1$ and $n=2$. Assume that

$$\begin{aligned} \zeta =f(\zeta _1, \zeta _2), \end{aligned}$$

where f is increasing for $\zeta _1$ and decreasing for $\zeta _2$. In addition, suppose that

$$\begin{aligned} \psi ^{-1}(\delta )=f\left( \psi ^{-1}_1(\delta ), \psi ^{-1}_2(1-\delta )\right) , \end{aligned}$$

where $\psi _1^{-1}$ and $\psi _2^{-1}$ are the ICDs of $\zeta _1$ and $\zeta _2$, respectively. For each $\delta \in [0,1]$, it is defined that

$$\begin{aligned} \overline{\delta }= & {} \sup \Bigg \{\gamma \mid f\left( \psi ^{-1}_1(\gamma ), \psi ^{-1}_2(1-\gamma )\right) \nonumber \\= & {} f\left( \psi ^{-1}_1(\delta ), \psi ^{-1}_2(1-\delta )\right) \Bigg \}, \end{aligned}$$

(19)

which means that

$$\begin{aligned} f\left( \psi ^{-1}_1(\delta ), \psi ^{-1}_2(1-\delta )\right) =f\left( \psi ^{-1}_1(\overline{\delta }), \psi ^{-1}_2(1-\overline{\delta })\right) . \end{aligned}$$

(20)

We know that $\psi ^{-1}_1(\delta )$ and $\psi ^{-1}_2(1-\delta )$ are both intervals or both points, in which points can be considered as a special kind of intervals. Therefore, we only prove the case of intervals. The case of points can be verified similarly.

In view of Eq. (20), it is obvious that both $\psi ^{-1}_1(\overline{\delta })$ and $\psi ^{-1}_2(1-\overline{\delta })$ are also intervals. Then we can attain that, for $\forall t_1 \in \psi ^{-1}_1(\overline{\delta })$ and $\forall t_2 \in \psi ^{-1}_2(1-\overline{\delta })$,

$$\begin{aligned} f\left( t_1,t_2\right) \in \psi ^{-1}(\overline{\delta })=\psi ^{-1}(\delta ). \end{aligned}$$

For one thing, considering that f is increasing for $\zeta _1$ and decreasing for $\zeta _2$, it can be deduced that

$$\begin{aligned} \zeta _1\le t_1 \text{ and } \zeta _2\ge t_2 \Rightarrow f(\zeta _1, \zeta _2)\le f(t_1, t_2), \end{aligned}$$

which means that

$$\begin{aligned} \left\{ \zeta _1\le t_1\right\} \cap \left\{ \zeta _2\ge t_2\right\} \subseteq \left\{ f(\zeta _1, \zeta _2)\le f\left( t_1, t_2\right) \right\} . \end{aligned}$$

In accordance with the increase of the credibility measure $\mathrm{Cr}$, we can obtain

$$\begin{aligned} \mathrm{Cr}\left\{ \zeta \le f\left( t_1, t_2\right) \right\} \ge \mathrm{Cr}\left\{ \{\zeta _1\le t_1 \}\cap \{\zeta _2\ge t_2 \}\right\} . \end{aligned}$$

(21)

Then it can be attained that

$$\begin{aligned} \begin{array}{cl} &{} \mathrm{Cr}\left\{ \{\zeta _1\le t_1\}\cap \{\zeta _2\ge t_2\}\right\} \\ &{}=\mathrm{Cr}\left\{ \zeta _1\le t_1 \right\} \wedge \mathrm{Cr}\left\{ \zeta _2\ge t_2\right\} \\ &{}=\overline{\delta }\wedge \overline{\delta }=\overline{\delta }. \end{array} \end{aligned}$$

(22)

In accordance with Eqs. (21) and (22), we get

$$\begin{aligned} \mathrm{Cr}\left\{ \zeta \le f\left( t_1, t_2\right) \right\} \ge \overline{\delta }, \qquad \forall f\left( t_1, t_2\right) \in \psi ^{-1}(\delta ). \end{aligned}$$

(23)

For another thing, since f is increasing for $\zeta _1$ and decreasing for $\zeta _2$, it can be deduced that

$$\begin{aligned} f(\zeta _1, \zeta _2)\le f\left( t_1, t_2\right) \Rightarrow \zeta _1\le t_1 \text{ or } \zeta _2\ge t_2. \end{aligned}$$

(24)

Following from Eq. (24), we can get

$$\begin{aligned} \left\{ f(\zeta _1, \zeta _2)\le f(t_1, t_2)\right\} \subseteq \left\{ \zeta _1\le t_1\right\} \cup \left\{ \zeta _2\ge t_2\right\} . \end{aligned}$$

In terms of the increase of the credibility measure $\mathrm{Cr}$, it can be attained that

$$\begin{aligned} \mathrm{Cr}\left\{ \zeta \le f\left( t_1, t_2\right) \right\} \le \mathrm{Cr}\left\{ \{\zeta _1\le t_1 \right\} \cup \left\{ \zeta _2\ge t_2\}\right\} . \end{aligned}$$

(25)

Then it can be derived that

$$\begin{aligned} \begin{array}{cl} &{}\mathrm{Cr}\left\{ \{\zeta _1\le t_1\}\cup \{\zeta _2\ge t_2\}\right\} \\ &{}=\mathrm{Cr}\left\{ \zeta _1\le t_1 \right\} \vee \mathrm{Cr}\left\{ \zeta _2\ge t_2\right\} \\ &{}=\overline{\delta }\vee \overline{\delta }=\overline{\delta }. \end{array} \end{aligned}$$

(26)

In view of Eqs. (25) and (26), we have

$$\begin{aligned} \mathrm{Cr}\left\{ \zeta \le f\left( t_1, t_2\right) \right\} \le \overline{\delta }, \qquad \forall f\left( t_1, t_2\right) \in \psi ^{-1}(\delta ). \end{aligned}$$

(27)

Finally, combing Eqs. (23) and (27), we can get

$$\begin{aligned} \mathrm{Cr}\left\{ \zeta \le f_\delta \right\} =\overline{\delta }, \qquad \forall f\left( t_1, t_2\right) =f_\delta \in \psi ^{-1}(\delta ), \end{aligned}$$

where $\overline{\delta }=\sup \{\gamma \mid \psi ^{-1}(\gamma )=\psi ^{-1}(\delta )\}$ holds in accordance with Eq. (19). In terms of Definition 3, it can be known that $\psi ^{-1}(\delta )=f(\psi ^{-1}_1(\delta ), \psi ^{-1}_{2}$ $(1-\delta ))$ is just the ICD of $\zeta =f(\zeta _1,\zeta _2)$. $\square$

The proof of Theorem 6

Proof

Following from Definition 6, we can get that

$$\begin{aligned} \begin{array}{rl} E[\zeta ]&{}=\displaystyle \int _{0}^{+\infty }\mathrm{Cr}\{\zeta \ge t\} \mathrm{d}t-\int _{-\infty }^{0}\mathrm{Cr}\{\zeta \le t\} \mathrm{d}t\\ &{}=\displaystyle \int _{0}^{+\infty }\left( 1-\psi (t)\right) \mathrm{d}t-\int _{-\infty }^{0}\psi (t) \mathrm{d}t\\ &{}=\displaystyle \int _{0}^{+\infty } t \mathrm{d}\psi (t). \end{array} \end{aligned}$$

By taking $\delta$ to replace $\psi (t)$ and $\psi ^{-1}(\delta )$ to replace t, then it can be derived that

$$\begin{aligned} E[\zeta ]=\displaystyle \int _{0}^{1}\psi ^{-1}(\delta ) \mathrm{d}\delta . \square \end{aligned}$$

The proof of Theorem 8

Proof

In the light of Theorem 7, it is deduced that

$$\begin{aligned} \begin{array}{rl} E[f({\varvec{t}},{\varvec{\zeta }})]=&{}\displaystyle \int _{0}^{1}f({\varvec{t}},\psi ^{-1}_1(\delta ),\ldots ,\psi ^{-1}_k(\delta ), \psi ^{-1}_{k+1}\\ &{}(1-\delta ),\ldots ,\psi ^{-1}_n(1-\delta )) \mathrm{d}\delta . \end{array} \end{aligned}$$

In view of Theorem 5, the ICD of $h_v({\varvec{t}},\zeta _1,\zeta _2,\ldots ,$ $\zeta _n)$ is derived as

$$\begin{aligned} \begin{array}{rl} \phi ^{-1}_v(\delta )=&{}h_v({\varvec{t}},\psi _{1}^{-1}(\delta ),\ldots ,\psi _{k_{v}}^{-1}(\delta ),\psi _{k_{v}+1}^{-1}(1-\delta ),\\ &{}\ldots ,\psi _{n}^{-1}(1-\delta )). \end{array} \end{aligned}$$

It is not hard to find that $\mathrm{Cr}\{h_v({\varvec{t}},\zeta _1,\zeta _2,\ldots ,\zeta _n)$ $\le 0\}\ge \delta$ holds if and only if $\phi ^{-1}_v(\delta ) \le 0$. Especially, when $\phi ^{-1}_v(0.5)$ is not unique, $\mathrm{Cr}\{h_v({\varvec{t}},\zeta _1,\zeta _2,$ $\ldots ,\zeta _n)\le 0\}\ge 0.5$ holds if only and if $\inf \phi ^{-1}_v(0.5)$ $\le 0$. $\square$