Abstract
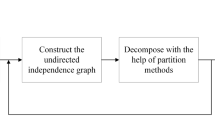
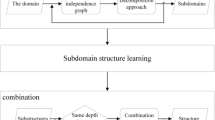
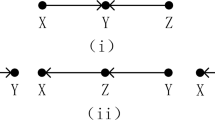
The decomposition structure learning algorithm is the most effective for the structure learning of large Bayesian networks. Maximal prime subgraph decomposition is one of the main methods of Bayesian network structure decomposition learning. The key to maximal prime subgraph decomposition is the search for separators. However, existing methods of searching separators are inefficient, because they all search for separators globally. To improve the accuracy and speed of Bayesian network structure decomposition learning algorithm, we design an efficient recursive Bayesian network structure decomposition learning algorithm (ERDA) and propose a method to locally search for separators recursively for ERDA in this paper. Each iteration includes two steps. The first stage is to determine a target node according to the minimum node degree. The second stage is to perform a local search for the separator in the adjacent node set of the target node. The separator splits the network into two subgraphs, where the small subgraph contains the target node and the larger one does not. Local search is only performed iteratively in the large subgraph. Finally, we conduct experiments on various samples to compare the Hamming distance and running time of ERDA method with four existing methods and ERDA method based on recursive local search for separators with ERDA based on global search for separators. Then, we apply our method to the German credit dataset, which is a real data from UCI, to obtain its credit causality model. All the algorithms are compiled and implemented in MATLAB. Experiments show that our method has better performance than state-of-the-art methods and has applicability to real problems.







Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
Enquiries about data availability should be directed to the authors.
References
Aliferis CF, Statnikov AR, Tsamardinos I, Mani S, Koutsoukos XD (2010) Local causal and markov blanket induction for causal discovery and feature selection for classification part I: algorithms and empirical evaluation. J Mach Learn Res 11:171–234. https://doi.org/10.1145/1756006.1756013
Berry A, Pogorelcnik R, Simonet G (2010) an introduction to clique minimal separator decomposition. Algorithms 3:197–215. https://doi.org/10.3390/a3020197
Chatrabgoun O, Hosseinian-Far A, Chang V, Stocks NG, Daneshkhah A (2018) Approximating non-Gaussian Bayesian networks using minimum information vine model with applications in financial modelling. J Comput Sci 24:266–276. https://doi.org/10.1016/j.jocs.2017.09.002
Cheng J, Greiner R, Kelly J, Bell D, Liu WR (2002) Learning Bayesian networks from data: An information-theory based approach. Artif Intell 137:43–90. https://doi.org/10.1016/S0004-3702(02)00191-1
Chickering DM, Heckerman D, Mee C (2004) Large-sample learning of Bayesian networks is NP-hard. J Mach Learn Res 5:1287–1330. https://doi.org/10.48550/arXiv.1212.2468
Contaldi C, Vafaee F, Nelson PC (2019) Bayesian network hybrid learning using an elite-guided genetic algorithm. Artif Intell Rev 52:245–272. https://doi.org/10.1007/s10462-018-9615-5
Cooper GF, Herskovits E (1992) A Bayesian method for the induction of probabilistic networks from data. Mach Learn 9:309–347. https://doi.org/10.1023/A:1022649401552
Dai JG, Ren J, Du WC (2020) Decomposition-based Bayesian network structure learning algorithm using local topology information. Knowl-Based Syst. https://doi.org/10.1016/j.knosys.2020.105602
Di De Lez V, Pigeot I (2001) Judea Pearl: Causality: Models, reasoning, and inference. Politische Vierteljahresschrift 42:313–315. https://doi.org/10.1007/s11615-001-0048-3
Freeman LC (1977) A Set of Measures of Centrality Based on Betweenness. Sociometry 40:35–41. https://doi.org/10.2307/3033543
Heckerman D (1995) Learning Bayesian networks: the combination of knowledge and statistical data. Mach Learn. https://doi.org/10.1007/BF00994016
Lauritzen SL (1996) Graphical models. Oxford, Clarendon Press
Lauritzen SL, Dawid AP, Larsen BN, Leimer H-G (1990) Independence properties of directed Markov fields. Networks 20:491–505. https://doi.org/10.1002/net.3230200503
Li Y, Yang Y, Wang W, Yang W (2015) An algorithm for learning the skeleton of large Bayesian network. Int J Artif Intell Tools. https://doi.org/10.1142/s0218213015500128
Liu H, Zhou S, Lam W, Guan J (2017) A new hybrid method for learning bayesian networks: separation and reunion. Knowl-Based Syst 121:185–197. https://doi.org/10.1016/j.knosys.2017.01.029
Liu K, Cui YN, Ren J, Li PR (2021) An improved particle swarm optimization algorithm for Bayesian network structure learning via local information constraint. IEEE Access 9:40963–40971. https://doi.org/10.1109/ACCESS.2021.3065532
Mihaljević B, Bielza C, Larrañaga P (2021) Bayesian networks for interpretable machine learning and optimization. Neurocomputing 456:648–665. https://doi.org/10.1016/j.neucom.2021.01.138
Neil M, Fenton N, Osman M, McLachlan S (2020) Bayesian network analysis of Covid-19 data reveals higher infection prevalence rates and lower fatality rates than widely reported. J Risk Res. https://doi.org/10.1101/2020.05.25.20112466
Olesen GK, Madsen AL (2002) Maximal prime subgraph decomposition of Bayesian networks. IEEE Trans Syst Man Cybern Part B. https://doi.org/10.1109/3477979956
Pan H, Yang X (2021) Intelligent recommendation method integrating knowledge graph and Bayesian network. Soft Comput. https://doi.org/10.1007/s00500-021-05735-z
Schwarz G (1978) Estimating the dimension of a model. Ann Stat 6(461–64):4. https://doi.org/10.1214/aos/1176344136
Spirtes P, Glymour C (2016) An algorithm for fast recovery of sparse causal graphs. Soc Sci Comput Rev 9:62–72. https://doi.org/10.1177/089443939100900106
Tabar VR, Eskandari F, Salimi S, Zareifard H (2018) Finding a set of candidate parents using dependency criterion for the K2 algorithm. Pattern Recogn Lett 111:23–29. https://doi.org/10.1016/j.patrec.2018.04.019
Tsamardinos I, Brown LE, Aliferis CF (2006) The max-min hill-climbing Bayesian network structure learning algorithm. Mach Learn 65:31–78. https://doi.org/10.1007/s10994-006-6889-7
Varshney D, Kumar S, Gupta V (2017) Predicting information diffusion probabilities in social networks: a Bayesian networks based approach. Knowl-Based Syst 133:66–76. https://doi.org/10.1016/j.knosys.2017.07.003
Xie X, Zhi G (2008) A recursive method for structural learning of directed acyclic graphs. J Mach Learn Res 9:459–483. https://doi.org/10.1145/1390681.1390695
Xie X, Geng Z, Zhao Q (2006) Decomposition of structural learning about directed acyclic graphs. Artif Intell 170:422–439. https://doi.org/10.1016/j.artint.2005.12.004
Yan C, Zhou S (2020) Effective and scalable causal partitioning based on low-order conditional independent tests. Neurocomputing 389:146–154. https://doi.org/10.1016/j.neucom.2020.01.021
Yang XL, Wang YJ, Ou Y, Tong YH (2019) Three-fast-inter incremental association Markov blanket learning algorithm. Pattern Recogn Lett 122:73–78. https://doi.org/10.1016/j.patrec.2019.02.002
Zeng Y, Hernandez JC (2008) A decomposition algorithm for learning Bayesian network structures from data. Adv Knowl Discov Data Min. https://doi.org/10.1007/978-3-540-68125-0_39
Zhang X, Mahadevan S (2021) Bayesian network modeling of accident investigation reports for aviation safety assessment. Reliab Eng Syst Saf. https://doi.org/10.1016/j.ress.2020.107371
Zhang X, Xue Y, Xingyang Lu, Jia S (2018) Differential-evolution-based coevolution ant colony optimization algorithm for Bayesian network structure learning. Algorithms. https://doi.org/10.3390/a11110188
Zhu M, Liu S (2012) A decomposition algorithm for learning Bayesian networks based on scoring function. J Appl Math 2012:1–17. https://doi.org/10.1155/2012/974063
Funding
This study was supported by Natural Science Foundation of China (No. 61973067).
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Xiaolong Jia, Hongru Li and Huiping Guo. The first draft of the manuscript was written by Xiaolong Jia and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
All the authors of this research paper declare that there is no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Jia, X., Li, H. & Guo, H. A recursive local search method of separators for Bayesian network decomposition structure learning algorithm. Soft Comput 27, 3673–3687 (2023). https://doi.org/10.1007/s00500-022-07647-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-022-07647-y