Skip to main content
SpringerLink
Log in

A Lagrange spectral collocation method for weakly singular fuzzy fractional Volterra integro-differential equations

  • Fuzzy systems and their mathematics
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

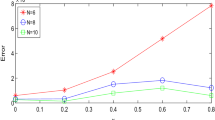
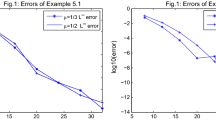
A linear fractional-order weakly singular fuzzy Volterra integro-differential equation has been examined. In this case, the Caputo fractional-order derivative has been considered. A new type of spectral collocation method based on the Lagrange interpolation basis polynomial has been studied and modified for the equation. In the spectral collocation technique, it is necessary to choose collocation points to find the numerical solution of the equation. We have chosen the collocation points based on the Chebyshev extreme points or Gauss–Lobatto–Chebyshev points of order N. We have used the fractional Gauss–Jacobi quadrature method to approximate the fractional integral terms of the proposed equation. Also, the integral operators have been approximated by the Gauss quadrature rule. A theorem has been given to demonstrate that there exists a unique solution for the proposed equation. In addition, Banach’s fixed point principle has been applied in the proof of the existence and uniqueness theorem. The convergence analysis of the proposed numerical technique is given in the form of some lemmas and theorems. Some numerical experiments have been performed to verify the proposed method. Five different kinds of errors have been computed and compared to do the error analysis. Also, these kinds of error analysis have been examined by analyzing the result in the form of different graphs and tables. The numerical results of the proposed technique have been compared with an existing method, Adomian decomposition method (ADM).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Data availability

Enquiries about data availability should be directed to the authors.

References

  • Abbasbandy S, Hashemi MS, Hashim I (2013) On convergence of homotopy analysis method and its application to fractional integro-differential equations. Quaest Math 36(1):93–105

    Article  MathSciNet  MATH  Google Scholar 

  • Agarwal RP, Lakshmikantham V, Nieto JJ (2010) On the concept of solution for fractional differential equations with uncertainty. Nonlinear Anal Theory Methods Appl 72(6):2859–2862

    Article  MathSciNet  MATH  Google Scholar 

  • Alijani Z, Kangro U (2022) Numerical solution of a linear fuzzy Volterra integral equation of the second kind with weakly singular kernels. Soft Comput 26(22):12009–12022

    Article  Google Scholar 

  • Alijani Z, Baleanu D, Shiri B, Wu GC (2020) Spline collocation methods for systems of fuzzy fractional differential equations. Chaos Solitons Fractals 131:109510

    Article  MathSciNet  MATH  Google Scholar 

  • Alijani Z, Kangro U (2021) On the smoothness of the solution of fuzzy Volterra integral equations of the second kind with weakly singular kernels. Numer Funct Anal Optim 1–15

  • Allahviranloo T, Armand A, Gouyandeh Z (2014) Fuzzy fractional differential equations under generalized fuzzy Caputo derivative. J Intell Fuzzy Syst 26(3):1481–1490

    Article  MathSciNet  MATH  Google Scholar 

  • Arikoglu A, Ozkol I (2009) Solution of fractional integro-differential equations by using fractional differential transform method. Chaos Solitons Fractals 40(2):521–529

    Article  MathSciNet  MATH  Google Scholar 

  • Bica AM, Ziari S, Satmari Z (2022) An iterative method for solving linear fuzzy fractional integral equation. Soft Comput 1–12

  • Bica AM, Popescu C (2014) Approximating the solution of nonlinear Hammerstein fuzzy integral equations. Fuzzy Sets Syst 245:1–17

    Article  MathSciNet  MATH  Google Scholar 

  • Bidari A, Dastmalchi Saei F, Baghmisheh M, Allahviranloo T (2021) A new Jacobi tau method for fuzzy fractional Fredholm nonlinear integro-differential equations. Soft Comput 25(8):5855–5865

    Article  MATH  Google Scholar 

  • Biswas S, Roy TK (2019) A semianalytical method for fuzzy integro-differential equations under generalized Seikkala derivative. Soft Comput 23(17):7959–7975

    Article  MATH  Google Scholar 

  • Biswas S, Moi S, Sarkar SP (2021) Numerical solution of fuzzy Fredholm integro-differential equations by polynomial collocation method. Comput Appl Math 40(7):1–33

    Article  MathSciNet  MATH  Google Scholar 

  • Canuto C, Hussaini MY, Quarteroni A, Zang TA (2007) Spectral methods: fundamentals in single domains. Springer, Berlin

    Book  MATH  Google Scholar 

  • Congxin W, Gong Z (2001) On Henstock integral of fuzzy-number-valued functions (i). Fuzzy Sets Syst 120(3):523–532

    Article  MathSciNet  MATH  Google Scholar 

  • Diethelm K (2020) The analysis of fractional differential equations, volume 2004 of lecture notes in mathematics. Springer, Berlin

    Google Scholar 

  • Diethelm K, Ford NJ (2002) Analysis of fractional differential equations. J Math Anal Appl 265(2):229–248

    Article  MathSciNet  MATH  Google Scholar 

  • Ho V, Van Hoa N (2019) Uncertain fractional differential equations on a time scale under granular differentiability concept. Comput Appl Math 38(3):1–22

    MathSciNet  MATH  Google Scholar 

  • Ho V, Van Hoa N (2020) Applications of contractive-like mapping principles to fuzzy fractional integral equations with the kernel \(\psi \)-functions. Soft Comput 24(24):18841–18855

    Article  MATH  Google Scholar 

  • Jahanshahi S, Babolian E, Torres DF, Vahidi AR (2017) A fractional Gauss-Jacobi quadrature rule for approximating fractional integrals and derivatives. Chaos Solitons Fractals 102:295–304

    Article  MathSciNet  MATH  Google Scholar 

  • Kumar S, Nieto JJ, Ahmad B (2022) Chebyshev spectral method for solving fuzzy fractional Fredholm-Volterra integro-differential equation. Math Comput Simul 192:501–513

    Article  MathSciNet  MATH  Google Scholar 

  • Lepik Ü (2009) Solving fractional integral equations by the Haar wavelet method. Appl Math Comput 214(2):468–478

    MathSciNet  MATH  Google Scholar 

  • Li Z-B, He J-H (2010) Fractional complex transform for fractional differential equations. Math Comput Appl 15(5):970–973

    MathSciNet  MATH  Google Scholar 

  • Mazandarani M, Kamyad AV (2013) Modified fractional Euler method for solving fuzzy fractional initial value problem. Commun Nonlinear Sci Numer Simul 18(1):12–21

    Article  MathSciNet  MATH  Google Scholar 

  • Mizukoshi MT, Barros LD, Chalco-Cano Y, Roman-Flores H, Bassanezi RC (2007) Fuzzy differential equations and the extension principle. Inf Sci 177(17):3627–3635

    Article  MathSciNet  MATH  Google Scholar 

  • Moi S, Biswas S, Sarkar SP (2022) A new collocation method for fuzzy singular integro-differential equations. Int J Appl Comput Math 8(2):1–33

    Article  MathSciNet  Google Scholar 

  • Najafi N, Allahviranloo T (2020) Combining fractional differential transform method and reproducing kernel Hilbert space method to solve fuzzy impulsive fractional differential equations. Comput Appl Math 39(2):1–25

    Article  MathSciNet  MATH  Google Scholar 

  • Oldham KB, Spanier J (1974) The fractional calculus. Academic Press, New York

    MATH  Google Scholar 

  • Padmapriya V, Kaliyappan M, Parthiban V (2017) Solution of fuzzy fractional integro-differential equations using a domian decomposition method. J Inform Math Sci 9(3):501–507

    Google Scholar 

  • Panda SK, Abdeljawad T, Ravichandran C (2020) Novel fixed point approach to Atangana-Baleanu fractional and lp-Fredholm integral equations. Alex Eng J 59(4):1959–1970

  • Pandey P, Singh J (2022) An efficient computational approach for nonlinear variable order fuzzy fractional partial differential equations. Comput Appl Math 41(1):1–21

    Article  MathSciNet  MATH  Google Scholar 

  • Podlubny I (1999) Fractional differential equations, mathematics in science and engineering. Academic Press, New York

    MATH  Google Scholar 

  • Ragozin DL (1970) Polynomial approximation on compact manifolds and homogeneous spaces. Trans Am Math Soc 150(1):41–53

    Article  MathSciNet  MATH  Google Scholar 

  • Sabzi K, Allahviranloo T, Abbasbandy S (2020) A fuzzy generalized power series method under generalized Hukuhara differentiability for solving fuzzy Legendre differential equation. Soft Comput 24(12):8763–8779

    Article  MATH  Google Scholar 

  • Seifi A, Lotfi T, Allahviranloo T (2019) A new efficient method using Fibonacci polynomials for solving of first-order fuzzy Fredholm-Volterra Integro-differential equations. Soft Comput 23(19):9777–9791

    Article  MATH  Google Scholar 

  • Sevinik-Adıgüzel R, Aksoy Ü, Karapınar E, Erhan IM (2021) Uniqueness of solution for higher-order nonlinear fractional differential equations with multi-point and integral boundary conditions. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas 115(3):1–16

  • Usta F (2021) Numerical analysis of fractional Volterra integral equations via Bernstein approximation method. J Comput Appl Math 384:113198

    Article  MathSciNet  MATH  Google Scholar 

  • Wang X, Luo D, Zhu Q (2022) Ulam-hyers stability of caputo type fuzzy fractional differential equations with time-delays. Chaos Solitons Fractals 156:111822

    Article  MathSciNet  MATH  Google Scholar 

  • Zhendong G (2019) Spectral collocation method for weakly singular Volterra integro-differential equations. Appl Numer Math 143:263–275

    Article  MathSciNet  MATH  Google Scholar 

  • Zhendong G, Chen Y (2014) Chebyshev spectral-collocation method for a class of weakly singular Volterra integral equations with proportional delay. J Numer Math 22(4):311–342

    MathSciNet  MATH  Google Scholar 

  • Ziari S, Allahviranloo T, Pedrycz W (2021) An improved numerical iterative method for solving nonlinear fuzzy Fredholm integral equations via Picard’s method and generalized quadrature rule. Comput Appl Math 40(6):1–22

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

For the financial assistance of this research work, Sandip Moi thanks the Council of Scientific and Industrial Research (CSIR), Government of India (File No.- 08/003(0135)/2019-EMR-I).

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Engineering Science and Technology, Shibpur, B. Garden, Howrah, 711103, India

    Sandip Moi & Smita Pal Sarkar

  2. Discipline of Mathematics, School of Sciences, Indira Gandhi National Open University, New Delhi, 110068, India

    Suvankar Biswas

Authors
  1. Sandip Moi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Suvankar Biswas
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Smita Pal Sarkar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Suvankar Biswas.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Moi, S., Biswas, S. & Sarkar, S.P. A Lagrange spectral collocation method for weakly singular fuzzy fractional Volterra integro-differential equations. Soft Comput 27, 4483–4499 (2023). https://doi.org/10.1007/s00500-023-07829-2

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-023-07829-2

Keywords

Search

Navigation