Abstract
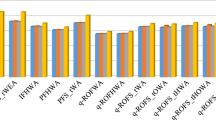
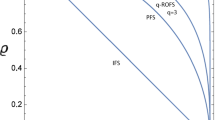
The desideratum behind this article is to study some primary perceptions of q-rung orthopair fuzzy soft (q-ROFS) ring of sets, q-rung orthopair fuzzy soft \(\sigma \)-algebra (q-ROFS \(\sigma \)-algebra) and q-rung orthopair fuzzy soft measure (q-ROFS measure). Some characteristics and their related results of these notions are introduced. The notions of q-ROFS \(\sigma \)-algebra and q-ROFSM are the extensions of crisp \(\sigma \)-algebra and crisp measure, respectively. Also, a multi-criteria group decision-making (MCGDM) method based on q-rung orthopair fuzzy soft sets (q-ROFSSs), mean proportional operator and newly proposed score function is proposed. Furthermore, an application of the proposed methodology toward a clean environment is given to handle uncertainties and vagueness.


Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
Enquiries about data availability may be directed to the authors.
References
Ali MI (2018) Another view on \(q\)-rung orthopair fuzzy sets. Int J Intell Syst 33:2139–2153
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Elshaboury N, Marzouk M (2022) Prioritizing water distribution pipelines rehabilitation using machine learning algorithms. Soft Comput 26(5):5179–5193
Feng F, Zhang C, Akram M, Zhang J (2022) Multiple attribute decision making based on probabilistic generalized orthopair fuzzy sets. Granul Comput. https://doi.org/10.1007/s41066-022-00358-7
Goker N (2021) A novel integrated intuitionistic fuzzy decision aid for agile outsourcing provider selection: a COVID-19 pandemic-based scenario analysis. Soft Comput 25:13723–13740. https://doi.org/10.1007/s00500-021-06037-0
Halton JH (2008) Sigma algebra theorems. Monte Carlo Methods Appl 14(2):171–189
Hamid MT, Riaz M, Afzal D (2020) Novel MCGDM with q-rung orthopair fuzzy soft sets and TOPSIS approach under q-rung orthopair fuzzy soft topology. J Intell Fuzzy Syst 39(3):3853–3871
Hamid MT, Riaz M, Naeem K (2022) q-Rung orthopair fuzzy soft topology with multi-attribute decision-making. In: Garg H (ed) q-Rung orthopair fuzzy sets. Springer, Singapore. https://doi.org/10.1007/978-981-19-1449-2_2
Khameneh AZ, Kilicman A (2013) On soft \(\sigma \)-algebras. Malays J Math Sci 7(1):17–29
Kumari PN, Kumar DVSRA (2018) Soft sets and sigma algebras. Int J Math Trends Technol 55(1):10–13
Mahmood T, Ali Z (2022) Analysis of Maclaurin symmetric mean operators for managing complex interval-valued q-rung orthopair fuzzy setting and their applications. J Comput Cognit Eng 2:98–115. https://doi.org/10.47852/bonviewJCCE2202164
Molodtsov D (1999) Soft set theory-first results. Comput Math Appl 37:19–31
Mukherjee A, Saha A, Das AK (2015) Measurable soft sets. Int J Open Probl Comput Sci Math 8(4):1–14
Naeem K (2017) Soft set theory & soft sigma algebras. LAP LAMBERT Academic Publishing, London, pp 1–116
Naeem K, Memiş S (2022) Picture fuzzy soft \(\sigma \)-algebra and picture fuzzy soft measure and their applications to multi-criteria decision-making. Granul Comput. https://doi.org/10.1007/s41066-022-00333-2
Naeem K, Riaz M, Afzal D (2020) Fuzzy neutrosophic soft \(\sigma \)-algebra and fuzzy neutrosophic soft measure with applications. J Intell Fuzzy Syst 39(1):277–287
Peng X, Liu L (2019) Information measures for q-rung orthopair fuzzy sets. Int J Intell Syst 34(8):1795–1834
Pinar A, Daneshvar RB, Ozdemir YS (2021) q-Rung orthopair fuzzy TOPSIS method for green supplier selection problem. Sustainability 13(2):985. https://doi.org/10.3390/su13020985
Raghunathan K, Gowtham Y, Ahmed I, Ravichandran KS, Kar S (2020) Solving green supplier selection problem using q-rung orthopair fuzzy-based decision framework with unknown weight information. Appl Soft Comput 94:106431. https://doi.org/10.1016/j.asoc.2020.106431
Riaz M, Naeem K (2016) Measurable soft mappings. Punjab Univ J Math 48(2):19–34
Sarkar A, Biswas A, Kundu M (2022) Development of q-rung orthopair trapezoidal fuzzy Einstein aggregation operators and their application in MCGDM problems. J Comput Cognit Eng 1(3):109–121. https://doi.org/10.47852/bonviewJCCE2202162
Wan B, Hu Z, Garg H, Cheng Y, Han M (2023) An integrated group decision-making method for the evaluation of hypertension follow-up systems using interval-valued q-rung orthopair fuzzy sets. Complex Intell Syst. https://doi.org/10.1007/s40747-022-00953-w
Wei G, Wei C, Guo Y (2021) EDAS method for probabilistic linguistic multiple attribute group decision making and their application to green supplier selection. Soft Comput 25:9045–9053. https://doi.org/10.1007/s00500-021-05842-x
Yager RR (2013) Pythagorean fuzzy subsets. In: 2013 joint IFSA World Congress and NAFIPS annual meeting (IFSA/NAFIPS), Edmonton, Canada, IEEE 2013, pp 57–61
Yager RR (2014) Pythagorean membership grades in multi-criteria decision making. IEEE Trans Fuzzy Syst 22(4):958–965
Yager RR (2017) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1220–1230
Yu Q, Cao J, Tan L et al (2022) Multiple attribute decision-making based on Maclaurin symmetric mean operators on q-rung orthopair cubic fuzzy sets. Soft Comput 26:9953–9977. https://doi.org/10.1007/s00500-022-07363-7
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Zhang H, Nan T, He Y (2022) q-Rung orthopair fuzzy N-soft aggregation operators and corresponding applications to multiple-attribute group decision making. Soft Comput 26:6087–6099. https://doi.org/10.1007/s00500-022-07126-4
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Contributions
The authors contributed to each part of this paper equally. The authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Hamid, M.T., Naeem, K. & Karaaslan, F. A futuristic conception about q-rung orthopair fuzzy soft measure with application to guarantee the clean environment for healthy life. Soft Comput 27, 11931–11939 (2023). https://doi.org/10.1007/s00500-023-08724-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-023-08724-6