Abstract
This paper presents an important method for the algebraic synthesis of the winding layout of AC machines. It applies in general to integral-slot and fractional-slot windings, including non-overlapping windings, so it can be claimed to unify the synthesis task. Moreover, it results in the highest possible winding factor at the working harmonic. A harmonic content analysis is presented, including the calculation of the winding factor by the closed-form expression of Klíma for several examples, which also applies in general to the entirety of this class of windings. Exact agreement with the calculation based on the DFT corroborates the results.
Zusammenfassung
In diesem Beitrag wird eine Methode für die algebraische Wicklungsauslegung von Drehfeldmaschinen vorgestellt. Die Systematik ist gültig für symmetrische Ganzloch- und Bruchlochwicklungen mit verteilten sowie geometrisch konzentrierten Spulen und vereinheitlicht die Syntheseaufgabe. Darüber hinaus führt es zum höchstmöglichen Wicklungsfaktor der Arbeitswelle. Eine Analysemethodik des Oberwellengehalts wird vorgestellt, die die Berechnung der Wicklungsfaktoren durch den geschlossenen Ausdruck von Klíma einschließt, der allgemein für die Gesamtheit dieser Klasse von Wicklungen gilt. Die Untersuchung schließt mit der Anwendung des Ansatzes auf mehrere Beispiele. Eine exakte Übereinstimmung mit der Berechnung auf Basis der DFT untermauert die Ergebnisse.



Similar content being viewed by others
Abbreviations
- \(Q\) :
-
Number of stator slots
- \(p\) :
-
Number of pole pairs
- \(\mathrm{{b}}\) :
-
Subscript: basic winding
- \(k_{\mathrm{{w}}}\) :
-
Winding factor
- \(k_{\mathrm{{d}}}\) :
-
Distribution (breadth) factor
- \(k_{\mathrm{{p}}}\) :
-
Pitch (chording) factor
- \(m\) :
-
Number of phases
- \(n_{\mathrm{{l}}}\) :
-
Number of layers
- \(T_{\mathrm{{ph}}}\) :
-
Series turns per phase
- \(I_{\mathrm{{c}}}\) :
-
Coil current
- \(T_{\mathrm{{c}}}\) :
-
Coil turns
- \(q\) :
-
Slots per pole and phase, \(q =\frac{Q}{m2p}\)
-
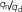 :
: -
Reduced numerator/denominator of \(q\)
- \(q_{1}\) :
-
Slot number assigned to positive phase belts
- \(q_{2}\) :
-
Slot number assigned to negative phase belts
- \(t\) :
-
Winding symmetry factor
- \(y_{\mathrm{{p}}}\) :
-
Theoretical coil pitch
- \(y_{\mathrm{{d}}}\) :
-
Implemented coil pitch
- \(Y_{\mathrm{{k}}}\) :
-
Fictitious commutator pitch
- \(\nu \) :
-
Harmonic order
- \(\text{gcd}\) :
-
Greatest common divisor
- \(\text{SC}\) :
-
Enhanced symmetrical component
References
Alberti, L., Bianchi, N. (2013): Theory and design of fractional-slot multilayer windings. IEEE Trans. Ind. Appl., 49(2), 841–849.
Arnold, E. (1912): Die Wicklungen der Wechselstrommaschinen [AC machine windings]. Berlin: Springer.
Brune, K., Seinsch, H., Steinbrink, J. (2003): Conducted emission of synchronous generators and its dependence on design features. Electr. Eng., 85, 71–81.
Cros, J., Viarouge, P. (2002): Synthesis of high performance PM motors with concentrated windings. IEEE Trans. Energy Convers., 17(2), 248–253.
EL-Refaie, A. M. (2010): Fractional-slot concentrated-windings synchronous permanent magnet machines: opportunities and challenges. IEEE Trans. Ind. Electron., 57(1), 107–121.
Fitzgerald, A., Kingsly, C., Umans, S. D. (1990): Electric machinery. New York: McGraw-Hill.
Kauders, W. (1932): Systematik der Drehstromwicklungen [Systematics of three-phase windings]. Elektrotech. Masch.bau, 50(6), 88–94. 106–108.
Kauders, W. (1934): Systematik der Drehstromwicklungen [Systematics of three-phase windings]. Elektrotech. Masch.bau, 52(7), 85–92.
Klíma, V. (1979): On the theorem of the sum of squares of winding factors invariance. Acta Tech. CSAV, 24(3), 365–388.
Kremser, A. (1988): Theorie der mehrsträngigen Bruchlochwicklungen und Berechnung der Zweigströme in Drehfeldmaschinen [Theory of multi-phase fractional slot windings and the calculation of the branch currents in rotating field machines]. Ph.D. thesis, University of Hanover.
Lipo, T., Liu, W. (2020): Comparison of AC motors to an ideal machine part I – conventional AC machines. IEEE Trans. Ind. Appl., 56(2), 1346–1355.
Lipo, T., Liu, W., Du, Z. (2020): Comparison of AC motors to an ideal machine part II – non-sinusoidal AC machines. IEEE Trans. Ind. Appl., 56(2), 4727–4737.
Liwschitz, M. M. (1943): Distribution factors and pitch factors of the harmonics of a fractional-slot winding. Trans. Am. Inst. Electr. Eng., 62(10), 664–666.
Meier, F., Meier, S., Soulard, J. (2008): Emetor - an educational web-based design tool for permanent-magnet synchronous machines. In Proceedings of the 2008 international conference on electrical machines.
Scuiller, F. (2020): General, compact and easy-to-compute winding factor formulation. IET Electr. Power Appl., 14(8), 1430–1437.
Seinsch, H. O. (1992): Oberfelderscheinungen in Drehfeldmaschinen: Grundlagen zur analytischen und numerischen Berechnung [Spatial harmonics phenomena in AC machines]. Leipzig: Teubner.
Soulard, J., Meier, F. (2011): Design guidelines and models for PMSMs with non-overlapping concentrated windings. Compel, 30(1), 72–83.
Stipetic, S., Zarko, D., Popescu, M. (2015): Scaling laws for synchronous permanent magnet machines. In Tenth international conference on ecological vehicles and renewable energies.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Germishuizen, J., Steckel, R. & Kremser, A. Algebraic synthesis and analysis of windings for AC machines. Elektrotech. Inftech. 138, 78–84 (2021). https://doi.org/10.1007/s00502-021-00873-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00502-021-00873-6


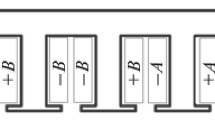
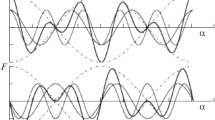
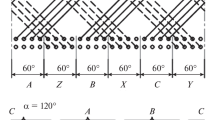
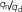 :
: