Skip to main content

Advertisement

Springer Nature Link
Log in

Improved hybrid wavelet neural network methodology for time-varying behavior prediction of engineering structures

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

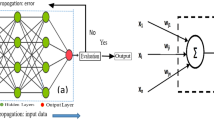
An improved neuro-wavelet modeling (NWM) methodology is presented, and it aims at improving prediction precision of time-varying behavior of engineering structures. The proposed methodology distinguishes from the existing NWM methodology by featuring the distinctive capabilities of constructing optimally uncoupled dynamic subsystems in light of the redundant Haar wavelet transform (RHWT) and optimizing neural network. In particular, two techniques of imitating wavelet packet transform of RHWT and reconstructing the major crests of power spectrum of analyzed data are developed with the aim of constructing the optimally uncoupled dynamic subsystems from time-varying data. The resulting uncoupled dynamic subsystems make the underlying dynamic law of time-varying behavior more tractable than the raw scale subwaves arose from the RHWT, and they provide a platform for multiscale modeling via individual modeling at the uncoupled dynamic subsystem level. Furthermore, on each uncoupled dynamic subsystem, the technique of optimal brain surgeon in conjunction with a new dynamic mechanism refreshing is employed to optimize the neural network, and the recombination of the modeling outcomes on every subsystem constitutes the overall modeling of time-varying behavior. The improved NMW methodology offers a feasible framework of multiscale modeling due to its flexibility, adaptability and rationality, and it is particularly useful for prediction applications of time-varying behavior of engineering structures. As an illustrative example, the improved NWM methodology is applied to model and forecast dam deformation, and the results show that the methodology possesses positive advantages over the existing multiscale and single scale modeling techniques. The improved NMW methodology is promising and valuable for the safety monitoring and extreme event warning of engineering structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Dascal O (1987) Postconstruction deformations of rockfill dams. J Geotech Eng Div 113(1):46–59. doi:10.1061/(ASCE)0733-9410(1987)113:1(46)

    Article  Google Scholar 

  2. Habibagahi G (2002) Post-construction settlement of rockfill dams analyzed via adaptive network-based fuzzy inference systems. Comput Geotech 29(3):211–233. doi:10.1016/S0266-352X(01)00025-8

    Article  Google Scholar 

  3. Touileb BN, Bonnelli S, Anthiniac P, Carrere A, Debordes D, La Barbera G, Bani A, Mazza G (2000) Settlement by wetting of the upstream rockfills of large dams. In: Proceedings of the 53rd Canadian geotechnical conference, Montreal, vol 1, pp 263–270

  4. Szostak-Chrzanowski A, Chrzanowski A, Massiera M (2005) Use of deformation monitoring results in solving geomechanical problems––case studies. Eng Geol 79(1–2):3–12. doi:10.1016/j.enggeo.2004.10.014

    Article  Google Scholar 

  5. Trifunac MD, Hudson DE (1971) Analysis of the Pacoima dam accelerogram—San Fernando, California, earthquake of 1971. Bull Seismol Soc Am 61(5):1393–1411

    Google Scholar 

  6. Wu WM, Wang SS (2007) One-dimensional modeling of dam-break flow over movable beds. J Hydraul Eng 133(1):48–58. doi:10.1061/(ASCE)0733-9429(2007)133:1(48)

    Article  Google Scholar 

  7. Bayrak T (2007) Modeling the relationship between water level and vertical displacements on the Yamula Dam, Turkey. Nat Hazards Earth Syst Sci 7(2):289–297

    Article  Google Scholar 

  8. Hudnut K, Behr J (1998) Continuous GPS monitoring of structural deformation at Pacoima dam, California. Seismol Res Lett 69(4):299–308

    Google Scholar 

  9. ICOLD (1988) World registers of dams. International Commission on Large Dams, Paris

  10. Szostak-Chrzanowski A, Massiéra M, Chrzanowski A, Le Hoan F, Whitaker C (2002) Verification of material parameters of earthen dams at diamond valley lake using geodetic measurements. In: Proceedings of the XXII FIG international congress, Washington

  11. Pytharouli SI, Stiros SC (2005) Ladon dam (Greece) deformation and reservoir level fluctuations, evidence for a causative relationship from the spectral analysis of a geodetic monitoring record. Eng Struct 27(3):361–370. doi:10.1016/j.engstruct.2004.10.012

    Article  Google Scholar 

  12. De Sortisa A, Paoliani P (2007) Statistical analysis and structural identification in concrete dam monitoring. Eng Struct 29(1):110–120. doi:10.1016/j.engstruct.2006.04.022

    Article  Google Scholar 

  13. Hudnut K (1996) Continuous GPS monitoring of dam deformation. Eos Trans AGU 77(46):F139

    Google Scholar 

  14. Wu ZR, Su HZ (2005) Dam health diagnosis and evaluation. Smart Mater Struct 14:S130–S136. doi:10.1088/0964-1726/14/3/016

    Article  Google Scholar 

  15. ICOLD (2000) Bulletin 118, automated dam monitoring systems––guidelines and case histories. International Commission on Large Dams, Paris

  16. Cao ZX, Pender G, Wallis S, Carling P (2004) Computational dam-break hydraulics over erodible sediment bed. J Hydraul Eng 130(7):689–703. doi:10.1061/(ASCE)0733-9429(2004)130:7(689)

    Article  Google Scholar 

  17. Barnaba C, Priolo1 E, Vuan1 A, Romanelli M (2007) Site effect of the strong-motion site at Tolmezzo-Ambiesta dam in northeastern Italy. Bull Seismol Soc Am 97(1B):339–346

    Google Scholar 

  18. Fedele R, Maier G, Miller B (2006) Health assessment of concrete dams by overall inverse analyses and neural networks. Int J Fract 137(1–4):151–172. doi:10.1007/s10704-006-6582-7

    Article  Google Scholar 

  19. Tayfur G, Swiatek D, Wita A, Singh VP (2005) Case study, finite element method and artificial neural network models for flow through Jeziorsko Earthfill dam in Poland. J Hydraul Eng 131(6):431–440. doi:10.1061/(ASCE)0733-9429(2005)131:6(431)

    Article  Google Scholar 

  20. Waszczyszyn Z, Ziemiański L (2001) Neural networks in mechanics of structures and materials–new results and prospects of applications. Comput Struct 79:2261–2276. doi:10.1016/S0045-7949(01)00083-9

    Article  Google Scholar 

  21. Deng XS, Wang XZ (2004) A neural network methodology for dam deformation predictions using historical displacements. Chin J Hydropower Autom Dam Monit 28(2):51–53

    Google Scholar 

  22. Li SJ, Liu YX, Liu YJ (2003) Dam deformation prediction by evolving artificial neural network. Chin J Rock Soil Mech 24(4):635–638

    Google Scholar 

  23. Mata J, Portela E, Dias J (2007) Application of neural networks to dam safety control. In: Pina C, Portela E, Gomes JP (eds) Proceedings of 5th international conference on dam engineering. LNEC, Lisbon, pp 315–324

  24. Yang J, Wu ZR, Gu CS (2001) Dam deformation monitoring model and forecast based on BP algorithm of artificial neural networks. Chin J Xi’an Univ Technol 17(1):25–29. doi:10.1016/S1006-1266(07)60006-6

    Article  MathSciNet  Google Scholar 

  25. Aussem A, Murtagh F (1997) Combining neural network forecasts on wavelet-transformed time series. Connect Sci 9(1):113–121. doi:10.1080/095400997116766

    Article  Google Scholar 

  26. Geva AB (1998) ScaleNet-Multiscale neural-network architecture for time series prediction. IEEE Trans Neural Netw 9(5):1471–1482. doi:10.1109/72.728396

    Article  Google Scholar 

  27. Aussem A, Murtagh F (2001) Wed traffic demand prediction using wavelet-based multiscale decomposition. Int J Intell Syst 16:215–236. doi:10.1002/1098-111X(200102)16:2<215::AID-INT50>3.0.CO;2-#

    Article  MATH  Google Scholar 

  28. Zhang BL, Coggins R, Jabri MA et al (2001) Multiresolution prediction for futures trading using wavelet decompositions. Trans Neural Netw 12:765–775. doi:10.1109/72.935090

    Article  Google Scholar 

  29. Zheng G, Strack JK, Campbell JG, Murtath F (1999) Multiscale transforms for filtering financial data streams. J Comput Intell Finance 7:18–35

    Google Scholar 

  30. Holschneider M, Kronland-Martinet R, Morlet J, Tchamitchian P (1989) Wavelets, time-frequency methods and phase space. In: A real-time algorithm for signal analysis with the help of the wavelet transform. Springer, Berlin, pp 289–297

    Google Scholar 

  31. Shensa MJ (1992) Discrete wavelet transforms, wedding the à trous and Mallat algorithms. Trans Signal Process 40(10):2464–2482. doi:10.1109/78.157290

    Article  MATH  Google Scholar 

  32. Cao M, Qiao P (2008) Neural network committee-based sensitivity analysis strategy for geotechnical engineering problems. Neural Comput Appl 17(5–6):509–519. doi:10.1007/s00521-007-0143-5

    Google Scholar 

  33. Hassibi B, Stork DG (1993) Second-order derivatives for network pruning, optimal brain surgeon. Adv Neural Inf Process Syst 5:164–171

    Google Scholar 

  34. Valsakumar MC, Satyanarayana SVM, Sridhar V (1997) Signature of chaos in power spectrum. Pramana 48(1):69–85. doi:10.1007/BF02845623

    Article  Google Scholar 

  35. Jang J-SR, Sun C-T, Mizutani E (1997) Neuro-fuzzy and soft computing, a computational approach to learning and machine intelligence. Prentice-Hall, Upper Saddle River

  36. Nørgaard M, Ravn O, Poulsen NK, Hansen LK (2000) Neural networks for modeling and control of dynamic systems. Springer, London

    Google Scholar 

  37. Zhang S, Liu HX, Gao DT, Du SD (2003) Determining the input dimension of a neural network for nonlinear time series prediction. Chin Phys 12(6):594–598. doi:10.1088/1009-1963/12/6/304

    Article  Google Scholar 

  38. Sragner L, Horvath G (2003) Improved model order estimation for nonlinear dynamic systems.In: Proceedings of the second IEEE international workshop on intelligent data acquisition and advanced computing systems, technology and applications, Lviv, pp 266–271

  39. MacKay D (1996) Bayesian non-linear modeling for the 1993 energy prediction competition in maximum entropy and Bayesian methods. In: Heidbreder G (ed) Kluwer, Dordrecht, pp 221–234

  40. Maier HR, Dandy GC (2001) Neural network based modelling of environmental variables: a systematic approach. Math Comput Model 33:669–682. doi:10.1016/S0895-7177(00)00271-5

    Article  MATH  Google Scholar 

  41. Duffy M, Hill C, Whitaker C, Chrzanowski A, Lutes J, Bastin G (2001) An automated and integrated monitoring program for Diamond Valley Lake in California. In: Proceedings of the 10th FIG international symposium on deformation measurements, Orange, pp K-1–K-23

Download references

Acknowledgments

This study is partially supported by the National Natural Science Foundations of China (NSFC) (Grant Numbers: 50539030 and 50608027) and the Science & Technology Foundation of Shandong Provincial Education Department (Grant Number: J07YE04-32426). The support provided by the Wood Materials and Engineering Laboratory (WMEL) at Washington State University to the first author is gratefully acknowledged.

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, College of Civil Engineering, Hohai University, 210098, Nanjing, Jiangsu, People’s Republic of China

    Maosen Cao, Pizhong Qiao & Qingwen Ren

  2. Department of Civil and Environmental Engineering, Washington State University, Pullman, WA, 99164-2910, USA

    Maosen Cao & Pizhong Qiao

  3. M. Cao College of Hydraulic and Civil Engineering, Shandong Agricultural University, 271018, Taian, Shandong, People’s Republic of China

    Maosen Cao

Authors
  1. Maosen Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Pizhong Qiao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Qingwen Ren
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Pizhong Qiao.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Cao, M., Qiao, P. & Ren, Q. Improved hybrid wavelet neural network methodology for time-varying behavior prediction of engineering structures. Neural Comput & Applic 18, 821–832 (2009). https://doi.org/10.1007/s00521-009-0240-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-009-0240-8

Keywords