Abstract
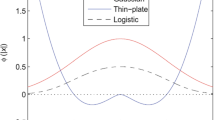
Radial basis function neural network (RBFNN) is widely used in nonlinear function approximation. One of the key issues in RBFNN modeling is to improve the approximation ability with samples as few as possible, so as to limit the network’s complexity. To solve this problem, a gradient-based sequential RBFNN modeling method is proposed. This method can utilize the gradient information of the present model to expand the sample set and refine the model sequentially, so as to improve the approximation accuracy effectively. Two mathematical examples and one practical problem are tested to verify the efficiency of this method.







Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Park J, Sandberg W (1991) Universal approximation using radial basis function networks. Neural Comput 3(2):246–257. doi:10.1162/neco.1991.3.2.246
Fang H, Horstemeyer (2005) Metamodeling with radial basis functions. In: The 46th AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics and materials conferrence, paper no. AIAA 2005-2059, Austin
Wu Z (1995) Compactly supported positive definite radial function. Adv Comput Math 4:283–292
Wendland H (1999) On the smoothness of positive definite and radial functions. J Comput Appl Math 101:177–188. doi:10.1016/S0377-0427(98)00218-0
Chen S, Cowan CF, Grant PM (1991) Orthogonal least square algorithm for radial basis function networks. IEEE Trans Neural Netw 2:302–309. doi:10.1109/72.80341
Xiaofang Y, Yaonan W, Wei S, Huiqian Y (2005) A hybrid learning algorithm for RBF neural networks based on support vector machines and BP algorithms. J Hunan Univ 32(3):88–92 in Chinese. Natural Sciences
Lin Y, Mistree F, Allen JK, Tsui KL, Chen VCP (2004) Sequential metamodeling in engineering design. In: The 10th AIAA/ISSMO multidisciplinary analysis and optimization conference, paper no. AIAA 2004-4304, Albany
Lin Y (2004) An efficient robust concept exploration method and sequential exploratory experimental design. PhD dissertation, Philosophy in Mechanical Engineering, Georgia Institute of Technology
Krishnamurthy T (2003) Response surface approximation with augmented and compactly supported radial basis functions. In: The 44th AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics, and materials conference, paper no. AIAA 2003-1748. Norfolk
Jin R, Chen W, Sudjianto A (2002) On sequential sampling for global metamodeling in engineering design. In: ASME 2002 design engineering technical conferences and computer and information in engineering conference, paper no. DETC2002/DAC-34092, Montreal
Yao W (2007) Research on uncertainty multidisciplinary design optimization theory and application to satellite system design (in Chinese). Master of engineering dissertation, National University of Defense Technology
Giunta AA, Wojtkiewicz SF Jr, Eldred MS (2003) Overview of modern design of experiments methods for computational simulations. In: 41st aerospace sciences meeting and exhibit, paper no. AIAA 2003-649, Reno
Giunta AA, Watson LT (1998) A comparison of approximation modeling techniques: polynomial versus interpolating models. In: The 7th AIAA/USAF/NASA/ISSMO symposium on multidisciplinary analysis and optimization, paper no. AIAA 98-4758, Louis
Author information
Authors and Affiliations
Corresponding author
Additional information
This article was originally presented in the fifth International Symposium on Neural Networks.
Rights and permissions
About this article
Cite this article
Yao, W., Chen, X. & Luo, W. A gradient-based sequential radial basis function neural network modeling method. Neural Comput & Applic 18, 477–484 (2009). https://doi.org/10.1007/s00521-009-0249-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-009-0249-z