Skip to main content

Advertisement

Springer Nature Link
Log in

An adaptive wavelet network for function learning

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

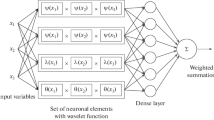
In this article, a wavelet neural network (WNN) model is proposed for approximating arbitrary nonlinear functions. Our WNN model structure comes from the idea of adaptive neuro-fuzzy inference system (ANFIS) which is used for obtaining fuzzy rule base from the input–output data of an unknown function. The WNN model which is called in this study as adaptive wavelet network (AWN) consists of wavelet scaling functions in its processing units whereas in an ANFIS, mostly Gaussian-type membership functions are used for a function approximation. We present to train an AWN by a hybrid-learning method containing least square estimation (LSE) with gradient-based optimization algorithm to obtain the optimal translation and dilation parameters of our AWN for model accuracy. Simulation examples are also given to illustrate the effectiveness of the method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Zhang Q (1997) Using wavelet networks in nonparametric estimation. IEEE Trans Neural Netw 8:227–336. doi:10.1109/72.557660

    Article  Google Scholar 

  2. Zhang Q, Benveniste A (1992) Wavelet networks. IEEE Trans Neural Netw 3:889–898. doi:10.1109/72.165591

    Article  Google Scholar 

  3. Zhang J, Walter GG, Lee WNW (1995) Wavelet neural networks for function learning. IEEE Trans Signal Process 43:1485–1497. doi:10.1109/78.388860

    Article  Google Scholar 

  4. Ho Daniel WC, Zhang PA, Jinhua X (2001) Fuzzy wavelet networks for function learning. IEEE Trans Fuzzy Syst 9:200–211. doi:10.1109/91.917126

    Article  Google Scholar 

  5. Kim J, Kasabov N (1999) HyFIS: adaptive neuro-fuzzy inference systems and their application to nonlinear dynamical systems. Neural Netw 12:1301–1319. doi:10.1016/S0893-6080(99)00067-2

    Article  Google Scholar 

  6. Jang JSR (1993) ANFIS: adaptive-network-based fuzzy inference systems. IEEE Trans Syst Man Cybern 23(3):665–685. doi:10.1109/21.256541

    Article  MathSciNet  Google Scholar 

  7. Horikawa S, Furuhashi T, Uchikawa Y (1992) On fuzzy modeling using fuzzy neural networks with the back-propagation algorithm. IEEE Trans Neural Netw 3(5):801–806. doi:10.1109/72.159069

    Article  Google Scholar 

  8. Leonard J, Kramer M (1991) Radial basis function networks for classifying process faults. IEEE Control Syst 11:31–38. doi:10.1109/37.75576

    Article  Google Scholar 

  9. Tan Y, Dang X, Liang F, Su CY (2000) Dynamic wavelet neural network for nonlinear dynamic system identification. In: Proceedings of the 2000 IEEE, international conference on control applications

  10. Mallat S (1989) A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans Pattern Anal Mach Intell 11(7):674–693. doi:10.1109/34.192463

    Article  MATH  Google Scholar 

  11. Sanner R, Slotine J-JE (1992) Gaussian networks for direct adaptive control. IEEE Trans Neural Netw 13(6):837–863. doi:10.1109/72.165588

    Article  Google Scholar 

  12. Ljung L (1987) System identification: theory for the user. Prentice-Hall, Englewood Cliffs

    MATH  Google Scholar 

  13. Strobach P (1990) Linear prediction theory: a mathematical basis for adaptive systems. Springer, New York

    MATH  Google Scholar 

  14. Gholizadeh S, Salajegheh E, Torkzadeh P (2008) Structural optimization with frequency constraints by genetic algorithm using wavelet radial basis function neural network. J Sound Vibrat 312:316–331. doi:10.1016/j.jsv.2007.10.050

    Article  Google Scholar 

  15. Gill PE, Murray W, Wright MH (1993) Practical optimization. Academic Press Ltd, London

    Google Scholar 

  16. Chen J, Bruns DD (1995) WaveARX neural network development for system identification using a systematic design synthesis. Ind Eng Chem Res 34:4420–4435. doi:10.1021/ie00039a034

    Article  Google Scholar 

  17. Box GEP (1970) Time series analysis, forecasting and control. Holden Day, San Francisco

    MATH  Google Scholar 

  18. Chen Y, Yang B, Dong J (2006) Time-series prediction using a local linear wavelet neural network. Neurocomputing 69:449–465. doi:10.1016/j.neucom.2005.02.006

    Article  Google Scholar 

  19. Tong RM (1980) The evaluation of fuzzy models derived from experimental data. Fuzzy Sets Syst 4:1–12. doi:10.1016/0165-0114(80)90059-7

    Article  MATH  Google Scholar 

  20. Pedrycz W (1984) An identification algorithm in fuzzy relational systems. Fuzzy Sets Syst 13:153–167. doi:10.1016/0165-0114(84)90015-0

    Article  MATH  MathSciNet  Google Scholar 

  21. Xu CW (1987) Fuzzy model identification and self-learning for dynamic systems. IEEE Trans Syst Man Cybern 17:683–689. doi:10.1109/TSMC.1987.289361

    Article  MATH  Google Scholar 

  22. Sugeno M et al (1991) Linguistic modeling based on numerical data. Proc IFSA 91:234–247

    Google Scholar 

  23. Surmann H et al (1993) Self-organizing and genetic algorithm for an automatic design of fuzzy control and decision systems. Proc FUFIT’s 93:1079–1104

    Google Scholar 

  24. Jang JSR et al (1997) Neuro-fuzzy and Soft computing: a computational approach to learning and machine intelligence. Prentice-Hall, Upper Saddle river

    Google Scholar 

  25. Kasabov NK et al (1997) FuNN/2-A fuzzy neural network architecture for adaptive learning and knowledge acquisition. Inf Sci 101:155–175. doi:10.1016/S0020-0255(97)00007-8

    Article  Google Scholar 

  26. Chen YH et al (2004) Nonlinear system modeling via optimal design of neural trees. Int J Neural Syst 14(2):125–137. doi:10.1142/S0129065704001905

    Article  Google Scholar 

  27. Mackey M, Glass L (1977) Oscillation and chaos in physiological control systems. Science 197:287–289. doi:10.1126/science.267326

    Article  Google Scholar 

  28. Wang LX et al (1992) Generating fuzzy rules by learning from examples. IEEE Trans Fuzzy Syst Man Cybern 22:1414–1427. doi:10.1109/21.199466

    Article  Google Scholar 

  29. Cho KB et al (1995) Radial basis function based adaptive fuzzy systems their application to system identification and prediction. Fuzzy Sets Syst 83:325–339. doi:10.1016/0165-0114(95)00322-3

    Article  Google Scholar 

  30. Rojas I et al (2002) Time series analysis using normalized PG-RBF network with regression weights. Neurocomputing 42:167–285. doi:10.1016/S0925-2312(01)00338-1

    Article  Google Scholar 

  31. Kim D et al (1997) Forecasting time series with genetic fuzzy predictor ensembles. IEEE Trans Fuzzy Syst 5(2):523–535

    Google Scholar 

  32. Narendra KS, Parthasarathy K (1990) Identification and control dynamical systems using neural networks. IEEE Trans Neural Netw 1(1):4–27. doi:10.1109/72.80202

    Article  Google Scholar 

  33. Abiyev RH, Kaynak O (2008) Fuzzy wavelet neural network for identification and control of dynamic plants—a novel structure and comparative study. IEEE Trans Ind Electron 55(8):3133–3140. doi:10.1109/TIE.2008.924018

    Article  Google Scholar 

  34. Elman JL (1990) Finding structure in time. Cogn Sci 14(2):179–211

    Article  Google Scholar 

  35. Juang CF, Lin CT (1999) A recurrent self-organizing neural fuzzy inference network. IEEE Trans Neural Netw 10(4):828–845. doi:10.1109/72.774232

    Article  Google Scholar 

  36. Juang C-F (2002) A TSK-type recurrent fuzzy network for dynamic systems processing by neural network and genetic algorithms. IEEE Trans Fuzzy Syst 10(2):155–170. doi:10.1109/91.995118

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Engineering, Faculty of Engineering and Architecture, Anadolu University, 26555, Eskisehir, Turkey

    Yusuf Oysal & Sevcan Yilmaz

Authors
  1. Yusuf Oysal
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Sevcan Yilmaz
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Sevcan Yilmaz.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Oysal, Y., Yilmaz, S. An adaptive wavelet network for function learning. Neural Comput & Applic 19, 383–392 (2010). https://doi.org/10.1007/s00521-009-0297-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-009-0297-4

Keywords