Skip to main content

Advertisement

Springer Nature Link
Log in

Feature space versus empirical kernel map and row kernel space in SVMs

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

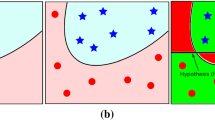
In machine-learning technologies, the support vector machine (SV machine, SVM) is a brilliant invention with many merits, such as freedom from local minima, the widest possible margins separating different clusters, and a solid theoretical foundation. In this paper, we first explore the linear separability relationships between the high-dimensional feature space H and the empirical kernel map U as well as between H and the space of kernel outputs K. Second, we investigate the relations of the distances between separating hyperplanes and SVs in H and U, and derive an upper bound for the margin width in K. Third, as an application, we show experimentally that the separating hyperplane in H can be slightly adjusted through U. The experiments reveal that existing SVM training can linearly separate the data in H with considerable success. The results in this paper allow us to visualize the geometry of H by studying U and K.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Burges CJC (1998) A tutorial on support vector machines for pattern recognition. Data Min Knowl Discov 2:121–167. doi:10.1023/A:1009715923555

    Article  Google Scholar 

  2. Camps-Valls G, Bruzzone L (2005) Kernel-based methods for hyperspectral image classification. IEEE Trans Geosci Rem Sens 43:1–12. doi:10.1109/TGRS.2005.846154

    Article  Google Scholar 

  3. Chang C-C, Lin C-J (2008) LIBSVM: a library for support vector machines, 2001. (Software available at http://www.csie.ntu.edu.tw/˜cjlin/libsvm), 2008-11-30

  4. Chang C-C, Lin C-J (2008) LIBSVM FAQ, http://www.csientu.edu.tw/~cjlin/libsvm/faq.html#faq1., 2008-11-30

  5. Chang M, Lin C (2005) Leave-one-out bounds for support vector regression model selection. Neural Comput 17:1188–1222. doi:10.1162/0899766053491869

    Article  MATH  Google Scholar 

  6. Chen P-H, Fan R-E, Lin C-J (2006) A study on SMO-type decomposition methods for support vector machines. IEEE Trans Neural Netw 17:893–908. doi:10.1109/TNN.2006.875973

    Article  Google Scholar 

  7. Cristianini N, Shawe-Taylor J (2000) An introduction to support vector machines and other kernel-based learning methods. Cambridge University Press, Cambridge

    Google Scholar 

  8. Fan R-E, Chen P-H, Lin C-J (2005) Working set selection using second order information for training SVM. J Mach Learn Res 6:889–1918

    MathSciNet  Google Scholar 

  9. Fine S, Scheinberg K (2001) Efficient SVM training using low-rank kernel representations. J Mach Learn Res 2:243–264. doi:10.1162/15324430260185619

    Article  Google Scholar 

  10. Google search, with keywords “LibSVM” and “experiment” subject to the PDF file format: http://www.google.cn/search?as_q=LibSVM&hl=zh-CN&newwindow=1&num=100&btnG=Google+%E6%90%9C%E7%B4%A2&as_epq=experiment&as_oq=&as_eq=&lr=lang_en&as_ft=i&as_filetype=pdf&as_qdr=all&as_occt=any&as_dt=i&as_sitesearch=&as_rights=, Sept 30 2008

  11. Google search, with keywords “SVMlight” and “experiment” subject to the PDF file format: http://www.google.cn/search?as_q=SVMlight&complete=1&hl=zh-CN&newwindow=1&num=100&btnG=Google+%E6%90%9C%E7%B4%A2&as_epq=experiment&as_oq=&as_eq=&lr=&as_ft=i&as_filetype=pdf&as_qdr=all&as_occt=any&as_dt=i&as_sitesearch=&as_rights=, Sept 30 2008

  12. Google search, with keywords “SVMTorch” and “experiment” subject to the PDF file format: http://www.google.cn/search?as_q=SVMTorch&hl=zh-CN&newwindow=1&num=100&btnG=Google+%E6%90%9C%E7%B4%A2&as_epq=experiment&as_oq=&as_eq=&lr=&as_ft=i&as_filetype=&as_qdr=all&as_occt=any&as_dt=i&as_sitesearch=&as_rights=, Sept 30 2008

  13. Google search, with keywords “Matlab SVM” and “experiment” subject to the PDF file format: http://www.google.cn/search?as_q=experiment&hl=zh-CN&newwindow=1&num=100&btnG=Google+%E6%90%9C%E7%B4%A2&as_epq=matlab+svm&as_oq=&as_eq=&lr=&as_ft=i&as_filetype=pdf&as_qdr=all&as_occt=any&as_dt=i&as_sitesearch=&as_rights=, Sept 30 2008

  14. Kohavi R, Becker B (2008) http://archive.ics.uci.edu/ml/datasets/Adult. Sept 30 2008

  15. Hastie T, Rosset S, Tibshirani R, Zhu J (2004) The entire regularization path for the support vector machine. J Mach Learn Res 5:1391–1415

    MathSciNet  Google Scholar 

  16. Liang F (2003) An effective Bayesian neural network classifier with a comparison study to support vector machine. Neural Comput 15:1959–1989. doi:10.1162/08997660360675107

    Article  MATH  Google Scholar 

  17. Liang X, Chen R, Guo X (2008) Pruning support vector machines without altering performances. IEEE Trans Neural Netw 19:1792–1803. doi:10.1109/TNN.2008.2002696

    Article  Google Scholar 

  18. Lin C-J (2002) Asymptotic convergence of an SMO algorithm without any assumptions. IEEE Trans Neural Netw 13:248–250. doi:10.1109/72.977319

    Article  Google Scholar 

  19. Musicant DR, Feinberg A (2004) Active set support vector regression. IEEE Trans Neural Netw 15:268–275. doi:10.1109/TNN.2004.824259

    Article  Google Scholar 

  20. Platt JC (1998) Fast training of support vector machines using sequential minimal optimization. In: Scholkopf B, Burges CJC, Smola AJ (eds) Advances in kernel methods—support vector learning. MIT Press, Cambridge, pp 41–65

    Google Scholar 

  21. Pontil M, Verri A (1998) Properties of support vector machines. Neural Comput 10:955–974. doi:10.1162/089976698300017575

    Article  Google Scholar 

  22. Scholkopf B, Mika S, Burges CJC, Knirsch P, Muller K-R, Ratsch G, Smola AJ (1999) Input space versus feature space in kernel-based methods. IEEE Trans Neural Netw 10:1000–1017. doi:10.1109/72.788641

    Article  Google Scholar 

  23. Vapnik V (1995) The nature of statistical learning theory. Springer-Verlag, New York

    MATH  Google Scholar 

  24. Vapnik V, Chapelle O (2000) Bounds on error expectation for support vector machines. Neural Comput 12:2013–2036. doi:10.1162/089976600300015042

    Article  Google Scholar 

  25. Zhang L, Zhou W, Jiao L (2004) Hidden space support vector machines. IEEE Trans Neural Netw 15:1424–1434. doi:10.1109/TNN.2004.831161

    Article  Google Scholar 

Download references

Acknowledgments

The authors thank the anonymous reviewers for their valuable comments and suggestions, which helped improve the paper greatly. The project was sponsored by the NSF of China under grants 70571003 and 70871001, and the 863 Project of China under grant 2007AA01Z437.

Author information

Authors and Affiliations

  1. Department of Economic Information Management, Remin University of China, 100872, Beijing, China

    Xun Liang

  2. Department of Economics and Operations Research, Stanford University, Stanford, CA, 95035, USA

    Xun Liang

Authors
  1. Xun Liang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xun Liang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liang, X. Feature space versus empirical kernel map and row kernel space in SVMs. Neural Comput & Applic 19, 487–498 (2010). https://doi.org/10.1007/s00521-010-0337-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-010-0337-0

Keywords