Skip to main content

Advertisement

Springer Nature Link
Log in

An immune-inspired multi-objective approach to the reconstruction of phylogenetic trees

  • AIS
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

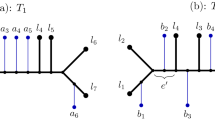
Abstract

This work presents the application of the omni-aiNet algorithm—an immune-inspired algorithm originally developed to solve single and multi-objective optimization problems—to the reconstruction of phylogenetic trees. The main goal here is to automatically evolve a population of phylogenetic unrooted trees, possibly with distinct topologies, by minimizing at the same time two optimization criteria: the minimum evolution and the mean-squared error. This proposal generates, in a single run, a set of non-dominated solutions that represent the trade-offs of the two conflicting objectives, and gives the user the possibility of having distinct explanations for the differences observed at the terminal nodes of the trees. A series of experimental results is also reported in this work, in order to illustrate the effectiveness of the proposal and its capability to overcome the restrictive feedback provided by the application of well-known algorithms for phylogenetic reconstruction, such as the Neighbor Joining. Besides, the methodology presented in this work is compared to the popular NSGA-II algorithm, also modified to solve phylogenetic reconstruction problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Notes

  1. These two criteria were selected in this work because they are two of the most popular ones in the algorithms for phylogenetic reconstruction based on distance matrices. However, the proposed methodology can be easily extended to consider two or more different criteria.

References

  1. Smith JM (1993) The theory of evolution. Cambridge University Press, Cambridge

    Google Scholar 

  2. Darwin C (1859) On the origin of species by means of natural selection, or the preservation of favoured races in the struggle for life. John Murray, London

    Google Scholar 

  3. Felsenstein J (2004) Inferring phylogenies. Sinauer Associates, Suderland

    Google Scholar 

  4. Kidd KK, Sgaramella-Zonta LA (1971) Phylogenetic analysis: concepts and methods. Am J Hum Genet 23:235–252

    Google Scholar 

  5. Bulmer M (1991) Use of the method of generalized least squares in reconstructing phylogenies from sequence data. Mol Biol Evol 8:868–883

    Google Scholar 

  6. Saitou N, Nei M (1987) The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol Biol Evol Evolution 4(4):406–425

    Google Scholar 

  7. Takahashi K, Nei M (2000) Efficiencies of fast algorithms of phylogenetic inference under the criteria of maximum parsimony, minimum evolution, and maximum likelihood when a large number of sequences are used. Mol. Biol. Evol. 17(8):1251–1258

    Google Scholar 

  8. Eschenauer H, Koski J, Osyczka A (1990) Multicriteria design optimization: procedures and applications. Springer, Berlin

    MATH  Google Scholar 

  9. Statnikov RB, Matusov JB (1995) Multicriteria optimization and engineering. Chapman & Hall, New York

    Google Scholar 

  10. Miettinen KM (1999) Nonlinear multiobjective optimization. Kluwer, Boston

    MATH  Google Scholar 

  11. Ehrgott M (2005) Multicriteria optimization. Springer, Berlin

    MATH  Google Scholar 

  12. Deb K (2001) Multi-objective optimization using evolutionary algorithms. Wiley, Chichester

    MATH  Google Scholar 

  13. Coello Coello CA, Van Veldhuizen DA, Lamont GB (2002) Evolutionary algorithms for solving multi-objective problems. Kluwer, New York

    MATH  Google Scholar 

  14. Coello Coello CA, Cruz Cortes N (2005) Solving multiobjective optimization problems using an artificial immune system. Genet Program Evol Mach 6:163–190

    Article  Google Scholar 

  15. Coelho GP, Von Zuben FJ (2006) omni-aiNet: an immune-inspired approach for omni optimization. In: Proceedings of the fifth international conference on artificial immune systems, Oeiras, Portugal, September 2006, pp 294–308

  16. Coelho GP, da Silva AE, Von Zuben FJ (2007) Evolving phylogenetic trees: a multiobjective approach. In: Proceedings of the Brazilian symposium on bioinformatics. Angra dos Reis, Brazil, August 2007, pp 113–125

  17. Nei M, Kumar S (2000) Molecular evolution and phylogenetics. Oxford University Press, New York

    Google Scholar 

  18. Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197

    Article  Google Scholar 

  19. Poladian L, Jermiin LS (2004) What might evolutionary algorithms (EA) and multi-objective optimisation (MOO) contribute to phylogenetics and the total evidence debate. In: Proceedings of the genetic and evolutionary computing conference (GECCO 2004). Seattle

  20. Poladian L, Jermiin LS (2006) Multi-objective evolutionary algorithms and phylogenetic inference with multiple data sets. Soft Comput 4(10):359–368

    Article  Google Scholar 

  21. Huelsenbeck JP, Crandall KA (1997) Phylogeny estimation and hypothesis testing using maximum likelihood. Annu Rev Ecol Syst 28:437–466

    Article  Google Scholar 

  22. Holmes SP (1999) Phylogenies: an overview. Stat Genet 112:81–119

    Google Scholar 

  23. Day WHE (1987) Computational complexity of inferring phylogenies from dissimilarity matrices. Bull Math Biol 49:461–467

    MATH  MathSciNet  Google Scholar 

  24. Billera LJ, Holmes SP, Vogtmann K (2001) Geometry of the space of phylogenetic trees. Adv Appl Math 27(4):733–767

    Article  MATH  MathSciNet  Google Scholar 

  25. Roch S (2006) A short proof that phylogenetic tree reconstruction by maximum likelihood is hard. IEEE/ACM Trans Comput Biol Bioinf 3(1):92

    Article  MathSciNet  Google Scholar 

  26. Sneath PHA, Sokal RR (1973) Numerical taxonomy. Freeman, San Francisco

    MATH  Google Scholar 

  27. Fitch WM, Margoliash E (1967) Construction of phylogenetic trees. Science 155:279–284

    Article  Google Scholar 

  28. Saitou N, Imanishi T (1989) Relative efficiencies of the Fitch-Margoliash, maximum-parsimony, maximum-likelihood, minimum-evolution, and neighbor-joining methods of phylogenetic tree construction in obtaining the correct tree. Mol Biol Evol 6(5):514–525

    Google Scholar 

  29. DasGupta B, He X, Jiang T, Li M, Tromp J, Zhang L (1997) On distances between phylogenetic trees. In: Proceedings of the 8th annual ACM—SIAM symposium on discrete algorithms, pp 427–436

  30. Brodal GS, Fagerberger R, Pedersen CNS (2004) Computing the quartet distance between evolutionary trees in time O(n.log(n)). Algorithmica 38:377–395

    Article  MATH  MathSciNet  Google Scholar 

  31. DasGupta B, He X, Jiang T, Li M, Tromp J, Zhang L (2000) On computing the nearest neighbor interchange distance. In: Du D-Z, Pardalos PM, Wang J (eds) Discrete mathematical problems with medical applications, vol 55 of DIMACS series in discrete mathematics and theoretical computer science. Am Math Soc, pp 125–143

  32. Bryant D (2003) A classification of consensus methods for phylogenetics. In: Janowitz MF, Lapoint FJ, Morris FR, Mirkin B, Roberts FS (eds) Bioconsensus, vol 61 of DIMACS series in discrete mathematics and theoretical computer science. Am Math Soc, pp 163–184

  33. Robinson DF, Foulds LR (1981) Comparison of phylogenetic trees. Math Biosci 53:131–147

    Article  MATH  MathSciNet  Google Scholar 

  34. Edgeworth FY (1881) Mathematical physics. P. Keagan, London

    Google Scholar 

  35. Pareto V (1896) Cours D’Economie politique. F. Rouge, Lausanne

  36. Goldberg DE (1989) Genetic algorithms in search, optimization and machine learning. Addison-Wesley Publishing Company, Reading

    MATH  Google Scholar 

  37. Bäck T, Fogel DB, Michalewicz Z (eds) (2000) Evolutionary computation 1: basic algorithms and operators Institute of Physics Publishing, Bristol

    MATH  Google Scholar 

  38. Bäck T, Fogel DB, Michalewicz Z (eds) (2000) Evolutionary computation 2: advanced algorithms and operators. Institute of Physics Publishing, Bristol

    MATH  Google Scholar 

  39. Coello Coello CA (1999) A comprehensive survey of evolutionary-based multiobjective optimization techniques. Knowl Inf Syst 1(3):129–156

    Google Scholar 

  40. Coello Coello CA (2006) Evolutionary multi-objective optimization: a historical view of the field. IEEE Comput Intell Mag 1(1):28–36

    Article  MathSciNet  Google Scholar 

  41. Zitzler E, Thiele L (1999) Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput 3(4):257–271

    Article  Google Scholar 

  42. Corne DW, Knowles JD, Oates MJ (2000) The Pareto envelope-based selection algorithm for multiobjective optimization. In: Proceedings of the parallel problem solving from nature VI conference, pp 839–848

  43. Knowles JD, Corne DW (2000) Approximating the nondominated front using the Pareto archived evolution strategy. Evol Comput 8(2):149–172

    Article  Google Scholar 

  44. Coello Coello CA, Toscano Pulido G (2001) Multiobjective optimization using a micro-genetic algorithm. In: Proceedings of the genetic and evolutionary computation conference, (GECCO’2001), San Francisco, pp 274–282

  45. Corne DW, Jerram NR, Knowles JD, Oates MJ (2001) PESA-II: region-based selection in evolutionary multiobjective optimization. In: Proceedings of the genetic and evolutionary computation conference (GECCO-2001), San Francisco, pp 283–290

  46. Zitzler E, Laumanns M, Thiele L (2002) SPEA2: Improving the strength Pareto evolutionary algorithm. In: EUROGEN 2001. Evolutionary methods for design, optimization and control with applications to industrial problems. pp 95–100

  47. de Castro LN, Von Zuben FJ (2005) Recent developments in biologically inspired computing. IGI Publishing, Hershey

    Google Scholar 

  48. de Castro LN, Timmis J (2002) An introduction to artificial immune systems: a new computational intelligence paradigm. Springer, Berlin

    Google Scholar 

  49. Jerne NK (1974) Towards a network theory of the immune system. Annu Immunol Inst Pasteur 125:373–389

    Google Scholar 

  50. Burnet FM (1978) Clonal selection and after. In: Bell GI, Perelson AS, Pimgley GH Jr. (eds) Theoretical immunology. Marcel Dekker Inc, New York, pp 63–85

    Google Scholar 

  51. Sareni B, Krähenbühl L (1998) Fitness sharing and niching methods revisited. IEEE Trans Evol Comput 2(3):97–106

    Article  Google Scholar 

  52. Freschi F, Repetto M (2005) Multiobjective optimization by a modified artificial immune system algorithm. In: Proceedings of the 4th international conference on artificial immune systems (ICARIS), Banff, pp 248–261

  53. Jiao L, Gong M, Shang R, Du H, Lu B (2005) Clonal selection with immune dominance and anergy based multiobjective optimization. In: Proceedings of the 3rd international conference on evolutionary multi-criterion optimization (EMO), Guanajuato, pp 474–489

  54. Lu B, Jiao L, Du H, Gong M (2005) IFMOA: Immune forgetting multiobjective optimization algorithm. In: Proceedings of the 1st international conference on natural computation (ICNC), Changsha, pp 399–408

  55. Shang R, Ma W (2006) Immune clonal MO algorithm for ZDT problems. In: Proceedings of the 2nd international conference on natural computation (ICNC), Xi’an, pp 100–109

  56. Castro PAD, Von Zuben FJ (2008) MOBAIS: A bayesian artificial immune system for multi-objective optimization. In: Bentley P, Lee D, Jung S (eds) Proceedings of the 7th international conference on artificial immune system vol. 5132 of lecture notes in computer science, Phuket, pp 48–59

  57. Deb K, Tiwari S (2005) Omni-optimizer: a procedure for single and multi-objective optimization. In: Proceedings of the 3rd international conference on evolutionary multi-criterion optimization (EMO), Guanajuato, pp 47–61

  58. de Castro LN, Von Zuben FJ (2001) aiNet: an artificial immune network for data analysis. In: Abbass HA, Sarker RA, Newton CS (eds) Data mining: a heuristic approach. Idea Group Publishing, pp 231–259

  59. de Castro LN, Timmis J (2002) An artificial immune network for multimodal function optimization. In: Proceedings of the IEEE conference on evolutionary computation (CEC), Honolulu, pp 699–704

  60. de Castro LN, Von Zuben FJ (2002) Learning and optimization using the clonal selection principle. IEEE Trans Evol Comput 6(3):239–251

    Article  Google Scholar 

  61. Gomes LCT, de Sousa JS, Bezerra GB, de Castro LN, Von Zuben FJ (2003) Copt-ainet and the gene ordering problem. Inf Technol Mag, Cathol Univ Brasília 3(2):27–33

    Google Scholar 

  62. de França FO, Von Zuben FJ, de Castro LN (2005) An artificial immune network for multimodal function optimization on dynamic environments. In: Proceedings of the genetic and evolutionary computation conference (GECCO), Washington, pp 289–296

  63. Castro PAD, de França FO, Ferreira HM, Von Zuben FJ (2007) Applying biclustering to text mining: an immune-inspired approach. In: Proceedings of the 6th international conference on artificial immune systems (ICARIS), Santos, pp 83–94

  64. Rudolph G, Agapie A (2000) Convergence properties of some multi-objective evolutionary algorithms. In: Proceedings of the IEEE conference on evolutionary computation (CEC), Piscataway, pp 1010–1016

  65. Ohno S (1970) Evolution by gene duplication. Allen and Unwin, London

    Google Scholar 

  66. Holland PWH, Garcia-Fernandez J, Williams NA, Sidow A (1994) Gene duplications and the origins of vertebrate development. Development (Suppl):125–133

  67. Felsenstein J. The Newick tree format. http://evolution.genetics.washington.edu/phylip/newicktree.html. Accessed 28 june 2010

  68. Atteson K (1999) The performance of neighbor-joining methods of phylogenetic reconstruction. Algorithmica 25:251–278

    Article  MATH  MathSciNet  Google Scholar 

  69. Tamura K, Dudley J, Nei M, Kumar S (2007) MEGA4: molecular evolutionary genetics analysis (MEGA) software version 4.0. Mol Biol Evol 24:1596–1599

    Article  Google Scholar 

  70. Bartélemy JP, Guénoche A (1991) Trees and proximity representations. Wiley, Chichester

    Google Scholar 

  71. Faiger H, Ivanchenko M, Haran TE (2007) Nearest-neighbor non-additivity versus long-range non-additivity in TATA-box structure and its implications for TBP-binding mechanism. Nucleic Acids Res 35(13):4409–4419

    Google Scholar 

  72. Carleton MD (1988) Systematics and evolution. In: Kirkland GL Jr, Layne JN (eds) Advances in the study of Peromyscus (Rodentia). Texas Tech University Press, TX, pp 7–140

  73. Bermingham E, Moritz C (1998) Comparative phylogeography: concepts and applications. Mol Ecol 7:367–369

    Article  Google Scholar 

  74. MacLeod N, Forey PL (eds) (2002) Morphology, shape and phylogeny. Systematics association special volume. Taylor & Francis, UK

    Google Scholar 

  75. da Silva AEA, Villanueva WJP, Knidel H, Bonato V, dos Reis SF, Von Zuben FJ (2005) A multi-neighbor-joining approach for phylogenetic tree reconstruction and visualization. Genet Mol Res 4(3):525–534

    Google Scholar 

  76. Bonato V (2004) Patterns of geographic variation in Thrichomys apereoides (Rodentia: Echimyidae). PhD thesis (in Portuguese), Department of Ecology, University of Campinas, Campinas

  77. Zitzler E (1999) Evolutionary Algorithms for Multiobjective Optimization. PhD thesis, Swiss Federal Institute of Technology, Zürich

Download references

Acknowledgments

The authors would like to thank Prof. Sérgio Furtado dos Reis for providing the distance matrix of the Trichomys apereoides problem, and CAPES and CNPq for the financial support.

Author information

Authors and Affiliations

  1. Laboratory of Bioinformatics and Bioinspired Computing (LBiC), Department of Computer Engineering and Industrial Automation (DCA), School of Electrical and Computer Engineering (FEEC), University of Campinas (Unicamp), Av. Albert Einstein, 400, Building G2, Room LE 14G, Cidade Universitária Zeferino Vaz, Barão Geraldo, Campinas, SP, 13083-852, Brazil

    Guilherme P. Coelho & Fernando J. Von Zuben

  2. School of Mathematical and Nature Sciences, Methodist University of Piracicaba (UNIMEP), Rodovia do Açúcar km 156, Piracicaba, SP, 13.400-911, Brazil

    Ana Estela A. da Silva

Authors
  1. Guilherme P. Coelho
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ana Estela A. da Silva
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Fernando J. Von Zuben
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Guilherme P. Coelho.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Coelho, G.P., da Silva, A.E.A. & Von Zuben, F.J. An immune-inspired multi-objective approach to the reconstruction of phylogenetic trees. Neural Comput & Applic 19, 1103–1132 (2010). https://doi.org/10.1007/s00521-010-0389-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-010-0389-1

Keywords