Skip to main content
Springer Nature Link
Log in

Internal model control based on a novel least square support vector machines for MIMO nonlinear discrete systems

  • ISNN 2010
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

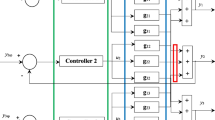
To improve the robustness of the traditional inverse system method, the internal model control based on a novel least square support vector machines (LS-SVM) is proposed. The novel LS-SVM considers general errors that include noises of input variables and output variables as empirical errors. The data of original MIMO discrete system is exploited to approximate its inverse model by the novel LS-SVM. By cascading the inverse model and the original system to constitute a decoupling pseudo-linear system, the internal model control strategy is carried out to the pseudo-linear system to realize the effective control. Simulation validates that the novel LS-SVM used in the inverse system identification is effective and shows that the internal model control of nonlinear discrete systems has better robustness of anti-interference and parameters varying than that of the open-loop system only based on inverse control.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Lightbody G, Irwin GW (1997) Nonlinear control structures based on embedded neural system models. IEEE Trans Neural Netw 8(3):553–567

    Article  Google Scholar 

  2. Rivals I, Personnaz L (2000) Nonlinear internal model control using neural networks: application to processes with delay and design issues. IEEE Trans Neural Netw 11(1):80–90

    Article  Google Scholar 

  3. Li M, Zhou ZK, Shi LL (2004) The neural network decoupling control based on the internal model control. In: Proceedings of the 5th world congress on intelligent control and automation, Hangzhou, China, pp 2643–2646

  4. Haber RE, Alique JR (2004) Nonlinear internal model control using neural networks: an application for machining processes. Neural Comput Appl 13:47–55

    Article  Google Scholar 

  5. Chidrawar SK, Patre BM (2008) Implementation of neural network for internal model control and adaptive control. In: Proceedings of the international conference on computer and communication engineering, Kuala Lumpur, Malaysia, pp 741–746

  6. Cui WT, Yan XF (2009) Adaptive weighted least square support vector machine regression integrated with outlier detection and its application in QSAR. Chemom Intell Lab Syst 98:130–135

    Article  Google Scholar 

  7. Vapnik VN (1998) Statistical learning theory. Wiley, NewYork

    Google Scholar 

  8. Evgeniou T, Pontil M, Poggio T (2000) Regularization networks and support vector machiness. Adv Comput Math 13(1):1–50

    Article  MathSciNet  Google Scholar 

  9. Suykens JAK, Vandewalle J (1999) Least squares support vector machines classifiers. Neural Process Lett 9(3):293–300

    Article  MathSciNet  Google Scholar 

  10. Suykens, JAK, Lukas L, Vandewalle J (2000) Sparse approximation using least-squares support vector machines. In: Proceedings of the IEEE international symposium on circuits and systems, Geneva, Switzerland, pp 11757–11760

  11. Markovsky I, VanHuffel S (2007) Overview of total least squares methods. Signal Process 87:2283–2302

    Article  Google Scholar 

  12. Peng XJ, Wang YF (2009) A normal least squares support vector machine (NLS-SVM) and its learning algorithm. Neurocomputing 72:3734–3741

    Article  Google Scholar 

  13. Dai XZ (2005) Inverse control method based on neural networks for multi-variables nonlinear system (in Chinese). Science Press, Beijing

    Google Scholar 

  14. Sun CY, Mu CX, Li XM (2009) A weighted LS-SVM approach for the identification of a class of nonlinear inverse systems. Sci China Ser F Inf Sci 52(5):770–779

    Article  MathSciNet  Google Scholar 

  15. Suykens JAK, Brabanter JD, Lukas L, Vandewalle J (2002) Weighted least squares support vector machiness: robustness and sparse approximation. Neurocomputing 48:85–105

    Article  Google Scholar 

  16. Garcia CE, Morari M (1982) Internal model control: a unifying review and some new results. Ind Eng Chem Process Des 21(2):308–323

    Article  Google Scholar 

Download references

Acknowledgments

This work has been supported by the National Natural Science Foundation of China (No. 60874013 and No. 60953001).

Author information

Authors and Affiliations

  1. School of Automation, Southeast University, Nanjing, 210096, China

    Chaoxu Mu, Changyin Sun & Xinghuo Yu

Authors
  1. Chaoxu Mu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Changyin Sun
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xinghuo Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Changyin Sun.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mu, C., Sun, C. & Yu, X. Internal model control based on a novel least square support vector machines for MIMO nonlinear discrete systems. Neural Comput & Applic 20, 1159–1166 (2011). https://doi.org/10.1007/s00521-010-0468-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-010-0468-3

Keywords