Skip to main content

Advertisement

Springer Nature Link
Log in

Approximation of algebraic and trigonometric polynomials by feedforward neural networks

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

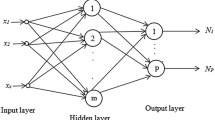
This paper presents a function approximation to a general class of polynomials by using one-hidden-layer feedforward neural networks(FNNs). Both the approximations of algebraic polynomial and trigonometric polynomial functions are discussed in details. For algebraic polynomial functions, an one-hidden-layer FNN with chosen number of hidden-layer nodes and corresponding weights is established by a constructive method to approximate the polynomials to a remarkable high degree of accuracy. For trigonometric functions, an upper bound of approximation is therefore derived by the constructive FNNs. In addition, algorithmic examples are also included to confirm the accuracy performance of the constructive FNNs method. The results show that it improves efficiently the approximations of both algebraic polynomials and trigonometric polynomials. Consequently, the work is really of both theoretical and practical significance in constructing a one-hidden-layer FNNs for approximating the class of polynomials. The work also paves potentially the way for extending the neural networks to approximate a general class of complicated functions both in theory and practice.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Cybenko G (1989) Approximation by superpositions of a sigmoid function. Math Contr Signals Syst 2:303–314

    Article  MathSciNet  MATH  Google Scholar 

  2. Hornik K, Stinchombe M, White H (1989) Multilayer feedforward networks are universal approximator. Neural Netw 2:359–366

    Article  Google Scholar 

  3. Hornik K (1993) Some new results on neural network approximation. Neural Netw 6:1069–1072

    Article  Google Scholar 

  4. Kůrkova V, Kainen PC, Kreinovich V (1997) Estimates for the number of hidden units and variation with respect to half-space. Neural Netw 10:1068–1078

    Google Scholar 

  5. Leshno M, Lin VY, Pinks A, Schocken S (1993) Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Netw 6:861–867

    Article  Google Scholar 

  6. Attali JG, Pages G (1997) Approximation of functions by a multilayer perceptron: a new approach. Neural Netw 10:1069–1081

    Article  Google Scholar 

  7. Chui CK, Li X (1992) Approximation by ridge functions and neural networks with one hidden layer. J Approx Theory 70:131–141

    Article  MathSciNet  MATH  Google Scholar 

  8. Hornik K, Stinchcombe M, White H, Auer P (1994) Degree of approximation results for feedforward networks approximating unknown mappings and theirs derivatives. Neural Comput 6:1262–1275

    Article  MATH  Google Scholar 

  9. Chen TP, Chen H (1995) Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to a dynamic system. IEEE Trans Neural Netw 6:911–917

    Article  Google Scholar 

  10. Chen TP (1994) Approximation problems in system identification with neural networks. Sci China Ser A 24(1):1–7

    Google Scholar 

  11. Yoshifusa I (1991) Approximation of functions on a compact set by finite sums of sigmoid function without scaling. Neural Netw 4:817–826

    Article  Google Scholar 

  12. Chen XH, White H (1999) Improved rates and asymptotic normality for nonparametric neural network estimators. IEEE Trans Inform Theory 45:682–691

    Article  MathSciNet  MATH  Google Scholar 

  13. Gallant AR, White H (1992) On learning the derivatives of an unknown mapping with multilayer feedforward networks. Neural Netw 5:129–138

    Article  Google Scholar 

  14. Cao FL, Xu ZB, Liang JY (2003) Approximation of ploynomial functions by neural networks: construction of network and algorithm of approximation. Chin J Comput 26(8):906–912 (in Chinese)

    MathSciNet  Google Scholar 

  15. Xu ZB, Cao FL (2005) Simultaneous L p-approximation order for neural networks. Neural Netw 18:914–923

    Article  MathSciNet  MATH  Google Scholar 

  16. Timan AF (1963) Theory of approximation of functions of a real variable. Macmillan, New York

    MATH  Google Scholar 

  17. Suzuki S (1998) Constructive function approximation by three-layer artificial neural networks. Neural Netw 11:1049–1058

    Article  Google Scholar 

Download references

Acknowledgement

This work was supported by Natural Science Foundation of China (NOs.11001227, 60972155),the Key Project of Chinese Ministry of Education (No.108176), Natural Science Foundation Project of CQ CSTC(No.CSTC, 2009BB2306, CSTC2009BB2305), the Fundamental Research Funds for the Central Universities(No.XDJK2010B005, XDJK2010C023).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Southwest University, Chongqing, 400715, People’s Republic of China

    Jian-Jun Wang

  2. Institute for Information and System Science, Xi’an Jiaotong University, Xi’an, 710049, People’s Republic of China

    Jian-Jun Wang & Bai-Li Chen

  3. Department of Mechanical Engineering, Technology and Science Institute of Northern Taiwan, No. 2 Xue-Yuan Rd, Beitou, Taipei, 112, Taiwan

    Chan-Yun Yang

Authors
  1. Jian-Jun Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Bai-Li Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Chan-Yun Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jian-Jun Wang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, JJ., Chen, BL. & Yang, CY. Approximation of algebraic and trigonometric polynomials by feedforward neural networks. Neural Comput & Applic 21, 73–80 (2012). https://doi.org/10.1007/s00521-011-0617-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-011-0617-3

Keywords