Skip to main content

Advertisement

Springer Nature Link
Log in

Superior robustness of power-sum activation functions in Zhang neural networks for time-varying quadratic programs perturbed with large implementation errors

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

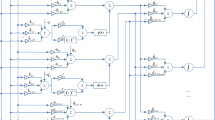
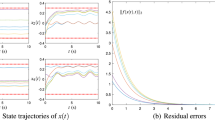
A special class of recurrent neural network termed Zhang neural network (ZNN) depicted in the implicit dynamics has recently been introduced for online solution of time-varying convex quadratic programming (QP) problems. Global exponential convergence of such a ZNN model is achieved theoretically in an error-free situation. This paper investigates the performance analysis of the perturbed ZNN model using a special type of activation functions (namely, power-sum activation functions) when solving the time-varying QP problems. Robustness analysis and simulation results demonstrate the superior characteristics of using power-sum activation functions in the context of large ZNN-implementation errors, compared with the case of using linear activation functions. Furthermore, the application to inverse kinematic control of a redundant robot arm also verifies the feasibility and effectiveness of the ZNN model for time-varying QP problems solving.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Boyd S, Vandenberghe L (2004) Convex optimization. Cambridge University Press, New York

    MATH  Google Scholar 

  2. Li W (1995) Error bounds for piecewise convex quadratic programs and applications. SIAM J Control Optim 33:1510–1529

    Article  MathSciNet  MATH  Google Scholar 

  3. Johansen TA, Fossen TI, Berge SP (2004) Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming. IEEE Trans Control Syst Technol 12:211–216

    Article  Google Scholar 

  4. Fares B, Noll D, Apkarian P (2002) Robust control via sequential semidefinite programming. SIAM J Control Optim 40:1791–1820

    Article  MathSciNet  MATH  Google Scholar 

  5. Grudinin N (1998) Reactive power optimization using successive quadratic programming method. IEEE Trans Power Syst 13:1219–1225

    Article  Google Scholar 

  6. Wang J, Zhang Y (2004) Recurrent neural networks for real-time computation of inverse kinematics of redundant manipulators. Machine intelligence quo vadis? World Scientific, Singapore

    Google Scholar 

  7. Zhang Y, Tan Z, Chen K, Yang Z, Lv X (2009) Repetitive motion of redundant robots planned by three kinds of recurrent neural networks and illustrated with a four-link planar manipulator’s straight-line example. Rob Auton Syst 57:645–651

    Article  Google Scholar 

  8. Zhang Y, Ma W, Li X, Tan H, Chen K (2009) MATLAB Simulink modeling and simulation of LVI-based primal-dual neural network for solving linear and quadratic programs. Neurocomputing 72:1679–1687

    Article  Google Scholar 

  9. Leithead WE, Zhang Y (2007) O(N 2)-operation approximation of covariance matrix inverse in Gaussian process regression based on quasi-Newton BFGS method. Commun Stat Simul Comput 36:367–380

    Article  MathSciNet  MATH  Google Scholar 

  10. Leibfritz F, Sachs EW (1999) Inexact SQP interior point methods and large scale optimal control problems. SIAM J Control Optim 38:272–293

    Article  MathSciNet  MATH  Google Scholar 

  11. Boggs PT, Tolle JW (1995) Sequential quadratic programming. Acta Numer 4:1–51

    Article  MathSciNet  Google Scholar 

  12. Murray W (1997) Sequential quadratic programming methods for large-scale problems. Comput Optim Appl 7:127–142

    Article  MathSciNet  MATH  Google Scholar 

  13. Hu J, Wu Z, McCann H, Davis LE, Xie C (2005) Sequential quadratic programming method for solution of electromagnetic inverse problems. IEEE Trans Antennas Propag 53:2680–2687

    Article  MathSciNet  Google Scholar 

  14. Chua LO, Lin G (1984) Nonlinear programming without computation. IEEE Trans Circuits Syst 31:182–188

    Article  MathSciNet  Google Scholar 

  15. Kennedy MP, Chua LO (1988) Neural networks for nonlinear programming. IEEE Trans Circuits Syst 35:554–562

    Article  MathSciNet  Google Scholar 

  16. Benson M, Carrasco RA (2001) Application of a recurrent neural network to space diversity in SDMA and CDMA mobile communication systems. Neural Comput Appl 10:136–147

    Article  MATH  Google Scholar 

  17. Suemitsu Y, Nara S (2003) A note on time delayed effect in a recurrent neural network model. Neural Comput Appl 11:137–143

    Article  MATH  Google Scholar 

  18. Zhang Y, Ma W, Cai B (2009) From Zhang neural network to Newton iteration for matrix inversion. IEEE Trans Circuits Syst I 56(7):1405–1415

    Article  MathSciNet  Google Scholar 

  19. Zhang Y, Ge SS (2005) Design and analysis of a general recurrent neural network model for time-varying matrix inversion. IEEE Trans Neural Netw 16(6):1477–1490

    Article  Google Scholar 

  20. Zhang Y, Jiang D, Wang J (2002) A recurrent neural network for solving Sylvester equation with time-varying coefficients. IEEE Trans Neural Netw 13(5):1053–1063

    Article  Google Scholar 

  21. Li Z, Zhang Y (2010) Improved Zhang neural network model and its solution of time-varying generalized linear matrix equations. Expert Syst Appl 37((10):7213–7218

    Article  Google Scholar 

  22. Zhang Y, Li Z (2009) Zhang neural network for online solution of time-varying convex quadratic program subject to time-varying linear-equality constraints. Phys Lett A 373:1639–1643

    Article  MATH  Google Scholar 

  23. Myung H, Kim J (1997) Time-varying two-phase optimization and its application to neural-network learning. IEEE Trans Neural Netw 8:1293–1300

    Article  Google Scholar 

  24. Mead C (1989) Analog VLSI and neural systems. Addison-Wesley, Reading

    Book  MATH  Google Scholar 

Download references

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grants 61075121 and 60935001, and also by the Fundamental Research Funds for the Central Universities of China. In addition, the authors would like to thank the editors and anonymous reviewers sincerely for their constructive comments and suggestions which have really improved the presentation and quality of this paper very much.

Author information

Authors and Affiliations

  1. School of Information Science and Technology, Sun Yat-sen University, Guangzhou, 510006, China

    Yiwen Yang & Yunong Zhang

Authors
  1. Yiwen Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yunong Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yunong Zhang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yang, Y., Zhang, Y. Superior robustness of power-sum activation functions in Zhang neural networks for time-varying quadratic programs perturbed with large implementation errors. Neural Comput & Applic 22, 175–185 (2013). https://doi.org/10.1007/s00521-011-0692-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-011-0692-5

Keywords