Skip to main content

Advertisement

Springer Nature Link
Log in

New conditions for global exponential stability of continuous-time neural networks with delays

  • Cont. Dev. of Neural Compt. & Appln.
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

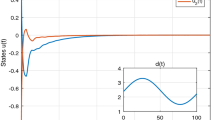
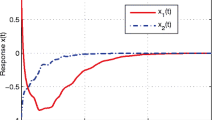
In this paper, we investigate the global exponential stability of delayed neural network systems. For this purpose, the activation functions are assumed to be globally Lipschitz continuous. The properties of norms and the relationship of homeomorphism are adjusted to ensure the existence as well as the uniqueness of the equilibrium point. Then by employing suitable Lyapunov functional, some delay-independent sufficient conditions are derived for exponential convergence toward global equilibrium state associated with different input sources. The obtained results are shown to be more general and less restrictive than the previous results derived in the literature. Lastly, a number of examples are provided to demonstrate the validity of the results proposed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Abarbanel H (1996) Analysis of observed chaotic data. Springer, New York

    Book  MATH  Google Scholar 

  2. Arik S (2000) Global asymptotic stability of a class of dynamical neural networks. IEEE Trans Circuits Syst I 47:568–571

    Article  MathSciNet  MATH  Google Scholar 

  3. Arik S (2002) An improved global stability result for delayed cellular neural networks. IEEE Trans Circuits Syst I 49:1211–1214

    Article  MathSciNet  Google Scholar 

  4. Arik S (2004) An analysis of exponential stability of delayed neural networks with time varying delays. Neural Netw 17:1027–1031

    Article  MATH  Google Scholar 

  5. Bergh F, Engelbrecht A (2006) A study of particle swarm optimization particle trajectories. Inf Sci 176:937–971

    Article  MATH  Google Scholar 

  6. Bisler A (2004) An associative memory for autonomous agents. In: Proceedings of 4th international conference on intelligent systems design and applications, pp 765–770

  7. Cai Z (2004) Intelligent control, vol II. Publish House of Electronic Industry

  8. Campana E, Fasano G, Pinto A (2006) Dynamic system analysis and initial particles position in particle swarm optimization. In: Proceedings of the IEEE swarm intelligence symposium, pp 202–209

  9. Cao J (2001) Global stability conditions for delayed CNNs. IEEE Trans Circuits Syst I 48:1330–1333

    Article  MATH  Google Scholar 

  10. Cao J, Song Q (2006) Stability in Cohen-Grossberg type BAM neural networks. Nonlinearity 19(7):1601–1617

    Article  MathSciNet  MATH  Google Scholar 

  11. Cao J, Wang J (2003) Global asymptotic stability of a general class of recurrent neural networks with time—varying delays. IEEE Trans Circuits Syst I 50:34–44

    Article  MathSciNet  Google Scholar 

  12. Cao J, Wang J (2005) Global exponential stability and periodicity of recurrent neural networks with time delays. IEEE Trans Circuits Syst I 920–931

  13. Chu T, Zhang C (2007) New necessary and sufficient conditions for absolute stability of neural networks. Neural Netw 20:94–101

    Article  MATH  Google Scholar 

  14. Chu T, Zhang C, Zhang Z (2003) Necessary and sufficient condition for absolute stability of normal neural networks. Neural Netw 16:1223–1227

    Article  Google Scholar 

  15. Forti M, Tesi A (1995) New conditions for global stability of neural networks with application to linear and quadratic programming problems. IEEE Trans Circuits Syst I 42:354–365

    Article  MathSciNet  MATH  Google Scholar 

  16. Ge SS (2001) Stable adaptive neural network control. Kluwer, Norwell

    Google Scholar 

  17. He Y, Wang Q, Wu M, Lin C (2006) Delay-dependent state estimation for delayed neural networks. IEEE Trans Neural Netw 17:1077–1081

    Article  MATH  Google Scholar 

  18. Hu S, Wang J (2002) Global exponential stability of continuous-time interval neural networks. IEEE Trans Circuits Syst I 49:1334–1347

    Article  Google Scholar 

  19. Huang H, Teng Z (2005) A new criterion on global exponential stability for cellular neural networks with multiple time-varying delays. Phys Lett A 338:461–471

    Article  Google Scholar 

  20. Inoue T, Abe S (2001) Fuzzy support vector machines for pattern classification. In: Proceedings of the international joint conference on neural networks (IJCNN’01), vol 2, Jul, pp 15–19

  21. Khalil H (1998) Nonlinear systems. Macmillan, New York

    Google Scholar 

  22. Li Z (2008) Adaptive neural-fuzzy control of uncertain constrained multiple coordinated nonholonomic mobile manipulators. Eng Appl Artif Intell 21(7):985–1000

    Article  Google Scholar 

  23. Li X, Huang L, Zhu H (2003) Global stability of cellular neural networks with constant and variable delays. Nonlinear Anal 53:319–333

    Article  MathSciNet  MATH  Google Scholar 

  24. Li Z, Gu J, Ming A, Xu C, Shimojo M (2006) Intelligent complaint force/motion control of nonholonomic mobile manipulator working on the non-rigid surface. Neural Comput Appl 15(3–4):204–216

    Google Scholar 

  25. Liao X, Chen G (2002) LMI-based approach for asymptotically stability analysis of delayed neural networks. IEEE Trans Circuits Syst I 49:1033–1039

    Article  MathSciNet  Google Scholar 

  26. Lu W, Rong L, Chen T (2003) Global convergence of delayed dynamical systems [J]. Int J Neural Syst I 13:1–12

    Article  Google Scholar 

  27. Mohamad S, Gopalsamy K (2003) Exponential stability of continuous-time and discrete-time cellular neural networks. Appl Math Comput 135:17–38

    Article  MathSciNet  MATH  Google Scholar 

  28. Rhodes B (2000) Margin notes: Building a contextually aware associative memory. In: Proceedings of the international conference on intelligent user interfaces, pp 9–12

  29. Singh V (2007) Improved global robust stability criterion for delayed neural networks. Chaos Solitons Fractals 31:224–229

    Article  MathSciNet  MATH  Google Scholar 

  30. Song Q (2008) Exponential stability of recurrent neural networks with both time-varying delays and general activation functions via LMI approach. Neurocomputing 71:2823–2830

    Article  Google Scholar 

  31. Wang J, Lee C (2002) Self-Adaptive neuro-fuzzy inference systems for classification applications. IEEE Trans Fuzzy Syst 10(6):790–802

    Article  Google Scholar 

  32. Wu H (2008) Global exponential stability of Hopfield neural networks with delays and inverse Lipschitz neuron activations. Nonlinear Anal Real World Appl. doi:10.1016/j.nonrwa. 04.016

  33. Xu S, Lam J (2006) A new approach to exponential stability analysis of neural networks with time-varying delays. Neural Netw 19:76–83

    Article  MATH  Google Scholar 

  34. Xu S, Chu Y, Lu J (2006) New results on global exponential stability of recurrent neural networks with time-varying delays. Phys Lett A 352(4–5):371–379

    Article  MATH  Google Scholar 

  35. Yucel E, Arik S (2007) Novel result for global robust stability of delayed neural networks. Sci Direct 06:052

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin, 150001, China

    Haibo Gao, Xingguo Song, Liang Ding & Minghui Hao

  2. Yanshan University, Qinhuangdao, 066004, China

    Deyou Liu

Authors
  1. Haibo Gao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xingguo Song
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Liang Ding
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Deyou Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Minghui Hao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xingguo Song.

Additional information

This work was supported by the National Natural Science Foundation of China (50975059/61005080), China Postdoctoral Special Science Foundation (201104405), China Postdoctoral Science Foundation (20100480994), and the “111” Project (B07018).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gao, H., Song, X., Ding, L. et al. New conditions for global exponential stability of continuous-time neural networks with delays. Neural Comput & Applic 22, 41–48 (2013). https://doi.org/10.1007/s00521-011-0745-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-011-0745-9

Keywords