Skip to main content
Springer Nature Link
Log in

Hyperchaos synchronization using PSO-optimized RBF-based controllers to improve security of communication systems

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

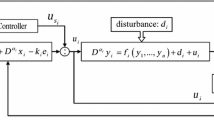
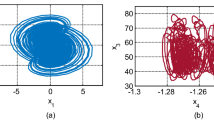
Abstract

This paper studies the Lorenz hyperchaos synchronization and its application to improve the security of communication systems. Two methods are proposed to synchronize the general forms of hyperchaotic systems, and their performance in secure communication application is verified. These methods use the radial basis function (RBF)-based neural controllers for this purpose. The first method uses a standard RBF neural controller. Particle swarm optimization (PSO) algorithm is used to derive and optimize the parameters of the RBF controller. In the second method, with the aim of increasing the robustness of the RBF controller, an error integral term is added to the equations of RBF neural network. For this method, the coefficients of the error integral component and the parameters of RBF neural network are also derived and optimized via PSO algorithm. For better comparison, the proposed methods and an optimal PID controller optimized by PSO are applied to the Lorenz hyperchaotic system for secure communication. Simulation results show the effectiveness and superiority of the proposed methods in both performance and robustness in comparison with the PID controller.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Yang T, Chua LO (1997) Impulsive stabilization for control and synchronization of chaotic systems: theory and application to secure communication. IEEE Trans Circuits Syst I Fundam Theory Appl 44:976–988

    Article  MathSciNet  Google Scholar 

  2. Chee CY, Xu D (2005) Secure digital communication using controlled projective synchronization of chaos. Chaos Solitons Fractals 23:1063–1070

    MATH  Google Scholar 

  3. Bai EW, Lonngren KE, Uçar A (2005) Secure communication via multiple parameter modulation in a delayed chaotic system. Chaos Solitons Fractals 23:1071–1076

    MATH  Google Scholar 

  4. Li C, Liao X, Wong K (2005) Lag synchronization of hyperchaos with application to secure communications. Chaos Solitons Fractals 23:183–193

    Article  MathSciNet  MATH  Google Scholar 

  5. Hyun C-H, Kim J-H, Kim E, Park M (2006) Adaptive fuzzy observer based synchronization design and secure communications of chaotic systems. Chaos Solitons Fractals 27:930–940

    Article  MathSciNet  MATH  Google Scholar 

  6. Chen HC, Chang JF, Yan JJ, Liao TL (2008) EP-based PID control design for chaotic synchronization with application in secure communication. Expert Syst Appl 34:1169–1177

    Article  Google Scholar 

  7. Changchien S-K, Huang C-K, Nien H-H, Shieh H-W (2009) Synchronization of the chaotic secure communication system with output state delay. Chaos Solitons Fractals 39:1578–1587

    Article  MathSciNet  MATH  Google Scholar 

  8. Hyun C-H, Park C-W, Kim J-H, Park M (2009) Synchronization and secure communication of chaotic systems via robust adaptive high-gain fuzzy observer. Chaos Solitons Fractals 40:2200–2209

    Article  MathSciNet  MATH  Google Scholar 

  9. Chang W-D (2009) Digital secure communication via chaotic systems. Digit Signal Process 19:693–699

    Article  Google Scholar 

  10. Wang XY, Wang M-J (2009) A chaotic secure communication scheme based on observer. Commun Nonlinear Sci Numer Simulat 14:1502–1508

    Article  Google Scholar 

  11. Zhu F (2009) Observer-based synchronization of uncertain chaotic system and its application to secure communications. Chaos Solitons Fractals 40:2384–2391

    Article  MATH  Google Scholar 

  12. Grzybowski JMV, Rafikov M, Balthazar JM (2009) Synchronization of the unified chaotic system and application in secure communication. Commun Nonlinear Sci Numer Simul 14:2793–2806

    Article  MathSciNet  MATH  Google Scholar 

  13. Lin J-S, Huang C-F, Liao T-L, Yan J-J (2010) Design and implementation of digital secure communication based on synchronized chaotic systems. Digit Signal Process 20:229–237

    Article  Google Scholar 

  14. Wang F, Liu C (2007) Synchronization of unified chaotic system based on passive control. Physica D 225:55–60

    Article  MathSciNet  MATH  Google Scholar 

  15. Zhang H, Ma X (2004) Synchronization of uncertain chaotic systems with parameters perturbation via active control. Chaos Solitons Fractals 21:39–47

    Article  MathSciNet  MATH  Google Scholar 

  16. Lin J-S, Yan J-J (2009) Adaptive synchronization for two identical generalized Lorenz chaotic systems via a single controller. Nonlinear Anal Real World Appl 10:1151–1159

    Article  MathSciNet  MATH  Google Scholar 

  17. Salarieh H, Alasti A (2009) Adaptive synchronization of two chaotic systems with stochastic unknown parameters. Commun Nonlinear Sci Numer Simul 14:508–519

    Article  MathSciNet  MATH  Google Scholar 

  18. Yau H-T, Shieh C-S (2008) Chaos synchronization using fuzzy logic controller. Nonlinear Anal Real World Appl 9:1800–1810

    Article  MathSciNet  MATH  Google Scholar 

  19. Li S-Y, Ge Z-M (2011) Generalized synchronization of chaotic systems with different orders by fuzzy logic constant controller. Expert Syst Appl 38:2302–2310

    Article  Google Scholar 

  20. Morgül Ö, Akgül M (2002) A switching synchronization scheme for a class of chaotic systems. Phys Lett A 301:241–249

    Article  MathSciNet  MATH  Google Scholar 

  21. Jiang GP, Chen GR, Tang WK (2003) A new criterion for chaos synchronization using linear state feedback control. Int J Bifurc Chaos 13:2343–2351

    Article  MATH  Google Scholar 

  22. Lin D, Wang X, Nian F, Zhang Y (2010) Dynamic fuzzy neural networks modeling and adaptive backstepping tracking control of uncertain chaotic systems. Neurocomputing 73:2873–2881

    Article  Google Scholar 

  23. Wang H, Han ZZ, Xie QY, Zhang W (2009) Finite-time chaos control via nonsingular terminal sliding mode control. Commun Nonlinear Sci Numer Simulat 14:2728–2733

    Article  MathSciNet  MATH  Google Scholar 

  24. Mou C, Jiang C-S, Bin J, Wu Q-X (2009) Sliding mode synchronization controller design with neural network for uncertain chaotic systems. Chaos Solitons Fractals 39:1856–1863

    Article  MATH  Google Scholar 

  25. Pourmahmood M, Khanmohammadi S, Alizadeh G (2011) Synchronization of two different uncertain chaotic systems with unknown parameters using a robust adaptive sliding mode controller. Commun Nonlinear Sci Numer Simulat 16:2853–2868

    Article  MathSciNet  MATH  Google Scholar 

  26. Lin T-C, Chen M-C, Roopaei M (2011) Synchronization of uncertain chaotic systems based on adaptive type-2 fuzzy sliding mode control. Eng Appl Artif Intell 24:39–49

    Article  Google Scholar 

  27. Zheng Y, Chen G (2009) Fuzzy impulsive control of chaotic systems based on TS fuzzy model. Chaos Solitons Fractals 39:2002–2011

    Article  MathSciNet  MATH  Google Scholar 

  28. Yin C, Zhong S-M, Chen W-F (2011) Design PD controller for master-slave synchronization of chaotic Lur’e systems with sector and slope restricted nonlinearities. Commun Nonlinear Sci Numer Simulat 16:1632–1639

    Article  MathSciNet  MATH  Google Scholar 

  29. Coelho LS, Bernert DLA (2009) PID control design for chaotic synchronization using a Tribes optimization approach. Chaos Solitons Fractals 42:634–640

    Article  Google Scholar 

  30. Coelho LS, Grebogi RB (2010) Chaotic synchronization using PID control combined with population based incremental learning algorithm. Expert Syst Appl 37:5347–5352

    Article  Google Scholar 

  31. Coelho LS, Bernert DLA (2010) A modified ant colony optimization algorithm based on differential evolution for chaotic synchronization. Expert Syst Appl 37:4198–4203

    Article  Google Scholar 

  32. Ren H, Liu D (2007) Synchronization of chaos using radial basis functions neural networks. J Syst Eng Electron 18:83–88

    Article  Google Scholar 

  33. Hsu C-F, Chung C-M, Lin C-M, Hsu C-Y (2009) Adaptive CMAC neural control of chaotic systems with a PI-type learning algorithm. Expert Syst Appl 36:11836–11843

    Article  Google Scholar 

  34. Chen M, Chen W (2009) Robust adaptive neural network synchronization controller design for a class of time delay uncertain chaotic systems. Chaos Solitons Fractals 41:2716–2724

    Article  MATH  Google Scholar 

  35. Sheikhan M, Shahnazi R, Garoucy S (2011) Synchronization of general chaotic systems using neural controllers with application to secure communication. Neural Comput Appl (article in press). doi:10.1007/s00521-011-0697-0

  36. Chen C-S, Chen H-H (2009) Robust adaptive neural-fuzzy-network control for the synchronization of uncertain chaotic systems. Nonlinear Anal Real World Appl 10:1466–1479

    Article  MathSciNet  MATH  Google Scholar 

  37. Chen C-S (2009) Quadratic optimal neural fuzzy control for synchronization of uncertain chaotic systems. Expert Syst Appl 36:11827–11835

    Article  Google Scholar 

  38. Lin D, Wang X (2011) Self-organizing adaptive fuzzy neural control for the synchronization of uncertain chaotic systems with random-varying parameters. Neurocomputing 74:2241–2249

    Article  Google Scholar 

  39. Kolumbán G, Kennedy MP, Chua LO (1997) The role of synchronization in digital communication using chaos I. Fundamentals of digital communications. IEEE Trans Circuits Syst I Fundam Theory Appl 44:927–936

    Article  Google Scholar 

  40. Wu X-J, Wang H, Lu H-T (2011) Hyperchaotic secure communication via generalized function projective synchronization. Nonlinear Anal Real World Appl 12:1288–1299

    Article  MathSciNet  MATH  Google Scholar 

  41. Rössler OE (1976) An equation for continuous chaos. Phys Lett A 57:397–398

    Article  Google Scholar 

  42. Kapitaniak T, Steeb WH (1991) Transition to hyperchaos in coupled generalized Van der Pol equations. Phys Lett A 152:33–36

    Article  MathSciNet  Google Scholar 

  43. Anishchenko VS, Kapitaniak T, Safonova MA, Sosnovzeva OV (1994) Birth of double–double scroll attractor in coupled Chua circuit. Phys Lett A 192:207–214

    Article  MathSciNet  MATH  Google Scholar 

  44. Kapitaniak T, Chua LO, Zhung GQ (1994) Experimental hyperchaos in coupled Chua’s circuits. IEEE Trans Circuits Syst I Fundam Theory Appl 41:499–503

    Article  Google Scholar 

  45. Hsieh JY, Hwang CC, Wang AP, Li WJ (1999) Controlling hyperchaos of the Rössler system. Int J Control 72:882–886

    Article  MathSciNet  MATH  Google Scholar 

  46. Laval L, M’Sirdi NK (2002) Controlling chaotic and hyperchaotic systems via energy regulation. Chaos Solitons Fractals 14:1015–1025

    Article  MathSciNet  MATH  Google Scholar 

  47. Jang MJ, Chen CL, Chen CK (2002) Sliding mode control of hyperchaos in Rössler systems. Chaos Solitons Fractals 14:1465–1476

    Article  MathSciNet  MATH  Google Scholar 

  48. Yau HT, Yan JJ (2007) Robust controlling hyperchaos of the Rössler system subject to input nonlinearities by using sliding mode control. Chaos Solitons Fractals 33:1767–1776

    Article  MathSciNet  MATH  Google Scholar 

  49. Wang H, Han ZZ, Mo Z (2010) Synchronization of hyperchaotic systems via linear control. Commun Nonlinear Sci Numer Simulat 15:1910–1920

    Article  MathSciNet  MATH  Google Scholar 

  50. Zheng S, Dong G, Bi Q (2010) Adaptive modified function projective synchronization of hyperchaotic systems with unknown parameters. Commun Nonlinear Sci Numer Simulat 15:3547–3556

    Article  MathSciNet  MATH  Google Scholar 

  51. An H-L, Chen Y (2009) The function cascade synchronization scheme for discrete-time hyperchaotic systems. Commun Nonlinear Sci Numer Simulat 14:1494–1501

    Article  MathSciNet  MATH  Google Scholar 

  52. Kennedy J, Eberhart RC (1995) Particle swarm optimization. In: The proceedings of the international conference on neural networks, pp 1942–1948

  53. Wang F, Liu C (2006) A new criterion and hyperchaos synchronization using linear feedback control. Phys Lett A 360:274–278

    Article  MATH  Google Scholar 

  54. Wang F, Liu C (2007) Passive control of hyperchaotic Lorenz system and circuit experimental on EWB. Int J Modern Phys B 21:3053–3064

    Article  MATH  Google Scholar 

  55. Wu X, Guan Z-H, Wu Z (2008) Adaptive synchronization between two different hyperchaotic systems. Nonlinear Anal 68:1346–1351

    Article  MathSciNet  MATH  Google Scholar 

  56. Xu J, Cai G, Zheng S (2009) Adaptive synchronization for an uncertain new hyperchaotic Lorenz system. Int J Nonlinear Sci 8:117–123

    MathSciNet  MATH  Google Scholar 

  57. Li C (2011) Tracking control and generalized projective synchronization of a class of hyperchaotic system with unknown parameter and disturbance. Commun Nonlinear Sci Numer Simulat (article in press). doi:10.1016/j.cnsns.2011.05.017

  58. Smaoui N, Karouma A, Zribi M (2011) Secure communications based on the synchronization of the hyperchaotic Chen and the unified chaotic systems. Commun Nonlinear Sci Numer Simulat 16:3279–3293

    Article  MathSciNet  MATH  Google Scholar 

  59. Li Y, Tang WKS, Chen G (2005) Generating hyperchaos via state feedback control. Int J Bifur Chaos 15:3367–3375

    Article  Google Scholar 

  60. Chen A, Lu J, Lü J, Yu S (2006) Generating hyperchaos Lü attractor via state feedback control. Phys A 364:103–110

    Article  Google Scholar 

  61. Jia Z, Lu J, Deng G (2007) Nonlinearity state feedback and adaptive synchronization of hyperchaotic Lü systems. Syst Eng Electron 29:598–600

    MATH  Google Scholar 

  62. Wang F-Q, Liu C-X (2006) Hyperchaos evolved from the Liu chaotic system. Chin Phys 15:963–968

    Article  Google Scholar 

  63. Liu C, Liu T, Liu L, Liu K (2004) A new chaotic attractor. Chaos Solitons Fractals 22:1031–1038

    Article  MathSciNet  MATH  Google Scholar 

  64. Jia Q (2007) Hyperchaos generated from the Lorenz chaotic system and its control. Phys Lett A 366:217–222

    Article  MATH  Google Scholar 

  65. Khadra A, Liu ZX, Shen X (2005) Impulsively synchronizing chaotic systems with delay and applications to secure communication. Automatica 41:1491–1502

    Article  MathSciNet  MATH  Google Scholar 

  66. Grassi G (2009) Observer-based hyperchaos synchronization in cascaded discrete-time systems. Chaos Solitons Fractals 40:1029–1039

    Article  MathSciNet  MATH  Google Scholar 

  67. Hu M, Xu Z, Zhang R (2008) Full state hybrid projective synchronization in continuous-time chaotic (hyperchaotic) systems. Commun Nonlinear Sci Numer Simulat 13:456–464

    Article  MathSciNet  MATH  Google Scholar 

  68. Zhu C (2010) Control and synchronize a novel hyperchaotic system. Appl Math Comput 216:274–284

    Google Scholar 

  69. Shi Y, Eberhart RC (1998) Parameter selection in particle swarm optimization. In: The proceedings of the international conference on evolutionary programming, pp 591–600

  70. Chen S, Billings SA, Cowan CFN, Grant PW (1990) Practical identification of Narmax models using radial basis functions. Int J Control 52:1327–1350

    Article  MathSciNet  MATH  Google Scholar 

  71. Holcomb T, Moran M (1991) Local training for radial basis function networks: towards solving the hidden unit problem. In: The proceedings of the American control conference, pp 2331–2336

  72. Lee S, Rhce MK (1991) A Gaussian potential function network with hierarchically self-organizing learning. Neural Netw 4:207–224

    Article  Google Scholar 

  73. Musavi MT, Ahmed W, Chan KH, Faris KB, Hummels DM (1992) On the training of radial basis function classifiers. Neural Netw 5:595–603

    Article  Google Scholar 

  74. Lan Y, Soh YC, Huang G-B (2010) Constructive hidden nodes selection of extreme learning machine for regression. Neurocomputing 73:3191–3199

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, Islamic Azad University, South Tehran Branch, P.O. Box 11365-4435, Tehran, Iran

    Mansour Sheikhan & Sahar Garoucy

  2. Modeling and Optimization Research Center in Science and Engineering, Islamic Azad University, South Tehran Branch, Tehran, Iran

    Reza Shahnazi

Authors
  1. Mansour Sheikhan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Reza Shahnazi
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Sahar Garoucy
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mansour Sheikhan.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Sheikhan, M., Shahnazi, R. & Garoucy, S. Hyperchaos synchronization using PSO-optimized RBF-based controllers to improve security of communication systems. Neural Comput & Applic 22, 835–846 (2013). https://doi.org/10.1007/s00521-011-0774-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-011-0774-4

Keywords