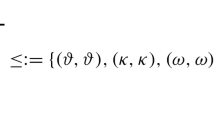Abstract
In Jun et al. (Bull Malays Math Sci Soc (2) 32(3):391–408, 2009), (α, β)-fuzzy bi-ideals are introduced and some characterizations are given. In this paper, we generalize the concept of (α, β)-fuzzy bi-ideals and define (\(\in ,\in \vee q_{k}\))-fuzzy bi-ideals in ordered semigroups, which is a generalization of the concept of an (α, β)-fuzzy bi-ideal in an ordered semigroup. Using this concept, some characterization theorems of regular, left (resp. right) regular and completely regular ordered semigroups are provided. In the last section, we give the concept of upper/lower parts of an (\(\in ,\in \vee q_{k}\))-fuzzy bi-ideal and investigate some interesting results of regular and intra-regular ordered semigroups.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Bhakat SK, Das P (1996) \(\left( \in ,\in \vee q\right) \)-fuzzy subgroups. Fuzzy Sets Syst 80:359–368
Bhakat SK, Das P (1996) Fuzzy subrings and ideals redefined. Fuzzy Sets Syst 81:383–393
Davvaz B, Khan A (2011) Characterizations of regular ordered semigroups in terms of \(\left( \alpha ,\beta \right) \)-fuzzy generalized bi-ideals. Inform Sci 181:1759–1770
Davvaz B (2008) Fuzzy R-subgroups with thresholds of near-rings and implication operators. Soft Comput 12:875–879
Davvaz B (2006) (\(\in ,\in \vee \)q)-fuzzy subnear-rings and ideals. Soft Comput 10:206–211
Jun YB, Khan A, Shabir M (2009) Ordered semigroups characterized by their (\(\in ,\in \vee \)q)-fuzzy bi-ideals. Bull Malays Math Sci Soc (2) 32(3):391–408
Jun YB (2005) On (α, β)-fuzzy subalgebras of BCK/BCI-algebras. Bull Korean Math Soc 42(4):703–711
Jun YB (2009) Generalizations of (\(\in ,\in \vee \)q)-fuzzy subalgebras in BCK/BCI-algebras. Comput Math Appl 58:1383–1390
Jun YB, Dudek WA, Shabir M, Kang MS (2010) General form of (α, β)-fuzzy ideals of Hemirings. Honam Math J 32(3):413–439
Khan A, Davvaz B, Sarmin NH, Khan FM Ordered semigroups characterized by (\(\in ,\in \vee q_{k}\))-fuzzy generalized bi-ideals. Neural Comput Appl. doi:10.1007/s00521-011-0731-2
Kehayopulu N, Tsingelis M (2005) Fuzzy bi-ideals in ordered semigroups. Inf Sci 171:13–28
Khan A, Jun YB, Abbasi Z Characterizations of ordered semigroups in terms of (\(\in ,\in \vee \)q)-fuzzy interior ideals. Neural Comput Appl. doi:10.1007/s00521-010-0463-8
Kuroki N (1981) On fuzzy ideals and fuzzy bi-ideals in semigroups. Fuzzy Sets Syst 5:203–215
Mordeson JN, Malik DS, Kuroki N (2003) Fuzzy semigroups. Studies in fuzziness and soft computing, vol 131. Springer, Berlin
Murali V (2004) Fuzzy points of equivalent fuzzy subsets. Inf Sci 158:277–288
Pu PM, Liu YM (1980) Fuzzy topology I, neighborhood structure of a fuzzy point and Moore-Smith convergence. J Math Anal Appl 76:571–599
Rosenfeld A (1971) Fuzzy groups. J Math Anal Appl 35:512–517
Shabir M, Jun YB, Nawaz Y (2010) Characterization of regular semigroups by \(\left( \alpha ,\beta \right) \)-fuzzy ideals. Comput Math Appl 59:161–175
Shabir M, Jun YB, Nawaz Y (2010) Semigroups characterized by (\(\in ,\in \vee q_{k}\))-fuzzy ideals. Comput Math Appl 60:1473–1493
Shabir M, Mahmood T (2011) Characterizations of hemirings by (\(\in ,\in \vee q_{k}\))-fuzzy ideals. Comput Math Appl 61:1059–1078
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Acknowledgments
We express our thanks to the referees for their valuable remarks and suggestions for the improvement of our paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Khan, A., Sarmin, N.H., Davvaz, B. et al. New types of fuzzy bi-ideals in ordered semigroups. Neural Comput & Applic 21 (Suppl 1), 295–305 (2012). https://doi.org/10.1007/s00521-012-0843-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-012-0843-3