Skip to main content
Springer Nature Link
Log in

Asymptotic stability criteria for T-S fuzzy neural networks with discrete interval and distributed time-varying delays

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

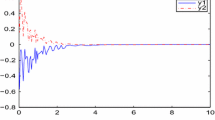
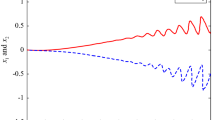
The aim of this paper is to study the problem of asymptotic stability analysis for T-S fuzzy neural networks with discrete interval and distributed time-varying delays by employing a further improved free-weighting matrix approach. Based on the new Lyapunov–Krasovskii functional with triple-integral term, using some integral inequality and convex combination technique, a new delay-dependent stability criteria are obtained in terms of linear matrix inequalities (LMIs) that can be checked easily by the LMI Control Toolbox in MATLAB. Finally, numerical examples are given to illustrate the strength of the proposed method and an improvement over some existing results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Haykin S (1998) Neural networks: a comprehensive foundation. Prentice Hall, New Jercy

    Google Scholar 

  2. Arik S (2000) Stability analysis of delayed neural networks. IEEE Trans Circuits Syst I 47:1089–1092

    Article  MathSciNet  MATH  Google Scholar 

  3. Qiu J, Yang H, Zhang J, Gao Z (2009) New robust stability criteria for uncertain neural networks with interval time-varying delays. Chaos Solitons Fractals 39:579–585

    Article  MathSciNet  MATH  Google Scholar 

  4. Kwon OM, Park JH, Lee SM (2008) On robust stability for uncertain neural networks with interval time-varying delays. IET Control Theory Appl 2:625–634

    Article  MathSciNet  Google Scholar 

  5. Hua CC, Long CN, Guan XP (2006) New results on stability analysis of neural networks with time-varying delays. Phys Lett A 352:335–340

    Article  MATH  Google Scholar 

  6. Liu HL, Chen GH (2007) Delay-dependent stability for neural networks with time-varying delay. Chaos Solitons Fractals 33:171–177

    Article  MathSciNet  MATH  Google Scholar 

  7. He Y, Liu GP, Rees D (2007) New delay-dependent stability criteria for neural networks with time-varying delay. IEEE Trans Neural Netw 18:310–314

    Article  Google Scholar 

  8. He Y, Liu GP, Rees D, Wu M (2007) Stability analysis for neural networks with time-varying interval Delay. IEEE Trans Neural Netw 18:1850–1854

    Article  Google Scholar 

  9. Chen Y, Wu Y (2009) Novel delay-dependent stability criteria of neural networks with time-varying delay. Neurocomputing 72:1065–1070

    Article  Google Scholar 

  10. Rakkiyappan R, Balasubramaniam P, Lakshmanan S (2008) Robust stability results for uncertain stochastic neural networks with discrete interval and distributed time-varying delays. Phys Lett A 372:5290–5298

    Article  MathSciNet  MATH  Google Scholar 

  11. Balasubramaniam P, Lakshmanan S (2009) Delay-range dependent stability criteria for neural networks with Markovian jumping parameters. Nonlinear Anal Hybrid Syst 3:749–756

    Article  MathSciNet  MATH  Google Scholar 

  12. Rakkiyappan R, Balasubramaniam P (2010) On exponential stability results for fuzzy impulsive neural networks. Fuzzy Sets Syst 161(13):1823–1835

    Article  MathSciNet  MATH  Google Scholar 

  13. Balasubramaniam P, Vembarasan V, Rakkiyappan R (2012) Delay-dependent robust asymptotic state estimation of Takagi-Sugeno fuzzy Hopfield neural networks with mixed interval time-varying delays. Expert Syst Appl 39(1):472–481

    Article  Google Scholar 

  14. Liu H, Zhao L, Zhang Z, Ou Y (2009) Stochastic stability of markovian jumping Hopfield neural networks with constant and distributed delays. Neurocomputing 72:3669–3674

    Article  Google Scholar 

  15. Kwon OM, Park JH (2009) Improved delay dependent stability criterion for neural networks with time-varying delays. Phys Lett A 373:529–535

    Article  MathSciNet  MATH  Google Scholar 

  16. Sun J, Liu GP, Chen J, Rees D (2009) Improved stability criteria for neural networks with time-varying delay. Phys Lett A 373:342–348

    Article  MATH  Google Scholar 

  17. Wu H, Feng W, Liang X (2008) New stability criteria for uncertain neural networks with interval time-varying delays. Cogn Neurodyn 2:363–370

    Article  Google Scholar 

  18. Tian J, Zhou X (2010) Improved asymptotic stability criteria for neural networks with interval time-varying delay. Expert Syst Appl 37:7521–7525

    Article  Google Scholar 

  19. Kwon OM, Kwon JW, Kim SH (2011) New results on stability criteria for neural networks with time-varying delays. Chin Phys B 20:050505

    Article  Google Scholar 

  20. Chen J, Sun J, Liu GP, Rees D (2010) New delay dependent stability criteria for neural networks with time-varying interval delays. Phys Lett A 374:4397–4405

    Article  MathSciNet  MATH  Google Scholar 

  21. Tian J, Zhong S, Improved delay-dependent stability criterion for neural networks with time-varying delay, Appl Math Comput. doi:10.1016/j.amc.2011.05.029

  22. Mathiyalagan K, Sakthival R, Marshal Anthoni S (2011) New stability and stabilization criteria for fuzzy neural networks with various activation functions. Phys Scr 84(1):015007

    Article  Google Scholar 

  23. Sakthival R, Mathiyalagan K, Marshal Anthoni S (2011) Design of a passification controller for uncertain fuzzy Hopfield neural networks with time-varying delays. Phys Scr 84(4):045024

    Article  Google Scholar 

  24. Sakthival R, Arunkumar A, Mathiyalagan K, Marshal Anthoni S (2011) Robust passivity analysis of fuzzy Cohen-Grossberg BAM neural networks with time-varying delays. Appl Math Comput 218:3799–3809

    Article  MathSciNet  Google Scholar 

  25. Mathiyalagan K, Sakthival R, Marshal Anthoni S (2012) New robust passivity criteria for stochastic fuzzy BAM neural networks with time-varying delays. Commun Nonlinear Sci Numer Simul 17:1392–1407

    Article  MathSciNet  MATH  Google Scholar 

  26. Sakthival R, Samidurai R, Anthoni SM (2010) Asymptotic stability of stochastic delayed recurrent neural networks with impulsive effects. J Optim Theory Appl 147:583–596

    Article  MathSciNet  Google Scholar 

  27. Li C, Liao X, Zhang R (2005) Delay-dependent exponential stability analysis of bi-directional associative memory neural networks with time delay: an LMI approach. Chaos Solitons Fractals 24:1119–1134

    Article  MathSciNet  MATH  Google Scholar 

  28. Ramakrishnan K, Ray G, Robust stability criteria for uncertain neutral systems with interval time-varying delay. J Optim Theory Appl. doi:10.1007/s10957-010-9784-0

  29. Lakshmanan S, Senthilkumar T, Balasubramaniam P (2011) Improved results on robust stability of neutral systems with mixed time-varying delays and nonlinear perturbations. Appl Math Model 35:5355–5368

    Article  MathSciNet  MATH  Google Scholar 

  30. Hopfield JJ (1984) Neurons with graded response have collective computational properties like those of two-state neurons. Proc Natl Acad Sci 81:3088–3092

    Article  Google Scholar 

  31. Marcus CM, Westervelt RM (1989) Stability of analog neural networks with delay. Phys Rev A 39:347–359

    Article  MathSciNet  Google Scholar 

  32. Takagi T, Sugeno M (1985) Fuzzy identification of systems and its applications to modeling and control. IEEE Trans Syst Man Cybern 15:116–132

    MATH  Google Scholar 

  33. Liu F, Wu M, He Y, Yokoyama R (2010) New delay-dependent stability criteria for T-S fuzzy systems with time-varying delay. Fuzzy Sets Syst 161:2033–2042

    Article  MathSciNet  MATH  Google Scholar 

  34. Cao YY, Frank PM (2001) Stability analysis and synthesis of nonlinear time-delay systems via linear Takagi-Sugeno fuzzy models. IEEE Trans Fuzzy Syst 124:213–229

    MathSciNet  MATH  Google Scholar 

  35. Kwon OM, Park JH, Lee SM (2010) An improved delay-dependent criterion for asymptotic stability of uncertain dynamic systems with time-varying delays. J Optim Theory Appl 145:343–353

    Article  MathSciNet  MATH  Google Scholar 

  36. Gu K (1994) Integral inequality in the stability problem of Time-Delay systems. In: Proceeding 39th IEEE CDC, Sydney, Philadelphia

  37. Boyd S, Ghoui LE, Feron E, Balakrishnan V (1994) Linear matrix inequalities in system and control theory. SIAM, Philadelphia

    Book  MATH  Google Scholar 

Download references

Acknowledgments

The authors are very much thankful to the editors and anonymous reviewers for their careful reading, constructive comments and fruitful suggestions to improve this manuscript. This work was supported by the National Board for Higher Mathematics, Department of Atomic Energy grant on Ref. No. 2/48(8)/2010/RD II/11191.

Author information

Authors and Affiliations

  1. School of Mathematics, Madurai Kamaraj University, Madurai, 625 021, Tamilnadu, India

    S. Muralisankar, A. Manivannan & N. Gopalakrishnan

Authors
  1. S. Muralisankar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. A. Manivannan
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. N. Gopalakrishnan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to S. Muralisankar.

Additional information

The work of author was supported by NBHM-DAE grant on Ref. No. 2/48(8)/2010/RD II/11191.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Muralisankar, S., Manivannan, A. & Gopalakrishnan, N. Asymptotic stability criteria for T-S fuzzy neural networks with discrete interval and distributed time-varying delays. Neural Comput & Applic 21 (Suppl 1), 357–367 (2012). https://doi.org/10.1007/s00521-012-0936-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-012-0936-z

KeyWords