Skip to main content

Advertisement

Springer Nature Link
Log in

Exponential stability of impulsive stochastic fuzzy cellular neural networks with mixed delays and reaction–diffusion terms

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

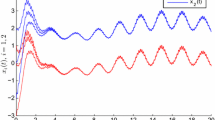
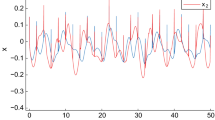
The problem of mean square exponential stability for a class of impulsive stochastic fuzzy cellular neural networks with distributed delays and reaction–diffusion terms is investigated in this paper. By using the properties of M-cone, eigenspace of the spectral radius of nonnegative matrices, Lyapunov functional, Itô’s formula and inequality techniques, several new sufficient conditions guaranteeing the mean square exponential stability of its equilibrium solution are obtained. The derived results are less conservative than the results recently presented in Wang and Xu (Chaos Solitons Fractals 42:2713–2721, 2009), Zhang and Li (Stability analysis of impulsive stochastic fuzzy cellular neural networks with time varying delays and reaction–diffusion terms. World Academy of Science, Engineering and Technology 2010), Huang (Chaos Solitons Fractals 31:658–664, 2007), and Wang (Chaos Solitons Fractals 38:878–885, 2008). In fact, the systems discussed in Wang and Xu (Chaos Solitons Fractals 42:2713–2721, 2009), Zhang and Li (Stability analysis of impulsive stochastic fuzzy cellular neural networks with time varying delays and reaction–diffusion terms. World Academy of Science, Engineering and Technology 2010), Huang (Chaos Solitons Fractals 31:658–664, 2007), and Wang (Chaos Solitons Fractals 38:878–885, 2008) are special cases of ours. Two examples are presented to illustrate the effectiveness and efficiency of the results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Chua LO, Yang L (1988) Cellular neural networks: theory and applications. IEEE Trans Circuits Syst 35(10):1257–1272

    Article  MathSciNet  MATH  Google Scholar 

  2. Roska T, Boros T, Thiran P, Chua LO (1990) Detecting simple motion using Cellular neural networks. In: Proceedings of the IEEE international workshop on cellular neural networks and their applications pp 127–138

  3. Chua LOB, Roska T (1990) Cellular neural networks with nonlinear and delay-type template elements. In: Proceedings of the IEEE international workshop on cellular neural networks and their applications 12-25

  4. Kennedy M, Chua L (1998) Neural networks for nonlinear programming. IEEE Transact Circuits Syst 35:554–562

    Article  MathSciNet  Google Scholar 

  5. Cochocki A, Unbehauen R (1993) Neural networks for optimization and signal processing. John Wily Sons, Stuttgart

    Google Scholar 

  6. Blythe S, Mao X, Liao X (2001) Stability of stochastic delay neural networks. J Franklin Inst 338(5):481–495

    Article  MathSciNet  MATH  Google Scholar 

  7. Cao JD, Zhao HY (2005) New conditions for global exponential stability of cellular neural networks with delays. Neural Netw 18(10):1332–1340

    Article  MATH  Google Scholar 

  8. Chen L, Zhao HY (2008) Stability analysis of stochastic fuzzy cellular neural networks with delays. Neurocomputing 72(1–3):436–444

    Article  Google Scholar 

  9. Kao YG, Gao CC (2008) Global exponential stability analysis for cellular neural networks with variable coeffcients and delays. Neural Comput Appl 17:291–295

    Article  Google Scholar 

  10. Wang X, Xu D (2009) Global exponential stability of impulsive fuzzy cellular neural networks with mixed delays and reaction–diffusion terms. Chaos Solitons Fractals 42:2713–2721

    Article  MathSciNet  MATH  Google Scholar 

  11. Arik S (2002) An improved global stability result for delayed cellular neural networks. IEEE Transact CAS-I 49:1211–1214

    Article  MathSciNet  Google Scholar 

  12. Haykin S (1994) Neural networks. Printice-Hall, NJ

    MATH  Google Scholar 

  13. Huang TW (2006) Exponential stability of fuzzy cellular neural network of distributed delays. Phys Lett A 351(1-2):48–52

    Article  MATH  Google Scholar 

  14. Kao YG, Guo JF, Wang CH, Sun XQ (2012) Delay-dependent robust exponential stability of Markovian jumping reaction–diffusion Cohen-Grossberg neural networks with mixed delays. J Franklin Inst 349(6):1972–1988

    Google Scholar 

  15. Huang TW, Yang T, Li CD (2008) Stability of periodic solution in fuzzy BAM neural networks with finite distributed delays. Neurocomputing 71(16–18):3064–3069

    Article  Google Scholar 

  16. Kao YG, Gao CC, Han W (2010) Global exponential robust stability of reaction–diffusion interval neural networks with continuously distributed delays. Neural Comput Appl 19:867–873

    Article  Google Scholar 

  17. Kwon OM, Park JH (2008) Delay-dependent stability for uncertain cellular neural networks with discrete and distribute time-varying delays. J Franklin Inst 345(7):766–778

    Article  MathSciNet  MATH  Google Scholar 

  18. Lakshmikantham V, Bainov DD, Simeonov PS (1989) Theory of impulsive differential equations. World Scientific, Singapore

    Book  MATH  Google Scholar 

  19. Liao X, Mao X (1996) Exponential stability and instability of stochastic neural networks. Stoch Anal Appl 14(2):165–185

    Article  MathSciNet  MATH  Google Scholar 

  20. Li T, Chong L, Guo L, Sun CY (2009) New results on global asymptotic stability analysis for neural networks with time-varying delays. Nonlinear Anal Real World Appl 10(1):554–562

    Article  MathSciNet  MATH  Google Scholar 

  21. Li ZA, Li KL (2009) Stability analysis of impulsive Cohen-Grossberg neural networks with distributed delays and reaction–diffusion terms. Appl Math Model 33(3):1337–1348

    Article  MathSciNet  MATH  Google Scholar 

  22. Yang S, Shi B, Zhang Q (2012) Complete controllability of nonlinear stochastic impulsive functional systems. Appl Math Comput 218(9):5543–5551

    Article  MathSciNet  MATH  Google Scholar 

  23. Mao X (1997) Stochastic differential equations and applications. Horwood Publishing, Chichester

    MATH  Google Scholar 

  24. Mohammed SEA (1986) Stochastic functional differential equations. Longman, New York

    Google Scholar 

  25. Niculescu SI (2001) Delay effects on stability: a robust approach. Springer, Berlin

    Google Scholar 

  26. Qiu JL (2007) Exponential stability of impulsive neural networks with timevarying delays and reactionC diffusion terms. Neurocomputing 70(4–6):1102–1108

    Article  Google Scholar 

  27. Song Qk, Cao JD (2008) Dynamical behaviors of discrete-time fuzzy cellular neural networks with variable delays and impulsives. J Franklin Inst 345(1):39–59

    Article  MathSciNet  MATH  Google Scholar 

  28. Song QK, Wang ZD (2008) Stability analysis of impulsive stochastic Cohen-Grossberg neural networks with mixed time delays. Phys A 387(13):3314–3326

    Article  Google Scholar 

  29. Sun Y, Cao JD (2007) Pth moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Anal Real World Appl 8(5):1171–1185

    Article  MathSciNet  MATH  Google Scholar 

  30. Sun WW, Chen YM (2009) Global asymptotic stability analysis for neutral stochastic neural networks with time-varying delays. Commun Nonlinear Sci Numer Simul 14(4):1576–1581

    Article  MathSciNet  Google Scholar 

  31. Wang Z, Fang J, Liu X (2008) Global stability of stochastic high-order neural networks with discrete and distributed delays. Chaos Solitons Fractals 36(2):388–396

    Article  MathSciNet  MATH  Google Scholar 

  32. Wang XH, Guo QY, Xu DY (2009) Exponential p-stability of impulsive stochastic Cohen-Grossberg neural networks with mixed delays. Math Comput Simul 79(5):1698–1710

    Article  MathSciNet  MATH  Google Scholar 

  33. Wang Q, Liu X (2007) Exponential stability of impulsive cellular neural networks with time delay via Lyapunov functionals. Appl Math Comput 194(1):186–198

    Article  MathSciNet  MATH  Google Scholar 

  34. Wan L, Sun J (2005) Convergence dynamics of stochastic reaction–diffusion recurrent neural networks with delays. Int J Bifurcat Chaos 15(7):2133–2144

    MathSciNet  Google Scholar 

  35. Xu LG, Xu DY (2009) Exponential p-stability of impulsive stochastic neural networks with mixed delays. Chaos Solitons Fractals 41(1):263–272

    Article  MathSciNet  MATH  Google Scholar 

  36. Yang T (2001) Impulsive systems and control: theory and application. Nova Science Publishers, New york

    Google Scholar 

  37. Yang T, Yang LB, Wu CW, Chua LO (1996) Fuzzy cellular neural network: Theory. In: Proceedings of IEEE international workshop on cellular neural networks and applications (CNNA'96) 225–230

  38. Yang T, Yang LB (1996) The global stability of fuzzy cellular neural networks. IEEE Transact Circuits Syst I 43:880–883

    Article  Google Scholar 

  39. Yuan K, Cao JD, Deng JM (2006) Exponential stability and periodic solutions of fuzzy cellular neural networks with time-varying delays. Neurocomputing 69(13-15):1619–1627

    Article  Google Scholar 

  40. Zhang QH, Xiang RG (2008) Global asymptotic stability of fuzzy cellular neural networks with time-varying delays. Phys Lett A 372(22):3971–3977

    Article  MathSciNet  MATH  Google Scholar 

  41. Zhao HY, Ding N, Chen L (2007) Almost sure exponential stability of stochastic fuzzy cellular neural networks with delays. Chaos Solitons Fractals 40(4):1653–1659

    Article  MathSciNet  Google Scholar 

  42. Xu DY, Yang ZG, Yang ZC (2007) Exponential stability of nonlinear impulsive neutral differential equations with delays. Nonlinear Anal 67:1426–1439

    Article  MathSciNet  MATH  Google Scholar 

  43. Xu DY, Yang ZC (2005) Impulsive delay differential inequality and stability of neural networks. J Math Anal Appl 305:107–120

    Article  MathSciNet  MATH  Google Scholar 

  44. Xu DY, Zhu W, Long SJ (2006) Global exponential stability of impulsive integro-differential equation. Nonlinear Anal 64:2805–2816

    Article  MathSciNet  MATH  Google Scholar 

  45. Song Q, Cao J (2005) Global exponential stability and existence of periodic solutions in BAM networks with delays and reaction–diffusion terms. Chaos Solitons Fractals 23:421–430

    Article  MathSciNet  MATH  Google Scholar 

  46. Song Q, Zhao Z, Li Y (2005) Global exponential stability of BAM neural networks with distributed delays and reaction–diffusion terms. Phys Lett A 335:213–225

    Article  MATH  Google Scholar 

  47. Wang C, Kao Y, Yang G (2012) Exponential stability of impulsive stochastic Fuzzy reaction–diffusion Cohen-Grossberg neural networks with mixed delays. Neurocomputing 89:55–63

    Article  Google Scholar 

  48. Hasting A (1978) Global stability in Lotka-Volterra systems with diffusion. J Math Biol 6:163–168

    Article  MathSciNet  Google Scholar 

  49. Liao X, Li C (1997) Stability in Gilpin-Ayala competition models with diffusion. Nonlinear Anal TMA 18:1751–1758

    Article  MathSciNet  Google Scholar 

  50. Rothe F (1976) Convergence to the equilibrium state in the Volterra-Lotka diffusion equations. J Math Biol 3:319–324

    Article  MathSciNet  MATH  Google Scholar 

  51. Liang J, Cao J (2003) Global exponential stability of reaction–diffusion recurrent neural networks with time-varying delays. Phys Lett A 314:434–442

    Article  MathSciNet  MATH  Google Scholar 

  52. Berman A, Plemmons RJ (1979) Nonnegative matrices in mathematical sciences. Academic, New York

    MATH  Google Scholar 

  53. Horn RA, Johnson CR (1985) Matrix analysis. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  54. Wang X, Guo Q, Xu D (2009) Exponential p-stability of impulsive stochastic Cohen-Grossberg neural networks with mixed delays. Math Comput Simul 79:1698–1710

    Article  MathSciNet  MATH  Google Scholar 

  55. Lu JG (2008) Global exponential stability and periodicity of reaction–diffusion delayed recurrent neural networks with Dirichlet boundary conditions. Chaos Solitons Fractals 35:116–125

    Article  MathSciNet  MATH  Google Scholar 

  56. Zhang X, Li K (2010) Stability analysis of impulsive stochastic fuzzy cellular neural networks with time varying delays and reaction–diffusion terms. World Academy of Science, Engineering and Technology 61

  57. Huang TW (2007) Exponential stability of delayed fuzzy cellular neural networks with diffusion. Chaos Solitons Fractals 31:658–664

    Article  MathSciNet  MATH  Google Scholar 

  58. Wang J, Lu JG (2008) Global exponential stability of fuzzy cellular neural networks with delays and reaction–diffusion terms. Chaos Solitons Fractals 38:878–885

    Article  MathSciNet  MATH  Google Scholar 

  59. Chen L, Wu R, Pan D (2011) Mean square exponential stability of impulsive stochastic fuzzy cellular neural networks with distributed delays. Expert Syst Appl 38:6294–6299

    Article  Google Scholar 

  60. Tank DW, Hopfield JJ (1987) Neural computation by concentrating information in time. Proc Natl Acad Sci USA 84(7):1896–900

    Article  MathSciNet  Google Scholar 

  61. Kao Y, Gao C (2007) Global Exponential Stability for Almost Periodic Solution of Competitive Neural Networks with Distributed Delays. Math Pract Theory 37(23):120–125

    MathSciNet  MATH  Google Scholar 

  62. Zhao Y, Zhang L, Shen S, Gao H (2011) Robust stability criterion for discrete-time uncertain Markovian jumping neural networks with defective statistics of modes transitions. IEEE Trans Neural Netw 22(1):164–170

    Article  Google Scholar 

  63. Zhang L, Cui N, Liu M, Zhao Y (2011) Asynchronous filtering of discrete-time switched linear systems with average dwell time. IEEE Transact Circuits Syst-I 58(5):1109–1118

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors would like to thank the editors and the anonymous reviewers for their valuable comments and constructive suggestions. This research is supported by the Natural Science Foundation of Guangxi Autonomous Region (No. 2012GXNSFBA053003), the National Natural Science Foundations of China (60973048, 60974025, 60673101, 60939003), National 863 Plan Project (2008 AA04Z401, 2009AA043404), the Natural Science Foundation of Shandong Province (No. Y2007G30), the Scientific and Technological Project of Shandong Province (No. 2007GG3WZ04016), the Science Foundation of Harbin Institute of Technology (Weihai) (HIT(WH)200807), the Natural Scientific Research Innovation Foundation in Harbin Institute of Technology (HIT.NSRIF. 2001120), the China Postdoctoral Science Foundation (2010048 1000) and the Shandong Provincial Key Laboratory of Industrial Control Technique (Qingdao University).

Author information

Authors and Affiliations

  1. Department of Mathematics, Harbin Institute of Technology, Weihai, 264209, China

    Guowei Yang, Yonggui Kao, Wei Li & Sun Xiqian

  2. College of Information Engineering, Nanchang Hangkong University, Nanchang, 330063, China

    Guowei Yang

Authors
  1. Guowei Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yonggui Kao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Wei Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Sun Xiqian
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yonggui Kao.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yang, G., Kao, Y., Li, W. et al. Exponential stability of impulsive stochastic fuzzy cellular neural networks with mixed delays and reaction–diffusion terms. Neural Comput & Applic 23, 1109–1121 (2013). https://doi.org/10.1007/s00521-012-1040-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-012-1040-0

Keywords