Skip to main content
Springer Nature Link
Log in

A new pruning method for decision tree based on structural risk of leaf node

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

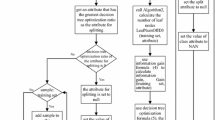
Pruning is an effective technique in improving the generalization performance of decision tree. However, most of the existing methods are time-consuming or unsuitable for small dataset. In this paper, a new pruning algorithm based on structural risk of leaf node is proposed. The structural risk is measured by the product of the accuracy and the volume (PAV) in leaf node. The comparison experiments with Cost-Complexity Pruning using cross-validation (CCP-CV) algorithm on some benchmark datasets show that PAV pruning largely reduces the time cost of CCP-CV, while the test accuracy of PAV pruning is close to that of CCP-CV.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Breiman L, Friedman J, Olshen R, Stone C (1984) Classification and regression trees. Wadsworth International, Belmont

    MATH  Google Scholar 

  2. Zhong M, Georgiopoulos M, Anagnostopoulos G (2008) A k-norm pruning algorithm for decision tree classifiers based on error rate estimation. Mach Learn 71(1):55–88

    Article  Google Scholar 

  3. Chandra B, Kothari R, Paul P (2010) A new node splitting measure for decision tree construction. Pattern Recogn 43(8):2725–2731

    Article  MATH  Google Scholar 

  4. Breiman L (1996) Technical note: some properties of splitting criteria. Mach Learn 24(1):41–47

    MathSciNet  MATH  Google Scholar 

  5. Bohanec M, Bratko I (1994) Trading accuracy for simplicity in decision trees. Mach Learn 15(3):223–250

    MATH  Google Scholar 

  6. Esposito F, Malerba D, Semeraro G (1997) A comparative analysis of methods for pruning decision trees. IEEE Trans Pattern Anal Mach Intell 19(5):476–491

    Article  Google Scholar 

  7. Leonard A, Wavid W (1997) Simplifying decision trees: a survey. Knowl Eng Rev 12(1):1–40

    Article  Google Scholar 

  8. Mingers J (1989) An empirical comparison of pruning methods for decision tree induction. Mach Learn 4(2):227–243

    Article  Google Scholar 

  9. Windeatt T, Ardeshir G (2001) An empirical comparison of pruning methods for ensemble classifiers. In: Proceedings of the 4th international conference on advances in intelligent data analysis, pp 208–217

  10. Niblett T, Bratko I (1986) Learning decision rules in noisy domains. In: Proceedings of expert systems’86. Cambridge University Press, New York, pp 25–34

  11. Quinlan J (1987) Simplifying decision trees. Int J Man Mach Stud 27(3):221–234

    Article  Google Scholar 

  12. Kim J, Kim Y (2006) Maximum a posteriori pruning on decision trees and its application to bootstrap BUMPing. Comput Stat Data Anal 50(3):710–719

    Article  MATH  Google Scholar 

  13. Richard O, Peter E, David G (2000) Pattern classification, 2nd edn. Wiley, New York

    Google Scholar 

  14. Buntine W, Niblett T (1992) A further comparison of splitting rules for decision-tree Induction. Mach Learn 8(1):75–85

    Google Scholar 

  15. Blake C, Merz C (1998) UCI repository of machine learning databases. Dept. of Information and Computer Sciences, University of California, Irvine. http://www.ics.uci.edu/~mlearn/MLRepository.html

Download references

Acknowledgments

This work was partially supported by the Natural Science Foundations of Fujian Province of China under Grant No.2011J01373 and the Foundation of Key Laboratory of System Control and Information Processing, Ministry of Education, P.R. China under Grant No. SCIP2011004.

Conflict of interest

None declared.

Author information

Authors and Affiliations

  1. Department of Automation, Xiamen University, Xiamen, 361005, People’s Republic of China

    Linkai Luo, Xiaodong Zhang, Hong Peng, Weihang Lv & Yan Zhang

Authors
  1. Linkai Luo
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiaodong Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Hong Peng
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Weihang Lv
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Yan Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Linkai Luo.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Luo, L., Zhang, X., Peng, H. et al. A new pruning method for decision tree based on structural risk of leaf node. Neural Comput & Applic 22 (Suppl 1), 17–26 (2013). https://doi.org/10.1007/s00521-012-1055-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-012-1055-6

Keywords