Skip to main content
Springer Nature Link
Log in

Optimal control problem via neural networks

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

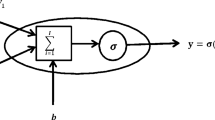
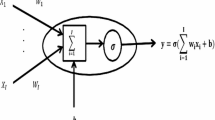
This paper attempts to propose a new method based on capabilities of artificial neural networks, in function approximation, to attain the solution of optimal control problems. To do so, we try to approximate the solution of Hamiltonian conditions based on the Pontryagin minimum principle (PMP). For this purpose, we introduce an error function that contains all PMP conditions. In the proposed error function, we used trial solutions for the trajectory function, control function and the Lagrange multipliers. These trial solutions are constructed by using neurons. Then, we minimize the error function that contains just the weights of the trial solutions. Substituting the optimal values of the weights in the trial solutions, we obtain the optimal trajectory function, optimal control function and the optimal Lagrange multipliers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Krabs W, Pickl S (2010) An optimal control problem in cancer chemotherapy. Appl Math Comput 217:1117–1124

    Article  MathSciNet  MATH  Google Scholar 

  2. Modares H, Naghibi Sistani MB (2011) Solving nonlinear optimal control problems using a hybrid IPSOSQP algorithm. Eng Appl Artif Intell 24:476–484

    Article  Google Scholar 

  3. Kirk DE (2004) Optimal control theory—an introduction. Dover Publications, Mineola, NY

    Google Scholar 

  4. Lewis F, Syrmos VL (1995) Optimal control. Wiley, New York

    Google Scholar 

  5. Hilscher RS, Zeidan V (2012) Hamilton–Jacobi theory over time scales and applications to linear-quadratic problems. Nonlinear Anal 75:932–950

    Article  MathSciNet  MATH  Google Scholar 

  6. Berkani S, Manseur F, Maidi A (2012) Optimal control based on the variational iteration method. Comput Math Appl 64:604–610

    Article  MathSciNet  MATH  Google Scholar 

  7. Garg D, Patterson M, Hagera WW, Raoa AV, Bensonb DA, Huntington GT (2010) A unified framework for the numerical solution of optimal control problems using pseudo-spectral methods. Automatica 46:1843–1851

    Article  MATH  Google Scholar 

  8. Clever D, Lang J, Ulbrich S, Ziems JC (2010) Combination of an adaptive multilevel SQP method and a space-time adaptive PDAE solver for optimal control problems. Procedia Comput Sci 1:1435–1443

    Article  Google Scholar 

  9. de Oliveira VA, Silva GN, Rojas-Medar MA (2009) KT-invexity in optimal control problems. Nonlinear Anal 71:4790–4797

    Article  MathSciNet  MATH  Google Scholar 

  10. Gerdts M (2008) A non-smooth Newtons method for control-state constrained optimal control problems. Math Comput Simul 79:925–936

    Article  MathSciNet  MATH  Google Scholar 

  11. Buldaev AS (2008) Perturbation methods in optimal control problems. Ecol Model 216:157–159

    Article  Google Scholar 

  12. Salama AA (2006) Numerical methods based on extended one-step methods for solving optimal control problems. Appl Math Comput 183:243–250

    Article  MathSciNet  MATH  Google Scholar 

  13. Zhou YY, Yangb XQ, Teob KL (2006) The existence results for optimal control problems governed by a variational inequality. J Math Anal Appl 321:595–608

    Article  MathSciNet  MATH  Google Scholar 

  14. Chryssoverghi I, Coletsos I, Kokkinis B (2006) Discretization methods for optimal control problems with state constraints. J Comput Appl Math 191:1–31

    Article  MathSciNet  MATH  Google Scholar 

  15. England R, Gomez S, Lamourc R (2005) Expressing optimal control problems as differential algebraic equations. Comput Chem Eng 29:1720–1730

    Article  Google Scholar 

  16. Rodriguez A (2004) On the local stability of the solution to optimal control problems. J Econ Dyn Control 28:2475–2484

    Article  MATH  Google Scholar 

  17. Saberi Nik H, Effati S, Shirazian M (2012) An approximate-analytical solution for the Hamilton–Jacobi–Bellman equation via homotopy perturbation method. Appl Math Model 36(11):5614–5623

    Google Scholar 

  18. Cheng T, Sun H, Qu Z, Lewis FL (2009) Neural network solution for suboptimal control of non-holonomic chained form system. Trans Inst Measurement Control 31(6):475–494

    Article  Google Scholar 

  19. Cheng T, Lewis FL (2007) Neural network solution for finite-horizon H-infinity constrained optimal control of nonlinear systems. J Control Theory Appl 5(1):1–11

    Article  MathSciNet  Google Scholar 

  20. Cheng T, Lewis FL, Abu-Khalaf M (2007) Fixed-final-time-constrained optimal control of nonlinear systems using neural network HJB approach. IEEE Trans Neural Netw 18(6):1725–1737

    Google Scholar 

  21. Vrabie D, Lewis FL (2009) Neural network approach to continuous-time direct adaptive optimal control for partially unknown nonlinear systems. Neural Netw 22:237–246

    Article  Google Scholar 

  22. Lagaris IE, Likas A (2012) Hamilton–Jacobi theory over time scales and applications to linear-quadratic problems. IEEE Trans Neural Netw 9(5):987–1000

    Article  Google Scholar 

  23. Keckman V (2001) Learning and soft computing. MIT press, Cambridge, MA

    Google Scholar 

  24. Rubio JE (1986) Control and optimization, the linear treatment of nonlinear problems. Manchester University Press, Manchester

    MATH  Google Scholar 

  25. Shirazian M, Effati S (2012) Solving a class of nonlinear optimal control problems via he’s variational iteration method. Int J Control Automat Syst 10(2):249–256

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Ferdowsi University of Mashhad, Mashhad, Iran

    Sohrab Effati & Morteza Pakdaman

  2. Center of Excellence on Soft Computing and Intelligent Information Processing, Ferdowsi University of Mashhad, Mashhad, Iran

    Sohrab Effati & Morteza Pakdaman

Authors
  1. Sohrab Effati
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Morteza Pakdaman
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Morteza Pakdaman.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Effati, S., Pakdaman, M. Optimal control problem via neural networks. Neural Comput & Applic 23, 2093–2100 (2013). https://doi.org/10.1007/s00521-012-1156-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-012-1156-2

Keywords