Skip to main content

Advertisement

Springer Nature Link
Log in

Global exponential stability of a class of memristive neural networks with time-varying delays

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

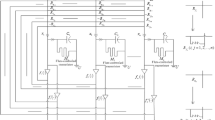
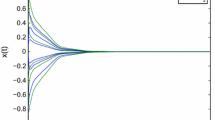
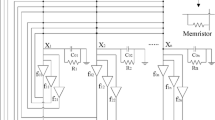
This paper studies the uniqueness and global exponential stability of the equilibrium point for memristor-based recurrent neural networks with time-varying delays. By employing Lyapunov functional and theory of differential equations with discontinuous right-hand side, we establish several sufficient conditions for exponential stability of the equilibrium point. In comparison with the existing results, the proposed stability conditions are milder and more general, and can be applied to the memristor-based neural networks model whose connection weight changes continuously. Numerical examples are also presented to show the effectiveness of the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Chua LO (1971) Memristor—the missing circuit element. IEEE Trans Circuit Theory 18(5):507–519

    Article  Google Scholar 

  2. Strukov DB, Snider GS, Stewart DR, Williams RS (2008) The missing memristor found. Nature 453:80–83

    Article  Google Scholar 

  3. Pershin YV, Ventra MD (2008) Spin memristive systems: spinmemory effects in semiconductor spintronics. Phys Rev B 78(11):1–4

    Article  Google Scholar 

  4. Yang JJ, Pickett MD, Li X, Ohlberg DAA, Stewart DR, Williams RS (2008) Memristive switching mechanism formetal/oxide/metal nanodevices. Nat Nanotechnol 3(7):429–433

    Article  Google Scholar 

  5. Wang X, Chen Y, Xi H, Li H, Dimitrov D (2009) Spintronic memristor through spin-torque-induced magnetization motion. IEEE Electron Device Lett 30(3):294–297

    Article  Google Scholar 

  6. Itoh M, Chua LO (2008) Memristor oscillators. Int J Bifurcat Chaos 18:3183–3206

    Article  MathSciNet  MATH  Google Scholar 

  7. Itoh M, Chua LO (2009) Memristor cellular automata and memristor discrete-time cellular neural networks. Int J Bifurcat Chaos 19:3605–3656

    Article  MathSciNet  MATH  Google Scholar 

  8. Hu J, Wang J (2010) Global uniform asymptotic stability of memristor-based recurrent neural networks with time delay. In: 2010 international joint conference on neural networks (IJCNN2010), pp 1–8, Barcelona, Spain

  9. Wu AL, Gang Z, Zhu X, Zhang J (2011) Exponential synchronization of memristor-based recurrent neural networks with time delays. Neurocomputing 74:3043–3050

    Article  Google Scholar 

  10. Zhang GD, Shen Y, Sun JW (2012) Global exponential stability of a class of memristor-based recurrent neural networks with time-varying delays. Neurocomputing 35(1):47–59

    Google Scholar 

  11. Wu AL, Zhang J, Zeng ZG (2011) Dynamic behaviors of a class of memristor-based Hopfield networks. Phys Lett A 375:1661–1665

    Article  MathSciNet  MATH  Google Scholar 

  12. Liao XF, Wong KW (2004) Global exponential stability for a class of retarded functional differential equations with applications in neural networks. J Math Appl 293:125–148

    MathSciNet  MATH  Google Scholar 

  13. Liao XF, Wong KW, Wu ZF (2001) Bifurcation analysis on a two-neuron system with distributed delays. Phys D 140:123–141

    Article  MathSciNet  Google Scholar 

  14. Liao XF, Wong KW, Leung CS, Wu ZF (2002) Hopf bifurcation and chaos in a single delayed neuron equation with non-monotonic activation function. Chaos, Solitons Fractals 12:1535–1547

    Article  MathSciNet  Google Scholar 

  15. Li CJ, Li CD, Huang T (2011) Exponential stability of impulsive high-order Hopfield-type neural networks with delays and reaction-diffusion. Int J Comput Math 88(15):3150–3162

    Article  MathSciNet  MATH  Google Scholar 

  16. Li CJ, Li CD, Huang TW, Liao XF (2011) Impulsive effects on stability of high-order BAM neural networks with time delays. Neurocomputing 74:1541–1550

    Article  Google Scholar 

  17. Lu DJ, Li CJ. Exponential stability of stochastic high-order BAM neural networks with time delays and impulsive effects. Neural Comput Appl. doi:10.1007/s00521-012-0861-1

  18. Li CD, Li CJ, Liu C (2009) Destabilizing effects of impulse in delayed BAM neural networks. Mod Phys Lett B 23(29):3503–3513

    Article  MATH  Google Scholar 

  19. Liao XF, Yu JB (1998) Robust stability for interval Hopfield neural networks with time delays. IEEE Trans Neural Netw 9:1042–1046

    Article  Google Scholar 

  20. Li CD, Liao XF (2006) Delay-dependent and delay-independent stability criteria for cellular neural networks with delay. Int J Bifurcat Chaos 16(11):3323–3340

    Article  MathSciNet  MATH  Google Scholar 

  21. He X, Li CD, Shu Y (2012) Bogdanov–Takens bifurcation in a single inertial neuron model with delay. Neurocomputing 89(15):193–201

    Article  Google Scholar 

  22. Zhang L, Yi Z (2011) Selectable and unselectable sets of neurons in recurrent neural networks with saturated piecewise linear transfer function. IEEE Trans Neural Networks 22:1021–1031

    Article  Google Scholar 

  23. Filippov AF (1988) Differential equations with discontinuous right-hand sides. Kluwer, Dordrecht

    Book  MATH  Google Scholar 

  24. Wen S, Zeng Z, Huang T (2012) Adaptive synchronization of memristor-based Chua’s circuits. Phys Lett A 376:2775–2780

    Article  Google Scholar 

  25. Wen S, Zeng Z, Huang T (2012) Exponential stability analysis of memristor-based recurrent neural networks with time-varying delays. Neurocomputing 97:233–240

    Article  Google Scholar 

  26. Wen S, Zeng Z (2012) Dynamics analysis of a class of memristor-based recurrent networks with time-varying delays in the presence of strong external stimuli. Neural Process Lett 35(1):47–59

    Article  Google Scholar 

Download references

Acknowledgments

This works is supported by the Graduate Innovation Foundation of Chongqing University Grant No. CDJXS12 18 00 05 and NPRP 4-1162- 1-181 funded by Qatar National Research Fund, Qatar.

Author information

Authors and Affiliations

  1. College of Computer Science, Chongqing University, Chongqing, 400044, China

    Xin Wang & Chuandong Li

  2. Texas A&M University at Qatar, Doha, 23874, Qatar

    Tingwen Huang

  3. School of Electronic and Information Engineering, Southwest University, Chongqing, 400715, China

    Shukai Duan

Authors
  1. Xin Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Chuandong Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Tingwen Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Shukai Duan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Chuandong Li.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, X., Li, C., Huang, T. et al. Global exponential stability of a class of memristive neural networks with time-varying delays. Neural Comput & Applic 24, 1707–1715 (2014). https://doi.org/10.1007/s00521-013-1383-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-013-1383-1

Keywords