Abstract
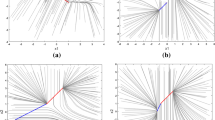
A winner-take-all Lotka–Volterra recurrent neural network with N × N neurons is proposed in this paper. Sufficient conditions for existence of winner-take-all stable equilibrium points in the network are obtained. These conditions guarantee that there is one and only one winner in each row and each column at any stable equilibrium point. In addition, rigorous convergence analysis is carried out. It is proven that the proposed network model is convergent. The conditions for the winner-take-all behavior obtained in this paper provide design guidelines for network implementation and fabrication. Simulations are also presented to illustrate the theoretical findings.


Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Urahama K, Nagao T (1995) k-Winner-take-all circuit with O(N) complexity. IEEE Trans Neural Netw 6:775–778
Wang L (1999) Multi-associative neural networks and their applications to learning and retrieving complex spatio-temporal sequences. IEEE Trans Syst Man Cybern Part B Cybern 29:73–82
Wang L (1997) On competitive learning. IEEE Trans Neural Netw 8:1214–1217
Dempsey GL, McVey ES (1993) Circuit implementation of a peak detector neural network. IEEE Trans Circuits Syst II Analog Digital Signal Process 40:585–591
Seiler G, Nossek JA (1993) Winner-take-all cellular neural networks. IEEE Trans Circuits Syst II Analog Digit Signal Process 40:184–190
Andrew LLH (1996) Improving the robustness of winner-take-all cellular neural networks. IEEE Trans Circuits Syst II Analog Digit Signal Process 43:329–334
Fukai T, Tanaka S (1997) A simple neural network exhibiting selective activation of neuronal ensembles: from winner-take-all to winner-share-all. Neural Comput 9:77–97
Asai T, Fukai T, Tanaka S (1999) A subthreshold MOS circuit for the Lotka–Volterra neural network producing the winner-take-all solutions. Neural Netw 12:211–216
Hahnloser RHR (1998) On the piecewise analysis of networks of linear threshold neurons. Neural Netw 11:691–697
Tang HJ, Tan KC, Zhang W (2005) Analysis of cyclic dynamics for networks of linear threshold neurons. Neural Comput 17:97–114
Qu H, Yi Z, Wang X (2009) A winner-take-all neural networks of N linear threshold neurons without self-excitatory connections. Neural Process Lett 29:143–154
Yi Z, Heng PA, Fung PF (2000) Winner-take-all discrete recurrent neural networks. IEEE Trans Circuits Syst II Analog Digit Signal Process 47:1584–1589
Wang J (2010) Analysis and design of a k-winners-take-all model with a single state variable and the heaviside step activation function. IEEE Trans Neural Netw 21:1496–1506
Liu Q, Dang C, Cao J (2010) A novel recurrent neural network with one neuron and finite-time convergence for k-winners-take-all operation. IEEE Trans Neural Netw 21:1140–1148
Yang JF, Chen CM (1997) A dynamic k-winners-take-all neural network. IEEE Trans Syst Man Cybern Part B Cybern 27:523–526
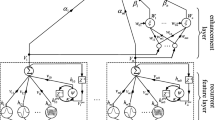
Wersing H, Steil JJ, Ritter H (2001) A competitive layer model for feature binding and sensory segmentation. Neural Comput 13:357–387
Yi Z (2010) Foundations of implementing the competitive layer model by Lotka–Volterra recurrent neural networks. IEEE Trans Neural Netw 21:494–507
Zheng B, Yi Z (2012) A new method based on the CLM of the LV RNN for brain MR image segmentation. Digit Signal Process 22:497–505
Yi Z, Tan KK (2004) Convergence analysis of recurrent neural networks. Kluwer, Dordrecht
Acknowledgments
The authors wish to thank the reviewers for their valuable comments and helpful suggestions. A project supported by Scientific Research Fund of SiChuan Provincial Education Department (12ZA172). This work was also partly supported by the Foundation of the China West Normal University under Grant 10A003 and 12B023.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zheng, B. A winner-take-all Lotka–Volterra recurrent neural network with only one winner in each row and each column. Neural Comput & Applic 24, 1749–1757 (2014). https://doi.org/10.1007/s00521-013-1412-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-013-1412-0