Skip to main content

Advertisement

Springer Nature Link
Log in

Weights and structure determination of multiple-input feed-forward neural network activated by Chebyshev polynomials of Class 2 via cross-validation

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

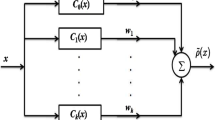
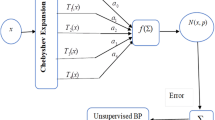
Differing from conventional improvements on backpropagation (BP) neural network, a novel neural network is proposed and investigated in this paper to overcome the BP neural-network weaknesses, which is called the multiple-input feed-forward neural network activated by Chebyshev polynomials of Class 2 (MINN-CP2). In addition, to obtain the optimal number of hidden-layer neurons and the optimal linking weights of the MINN-CP2, the paper develops an algorithm of weights and structure determination (WASD) via cross-validation. Numerical studies show the effectiveness and superior abilities (in terms of approximation and generalization) of the MINN-CP2 equipped with the algorithm of WASD via cross-validation. Moreover, an application to gray image denoising demonstrates the effective implementation and application prospect of the proposed MINN-CP2 equipped with the algorithm of WASD via cross-validation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Yu S, Zhu K, Diao F (2008) A dynamic all parameters adaptive BP neural networks model and its application on oil reservoir prediction. Appl Math Comput 195:66–75

    Article  MATH  MathSciNet  Google Scholar 

  2. Liang L, Wu D (2005) An application of pattern recognition on scoring Chinese corporations financial conditions based on backpropagation neural network. Comput Oper Res 32:1115–1129

    Article  Google Scholar 

  3. Zhang Y, Jiang D, Wang J (2002) A recurrent neural network for solving Sylvester equation with time-varying coefficients. IEEE Trans Neural Netw 13:1053–1063

    Article  Google Scholar 

  4. Izeboudjen N, Bouridane A, Farah A, Bessalah H (2012) Application of design reuse to artificial neural networks: case study of the back propagation algorithm. Neural Comput Appl 21:1531–1544

    Article  Google Scholar 

  5. Dehuri S, Cho SB (2010) A comprehensive survey on functional link neural networks and an adaptive PSO-BP learning for CFLNN. Neural Comput Appl 19:187–205

    Article  Google Scholar 

  6. Wang W, Yu B (2009) Text categorization based on combination of modified back propagation neural network and latent semantic analysis. Neural Comput Appl 18:875–881

    Article  Google Scholar 

  7. Zhang Y, Li W, Yi C, Chen K (2008) A weights-directly-determined simple neural network for nonlinear system identification. In: Proceedings of the IEEE international conference on fuzzy systems, pp 455–460

  8. Zhang Y, Li L, Yang Y, Ruan G (2009) Euler neural network with its weight-direct-determination and structure-automatic-determination algorithms. In: Proceedings of the 9th international conference on hybrid intelligent systems, pp 319–324

  9. Zhang Y, Chen J, Guo D, Yin Y, Lao W (2012) Growing-type weights and structure determination of 2-input Legendre orthogonal polynomial neuronet. In: Proceedings of the IEEE international symposium on industrial electronics, pp 852–857

  10. Qin T, Chen Z, Zhang H, Li S, Xiang W, Li M (2004) A learning algorithm of CMAC based on RLS. Neural Process Lett 19:49–61

    Article  Google Scholar 

  11. Qin T, Zhang H, Chen Z, Xiang W (2005) Continuous CMAC-QRLS and its systolic array. Neural Process Lett 22:1–16

    Article  Google Scholar 

  12. Chen S, Cowan C, Grant P (1991) Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans Neural Netw 2:302–309

    Article  Google Scholar 

  13. Chen S, Billings S, Luo W (1989) Orthogonal least squares methods and their application to non-linear system identification. Int J Control 50:1873–1896

    Article  MATH  MathSciNet  Google Scholar 

  14. Chen S, Wu Y, Luk B (1999) Combined genetic algorithm optimization and regularized orthogonal least squares learning for radial basis function networks. IEEE Trans Neural Netw 10:1239–1243

    Article  Google Scholar 

  15. Montana D, Davis L (1989) Training feedforward neural networks using genetic algorithms. In: Proceedings of the international joint conferences on artificial intelligence, pp 762–767

  16. Huang G, Zhu Q, Siew C (2006) Extreme learning machine: a new learning scheme of feedforward neural networks. Neurocomputing 70:489–501

    Article  Google Scholar 

  17. Bebis G, Georgiopoulos M (1994) Feed-forward neural networks. IEEE Potentials 13:27–31

    Article  Google Scholar 

  18. Boyd JP (2000) Chebyshev and Fourier spectral methods, 2nd edn. Dover Publications, New York

    Google Scholar 

  19. Liang X, Li Q (2005) Multivariable approximation. National Defense Industry Press, Beijing

    Google Scholar 

  20. Ibrahim B, Ertan I (2008) Direct and converse results for multivariate generalized Bernstein polynomials. J Comput Appl Math 219:145–155

    Article  MATH  MathSciNet  Google Scholar 

  21. Dunkl C, Xu Y (2001) Orthognal polynomials of several variables. Cambridge University Press, Cambridge

    Book  Google Scholar 

  22. Zhang Y, Li K, Tan N (2009) An RBF neural network classifier with centers, variances and weights directly determined. Comput Technol Autom 28:5–9

    Google Scholar 

  23. Zhang Y, Tan N (2010) Weights direct determination of feedforward neural networks without iterative BP-training (chapter 10). In: Wang LS, Hong T (eds) Intelligent soft computation and evolving data mining: integrating advanced technologies. IGI Global, Hershey

    Google Scholar 

  24. Zhang Y, Yu X, Xiao L, Li W, Fan Z (2013) Weights and structure determination of artificial neuronets (chapter 5). In: Zhang WJ (ed) Self-organization: theories and methods. Nova Science, New York

    Google Scholar 

  25. Zhang Y, Li W (2009) Gegenbauer orthogonal basis neural network and its weights-direct-determination method. Electron Lett 45:1184–1185

    Article  Google Scholar 

  26. Zhang G, Hu M, Patuwo B, Indro D (1999) Artificial neural networks in bankruptcy prediction general framework and cross-validation analysis. Eur J Oper Res 116:16–32

    Article  MATH  Google Scholar 

  27. Mi X, Zou Y, Wei W, Ma K (2005) Testing the generalization of artificial neural networks with cross-validation and independent-validation in modelling rice tillering dynamics. Ecol Model 181:493–508

    Article  Google Scholar 

  28. Engel J (1996) Choosing an appropriate sample interval for instantaneous sampling. Behav Process 38:11–17

    Article  Google Scholar 

  29. Pawlus P, Zelasko W (2012) The importance of sampling interval for rough contact mechanics. Wear 276–277:121–129

    Article  Google Scholar 

  30. Ji Z, Chen Q, Sun Q, Xia D (2009) A moment-based nonlocal-means algorithm for image denoising. Inf Process Lett 109:1238–1244

    Article  MATH  MathSciNet  Google Scholar 

  31. Nguyen-Thien T, Tran-Cong T (1999) Approximation of functions and their derivatives a neural network implementation with applications. Appl Math Model 23:687–704

    Article  MATH  Google Scholar 

  32. Huang G, Saratchandran P, Sundararajan N (2005) A generalized growing and pruning RBF (GGAP-RBF) neural network for function approximation. IEEE Trans Neural Netw 16(1):57–67

    Article  Google Scholar 

  33. Gonzalez R, Woods R (2003) Digital image processing, 2nd edn. Publishing House of Electronics Industry, Beijing

    Google Scholar 

  34. http://www.imageprocessingplace.com/

  35. Ibnkahla M (2007) Neural network modeling and identification of nonlinear MIMO channels. In: Proceedings of the 9th international symposium on signal processing and its applications, pp 1–4

  36. Zhang T, Zhou C, Zhu Q (2009) Adaptive variable structure control of MIMO nonlinear systems with time-varying delays and unknown dead-zones. Int J Autom Comput 6:124–136

    Article  Google Scholar 

Download references

Acknowledgments

The authors would like to thank the editors and anonymous reviewers sincerely for their time and effort spent in handling the paper, as well as many constructive comments provided for improving much further the presentation and quality of the paper. This work is supported by the Specialized Research Fund for the Doctoral Program of Institutions of Higher Education of China (with Project Number 20100171110045), the National Innovation Training Program for University Students (with Project Number 201210558042), and the 2012 Scholarship Award for Excellent Doctoral Student Granted by Ministry of Education of China (under Project Number 3191004).

Author information

Authors and Affiliations

  1. School of Information Science and Technology, Sun Yat-sen University, Guangzhou, 510006, China

    Yunong Zhang, Xiaotian Yu, Dongsheng Guo, Yonghua Yin & Zhijun Zhang

Authors
  1. Yunong Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiaotian Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Dongsheng Guo
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yonghua Yin
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Zhijun Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yunong Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Y., Yu, X., Guo, D. et al. Weights and structure determination of multiple-input feed-forward neural network activated by Chebyshev polynomials of Class 2 via cross-validation. Neural Comput & Applic 25, 1761–1770 (2014). https://doi.org/10.1007/s00521-014-1667-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-014-1667-0

Keywords