Abstract
This paper presents an effective method to control the state of charge (SOC) of energy storage system (ESS) installed in a microgrid (MG). Considering voltage and frequency variations after islanding occurrence and based on the stability criteria, MG pre-islanding conditions are divided into secure and insecure classes. It is shown that insecure MG can become secure, if appropriate value for SOC of the ESS is chosen in different conditions of the MG. To select the most important variables of MG, which can estimate proper values of the SOC, a feature selection procedure known as RELIEF is used in this paper. Among all the MG variables, critical ones are selected. Using them, appropriate value of the SOC can be calculated for different conditions of the MG. This approach is economic because it does not change the result of optimal power flow (OPF). In some conditions, the proper control of SOC cannot solely make the MG secure. In these conditions, DGs generated power should be also changed to make the MG secure. This condition leads to a violation from OPF solution and increases the cost of operation. The results demonstrate the effectiveness of the proposed method in comparison with other methods.









Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Xiong X, Ouyang J (2011) Modeling and transient behavior analysis of an inverter-based microgrid. Electr Power Compon Syst 40(1):112–130
Majumder R, Chakrabarti S, Ledwich G, Ghosh A (2013) Advanced battery storage control for an autonomous microgrid. Electr Power Compon Syst 41(2):157–181
Sanjari MJ, Gharehpetian GB (2013) Small signal stability based fuzzy potential function proposal for secondary frequency and voltage control of islanded microgrid. Electr Power Compon Syst 41(5):485–499
Johnson B, Davoudi A, Chapman P, Sauer P (2011) A unified dynamic characterization framework for microgrid systems. Electr Power Compon Syst 40(1):93–111
Majumder R, Ghosh A, Ledwich G, Zare F (2010) Power management and power flow control with back-to-back converters in a utility connected microgrid. IEEE Trans Power Syst 25(2):821–834
Piagi P, Lasseter R (2006) Autonomous control of microgrids. In: Power engineering society general meeting, 2006. IEEE, p 8
Peças Lopes JA, Moreira CL, Madureira AG (2006) Defining control strategies for microgrids islanded operation. IEEE Trans Power Syst 21(2):916–924
Katiraei F, Iravani MR (2006) Power management strategies for a microgrid with multiple distributed generation units. IEEE Trans Power Syst 21(4):1821–1831
Moreira CL, Pecas Lopes JA (2007) Microgrids dynamic security assessment. In: International conference on clean electrical power, ICCEP ‘07, pp 26–32
Pogaku N, Prodanovic M, Green TC (2007) Modeling, analysis and testing of autonomous operation of an inverter-based microgrid. IEEE Trans Power Electron 22(2):613–625
Katiraei F, Iravani MR, Lehn PW (2007) Small-signal dynamic model of a micro-grid including conventional and electronically interfaced distributed resources. IET Gener Transm Distrib 1(3):369–378
Karapidakis ES, Hatziargyriou ND (2002) Online preventive dynamic security of isolated power systems using decision trees. IEEE Trans Power Syst 17(2):297–304
Vasconcelos H, Peças Lopes JA (2006) ANN design for fast security evaluation of interconnected systems with large wind power production. In: Proceedings of PMAPS 2006—the 9th international conference on probabilistic methods applied to power systems, 11–15 June 2006, Stockholm, Sweden
Fidalgo JN, Peças Lopes JA, Miranda V (1996) Neural networks applied to preventive control measures for the dynamic security of isolated power systems with renewable. IEEE Trans Power Syst 11(4):1811–1816
Kononenko I (1994) Estimating attributes: analysis and extension of relief. In: Proceedings of the European conference on machine learning, pp 171–182
Sikonja M, Kononenko I (2003) Theoretical and empirical analysis of ReliefF and RRelief. Mach Learn 53(1–2):23–69
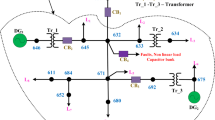
Papathanassiou S, Hatziargyriou N, Strunz K (2005) A benchmark low voltage microgrid network. In: Proceedings of the CIGRE symposium power systems with dispersed generation, April 2005, Athens
Levron Y, Guerrero JM, Beck Y (2013) Optimal power flow in microgrids with energy storage. IEEE Trans Power Syst 99:1–9
Pandey SN, Pandey NK, Tapaswi S, Srivastava L (2010) Neural network-based approach for ATC estimation using distributed computing. IEEE Trans Power Syst 25(3):1291–1300
Kang MS, Chen CS, Ke YL, Lin CH (2007) Load profile synthesis and wind power generation prediction for an isolated power system. IEEE Trans Ind Appl 43(6):1459–1464
Changsong C, Shanxu D, Tao C, Bangyin L (2009) Energy trading model for optimal microgrid scheduling based on genetic algorithm. In: IEEE 6th international power electronics and motion control conference (IPEMC ‘09), Yin Jinjun, pp 2136–2139
Sanjari MJ, Gharehpetian GB (2014) Incomplete information based decentralized cooperative control strategy for distributed energy resources of VSI-based microgrids. Neural Comput Appl 25(1):189–197
Sanjari MJ, Gharehpetian GB (2014) Game theoretic approach to cooperative control of distributed energy resources in islanded microgrid considering voltage and frequency stability. Neural Comput Appl 25(2):343–351
Zhang Y, Song S, Zhang H, Wu C, Yin W (2012) A hybrid genetic algorithm for two-stage multi-item inventory system with stochastic demand. Neural Comput Appl 21(6):1087–1098
Wang G, Guo L, Wang H, Duan H, Liu L, Li J (2014) Incorporating mutation scheme into krill herd algorithm for global numerical optimization. Neural Comput Appl 24(3–4):853–871
Sanjari MJ, Alizadeh Mousavi O, Gharehpetian GB (2013) Assessing the risk of blackout in the power system including HVDC and FACTS devices. Int Trans Electr Energy Syst 23(1):109–121
Yilmaz S, Bilgin MZ (2013) Modeling and simulation of injection control system on a four-stroke type diesel engine development platform using artificial neural networks. Neural Comput Appl 22(7–8):1713–1725
Pachón-García FT, Jiménez-Barco A, Paniagua-Sánchez JM, Rufo-Pérez M (2014) New approach based on ANN and RBF for analyzing the spatial distribution of electromagnetic field from an exposure standpoint. Neural Comput Appl. doi:10.1007/s00521-014-1638-5
Smrekar J, Pandit D, Fast M, Assadi M, De S (2010) Prediction of power output of a coal-fired power plant by artificial neural network. Neural Comput Appl 19(5):725–740
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
-
(a)
Voltage controller The DAEs of voltage controller are as follows [10, 11]:
$$ \dot{\phi }_{\text{d}} = v_{\text{od,ref}} - v_{\text{od}} $$(8)$$ \dot{\phi }_{\text{q}} = v_{{{\text{oq}},{\text{ref}}}} - v_{\text{oq}} $$(9)$$ i_{\text{ld}}^{*} = F \cdot i_{\text{od}} - \omega_{\text{n}} \cdot C_{\text{f}} \cdot v_{\text{oq}} + k_{\text{pv}} \left( {v_{\text{od}}^{*} - v_{\text{od}} } \right)( - v_{\text{od}} ) + k_{\text{iv}} \cdot \phi_{\text{d}} $$(10)$$ i_{\text{iq}}^{*} = F \cdot i_{\text{oq}} - \omega_{\text{n}} \cdot C_{\text{f}} \cdot v_{\text{od}} + k_{\text{pv}} \left( {v_{\text{oq}}^{*} - v_{\text{oq}} } \right) + k_{\text{iv}} \cdot \phi_{\text{q}} $$(11)where φ d and φ q are the state variable corresponding to voltage PI controller.
-
(b)
Current controller The DAEs of current controller are as follows [10, 11]:
$$ \dot{\gamma }_{\text{d}} = i_{\text{id}}^{*} - i_{\text{id}} $$(12)$$ \dot{\gamma }_{\text{q}} = i_{\text{iq}}^{*} - i_{\text{iq}} $$(13)$$ v_{\text{id}}^{*} = - \omega_{\text{n}} \cdot L_{\text{f}} \cdot i_{\text{lq}} + k_{\text{pc}} \left( {i_{\text{lq}}^{*} - i_{\text{lq}} } \right) + k_{\text{ic}} \cdot \gamma_{\text{d}} $$(14)$$ v_{\text{iq}}^{*} = \omega_{\text{n}} \cdot L_{\text{f}} \cdot i_{\text{ld}} + k_{\text{pc}} \left( {i_{\text{lq}}^{*} - i_{\text{lq}} } \right) + k_{\text{ic}} \cdot \gamma_{\text{q}} $$(15)where γ d and γ q are the state variable corresponding to current PI controller.
-
(c)
Switching process [10] demonstrates that when the DC voltage is fixed, the switching process can be neglected and the inverter produces the reference voltage (v i = v i*). In this condition, the dynamic of primary source has no effect on VSC output voltage. As shown in [10, 11], the fixed DC voltage needs the fast-response energy storage in each VSC.
-
(d)
Output filter and coupling inductance The DAE of output filter and coupling inductance are as follows [10]:
$$ \dot{i}_{\text{ld}} = - \frac{{r_{\text{f}} }}{{L_{\text{f}} }}i_{\text{ld}} + \omega_{\text{ref}} i_{\text{lq}} + \frac{1}{{L_{\text{f}} }}v_{\text{id}} - \frac{1}{{L_{\text{f}} }}v_{\text{od}} $$(16)$$ \dot{i}_{\text{lq}} = - \frac{{r_{\text{f}} }}{{L_{\text{f}} }}i_{\text{lq}} - \omega_{\text{ref}} i_{\text{ld}} + \frac{1}{{L_{\text{f}} }}v_{\text{iq}} - \frac{1}{{L_{\text{f}} }}v_{\text{oq}} $$(17)$$ \dot{v}_{\text{od}} = \omega_{\text{ref}} v_{\text{oq}} + \frac{1}{{C_{\text{f}} }}i_{\text{ld}} - \frac{1}{{C_{\text{f}} }}i_{\text{od}} $$(18)$$ \dot{v}_{\text{oq}} = - \omega_{\text{ref}} v_{\text{od}} + \frac{1}{{C_{\text{f}} }}i_{\text{lq}} - \frac{1}{{C_{\text{f}} }}i_{\text{oq}} $$(19)$$ \dot{i}_{\text{od}} = - \frac{{r_{\text{c}} }}{{L_{\text{c}} }}i_{\text{od}} + \omega_{\text{ref}} i_{\text{oq}} + \frac{1}{{L_{\text{c}} }}v_{\text{od}} - \frac{1}{{L_{\text{c}} }}v_{\text{bd}} $$(20)$$ \dot{i}_{\text{oq}} = - \frac{{r_{\text{c}} }}{{L_{\text{c}} }}i_{\text{oq}} - \omega_{\text{ref}} i_{\text{od}} + \frac{1}{{L_{\text{c}} }}v_{\text{oq}} - \frac{1}{{L_{\text{c}} }}v_{\text{bq}} $$(21)where i ld and i lq are the direct and quadratic components of filter current, respectively, and other parameters are shown in Fig. 2.
-
(e)
Load modeling Although many types of load can exist in MGs, a general RL load is considered in this paper. The state equations of the RL load connected at ith node are as follows:
$$ \frac{{{\text{d}}(i_{{{\text{load}}\,D,i}} )}}{{{\text{d}}t}} = \frac{{ - R_{{{\text{load}}\,i}} }}{{L_{{{\text{load}}\,i}} }}i_{{{\text{load}}\,D,i}} + \omega i_{{{\text{load}}\,Q,i}} + \frac{1}{{L_{{{\text{load}}\,i}} }}v_{bDi} $$(22)$$ \frac{{{\text{d}}(i_{{{\text{load}}\,Q,i}} )}}{{{\text{d}}t}} = \frac{{ - R_{{{\text{load}}\,i}} }}{{L_{{{\text{load}}\,i}} }}i_{{{\text{load}}\,Q,i}} - \omega i_{{{\text{load}}\,D,i}} + \frac{1}{{L_{{{\text{load}}\,i}} }}v_{bQi} $$(23) -
(f)
Network modeling In a common reference frame, the state equations of line current of i-th line connected between nodes j and k are as follows:
$$ \frac{{{\text{d}}(i_{{{\text{line}}\,D,i}} )}}{{{\text{d}}t}} = \frac{{ - R_{{{\text{line}}\,i}} }}{{L_{{{\text{line}}\,i}} }}i_{{{\text{line}}\,D,i}} + \omega ii_{{{\text{line}}\,Q,i}} + \frac{1}{{L_{{{\text{line}}\,i}} }}v_{bDi} - \frac{1}{{L_{{{\text{line}}\,i}} }}v_{bDk} $$(24)$$ \frac{{{\text{d}}(i_{{{\text{line}}\,Q,i}} )}}{{{\text{d}}t}} = \frac{{ - R_{{{\text{line}}\,i}} }}{{L_{{{\text{line}}\,i}} }}i_{{{\text{line}}\,Q,i}} - \omega ii_{{{\text{line}}\,D,i}} + \frac{1}{{L_{{{\text{line}}\,i}} }}v_{bQi} - \frac{1}{{L_{{{\text{line}}\,i}} }}v_{bQk} $$(25)
Rights and permissions
About this article
Cite this article
Khomami Pamsari, H., Seyed-Shenava, SJ. & Shayeghi, H. State of charge preventive control of storage device to stabilize VSI-based microgrid after islanding occurrence using ANN-based control. Neural Comput & Applic 26, 669–677 (2015). https://doi.org/10.1007/s00521-014-1715-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-014-1715-9