Batch gradient training method with smoothing $\boldsymbol{\ell}_{\bf 0}$ regularization for feedforward neural networks

Abstract

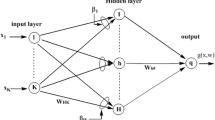
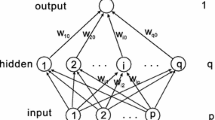
This paper considers the batch gradient method with the smoothing $\ell _0$ regularization (BGSL0) for training and pruning feedforward neural networks. We show why BGSL0 can produce sparse weights, which are crucial for pruning networks. We prove both the weak convergence and strong convergence of BGSL0 under mild conditions. The decreasing monotonicity of the error functions during the training process is also obtained. Two examples are given to substantiate the theoretical analysis and to show the better sparsity of BGSL0 than three typical $\ell _p$ regularization methods.

Appendix

In this “Appendix”, we give the proof of Theorem 1. For simplicity, we introduce the following notation:

$$\begin{aligned} {\bf F}^{n,j}={\bf F}({\bf V}^{n}\varvec{\xi }^j), \end{aligned}$$

(21)

for $n=1,2,\ldots,$ and $j=1,\ldots,J.$

Lemma 1

Suppose the Assumptions (A1)–(A3) are valid, then $E_{\bf w} ({\bf w})$ satisfies Lipschitz condition, that is, there exists a positive constant $C_2$, such that

$$\begin{aligned} \Vert E_{\bf w} ({\bf w}^{n+1} )-E_{\bf w} ({\bf w}^{n} )\Vert \le C_2\Vert {\bf w}^{n+1}-{\bf w}{^n}\Vert . \end{aligned}$$

(22)

Specially, for $\theta \geqslant 0$ , we have

$$\begin{aligned} \Vert E_{\bf w} ({\bf w}^{n}+\theta ({\bf w}^{n+1}-{\bf w}^{n}) )-E_{\bf w} ({\bf w}^{n} )\Vert \le C_2 \theta \Vert {\bf w}^{n+1}-{\bf w}^{n}\Vert . \end{aligned}$$

(23)

Proof

Using (12a) and the triangular inequality we have

$$\begin{aligned}&\Vert E_{{\bf w}_0} ({\bf w}^{n+1} )-E_{{\bf w}_0} ({\bf w}^{n} )\Vert \\&\quad =\left\| \sum \limits _{j=1}^J(e_j'({\bf w}_0^{n+1}\cdot {\bf F}^{n+1,j}){\bf F}^{n+1,j}-e_j'({\bf w}_0^{n}\cdot {\bf F}^{n,j}){\bf F}^{n,j})+\lambda (H_{\sigma }'({\bf w}_0^{n+1})-H_{\sigma }'({\bf w}_0^{n}))\right\| \\&\quad \le \sum \limits _{j=1}^J\Vert e_j'({\bf w}_0^{n+1}\cdot {\bf F}^{n+1,j}){\bf F}^{n+1,j}-e_j'({\bf w}_0^{n}\cdot {\bf F}^{n,j}){\bf F}^{n,j}\Vert +\lambda \Vert H_{\sigma }'({\bf w}_0^{n+1})-H_{\sigma }'({\bf w}_0^{n})\Vert . \end{aligned}$$

(24)

In order to give a further estimation of the above equation, we consider the change of ${\bf F}^{n,j}$ defined in (21) between two steps:

$$\begin{aligned} \Vert {\bf F}^{n+1,j}-{\bf F}^{n,j}\Vert&= \left\| \left( \begin{array}{c} f({\bf w}_1^{n+1}\cdot \varvec{\xi } ^j)-f({\bf w}_1^{n}\cdot \varvec{\xi } ^j) \\ \vdots \\ f({\bf w}_L^{n+1}\cdot \varvec{\xi } ^j)-f({\bf w}_L^{n}\cdot \varvec{\xi } ^j)\end{array}\right) \right\| \\&= \left\| \left( \begin{array}{c} f'(t_1)({\bf w}_1^{n+1}-{\bf w}_1^{n})\cdot \varvec{\xi } ^j\\ \vdots \\ f'(t_L)({\bf w}_L^{n+1}-{\bf w}_L^{n})\cdot \varvec{\xi } ^j\end{array}\right) \right\| \\&\le C_{3}\sum \limits _{l=1}^{L}\Vert {\bf w}^{n+1}_l-{\bf w}^{n}_l\Vert, \end{aligned}$$

(25)

where $t_l$ lies on the segment between ${\bf w}_l^{n+1}\cdot \varvec{\xi }^j$ and ${\bf w}_l^{n}\cdot \varvec{\xi }^j$, for $l=1,\ldots, L$, and $C_3=\sup f'(t)\max \limits _{1\le j\le J}\Vert \varvec{\xi }^j\Vert$.

It is easy to see that $e_j'({\bf w}_0^{n}\cdot {\bf F}^{n,j})$ is Lipschitz continuous and let the positive constant $C_4$ be the corresponding Lipschitz constant. Using (25), Assumption (A1) and the Cauchy–Schwartz inequality, we have

$$\begin{aligned}&\Vert e_j'({\bf w}_0^{n+1}\cdot {\bf F}^{n+1,j}){\bf F}^{n+1,j}-e_j'({\bf w}_0^{n}\cdot {\bf F}^{n,j}){\bf F}^{n,j}\Vert \\&\quad \le |e_j'({\bf w}_0^{n+1}\cdot {\bf F}^{n+1,j})-e_j'({\bf w}_0^{n}\cdot {\bf F}^{n,j})|\Vert {\bf F}^{n+1,j}\Vert +|e_j'({\bf w}_0^{n}\cdot {\bf F}^{n,j})|\Vert {\bf F}^{n+1,j}-{\bf F}^{n,j}\Vert \\&\quad \le C_4\Vert {\bf F}^{n+1,j}\Vert |{\bf w}_0^{n+1}\cdot {\bf F}^{n+1,j}-{\bf w}_0^{n}\cdot {\bf F}^{n,j}| +|e_j'({\bf w}_0^{n}\cdot {\bf F}^{n,j})|\Vert {\bf F}^{n+1,j}-{\bf F}^{n,j}\Vert \\&\quad \le C_4\Vert {\bf F}^{n+1,j}\Vert ^2 \Vert {\bf w}_0^{n+1}-{\bf w}_0^{n}\Vert +(C_4\Vert {\bf F}^{n+1,j}\Vert \Vert {\bf w}_0^{n}\Vert +|e_j'({\bf w}_0^{n}\cdot {\bf F}^{n,j})|)\Vert {\bf F}^{n+1,j}-{\bf F}^{n,j}\Vert \\&\quad \le C_4\Vert {\bf F}^{n+1,j}\Vert ^2 \Vert {\bf w}_0^{n+1}-{\bf w}_0^{n}\Vert +C_{5}\sum \limits _{l=1}^{L}\Vert {\bf w}^{n+1}_l-{\bf w}^{n}_l\Vert \\&\quad \le C_6 \Vert {\bf w}^{n+1}-{\bf w}{^n}\Vert, \end{aligned}$$

(26)

with

$$\begin{aligned} C_{5}&= C_3\sup (C_4\Vert {\bf F}^{n+1,j}\Vert \Vert {\bf w}_0^{n}\Vert +|e_j'({\bf w}_0^{n}\cdot {\bf F}^{n,j})|),\\ C_6&= \sqrt{L+1}\max \{ C_4\sup \Vert {\bf F}^{n+1,j}\Vert ^2,C_5\}. \end{aligned}$$

Similar to the deduction of (25), using the definition of $H_{\sigma }^{\prime }(\cdot )$, Assumption (A3) and the mean value theorem, we have

$$\begin{aligned} \Vert H_{\sigma }'({\bf w}_0^{n+1})-H_{\sigma }'({\bf w}_0^{n})\Vert&= \left\| \left( \begin{array}{c} h_{\sigma }'(w_{01}^{n+1})-h_{\sigma }'(w_{01}^{n})\\ \vdots \\ h_{\sigma }'(w_{0L}^{n+1})-h_{\sigma }'(w_{0L}^{n})\end{array} \right) \right\| \\&\le C_7 \Vert {\bf w}_{0}^{n+1}-{\bf w}_{0}^{n}\Vert, \end{aligned}$$

(27)

where $C_7=\sup h_{\sigma }^{\prime \prime }(t)$.

Combing the above Eqs. (24), (26), and (27), we have

$$\begin{aligned} \Vert E_{{\bf w}_0} ({\bf w}^{n+1} )-E_{{\bf w}_0} ({\bf w}^{n} )\Vert \le JC_6 \Vert {\bf w}^{n+1}-{\bf w}{^n}\Vert +\lambda C_7 \Vert {\bf w}_{0}^{n+1}-{\bf w}_{0}^{n}\Vert . \end{aligned}$$

(28)

Similarly, for $l=1,\ldots,L$, there exits a constant $C_8$, such that

$$\begin{aligned} \Vert E_{{\bf w}_l} ({\bf w}^{n+1} )-E_{{\bf w}_l} ({\bf w}^{n} )\Vert \le J C_8 \Vert {\bf w}^{n+1}-{\bf w}{^n}\Vert + \lambda C_7 \Vert {\bf w}_{l}^{n+1}-{\bf w}_{l}^{n}\Vert . \end{aligned}$$

(29)

Then, Eqs. (10), (11), (28) and (29) validate (22):

$$\begin{aligned} \Vert E_{\bf w} ({\bf w}^{n+1} )-E_{\bf w} ({\bf w}^{n} )\Vert \le C_2 \Vert {\bf w}^{n+1}-{\bf w}{^n}\Vert, \end{aligned}$$

(30)

where $C_2=J\sqrt{C_6^2+LC_8^2}+\lambda C_7$.

Equation (23) is naturally valid as a simple application of (22). $\square$

Now, we proceed to the proof of Theorem 1 by dealing with Eqs.  (16)–(19) separately.

Proof of (16)

By the differential mean value theorem, there exists a constant $\theta \in [0,1]$, such that

$$\begin{aligned} E({\bf w}^{n+1})- E({\bf w}^n)&= (E_{\bf w} ({\bf w}^{n}+\theta ({\bf w}^{n+1}-{\bf w}^{n}) ))^T({\bf w}^{n+1}- {\bf w}^n) \\&= (E_{\bf w} ({\bf w}^{n}))^T({\bf w}^{n+1}- {\bf w}^n) \\&\quad +\,(E_{\bf w} ({\bf w}^{n} +\theta ({\bf w}^{n+1}-{\bf w}^{n}) )-(E_{\bf w} ({\bf w}^{n})))^T({\bf w}^{n+1}- {\bf w}^n) \\& \le -\,\eta \Vert E_{\bf w} ({\bf w}^{n})\Vert ^2+C_2\theta \Vert {\bf w}^{n+1}- {\bf w}^n\Vert ^2 \\&\le \,(-\eta +C_2\eta ^2)\Vert E_{\bf w} ({\bf w}^{n})\Vert ^2. \end{aligned}$$

(31)

To make (16) valid, we only require the learning rate $\eta$ to satisfy

$$\begin{aligned} 0<\eta <\frac{1}{C_2}. \end{aligned}$$

(32)

$\square$

Proof of (17)

Equation (17) is directly obtained by (16) and $E({\bf w}^n)>0(n=1,2,\ldots )$.$\square$

Proof of (18)

Let $\beta =\eta -C_2\eta ^2$. By (31), we have

$$\begin{aligned} E({\bf w}^{n+1})&\le E({\bf w}^n)-\beta \Vert E_{\bf w} ({\bf w}^{n})\Vert ^2 \\&\le \ldots \le E({\bf w}^{0})-\beta \sum \limits _{t=0}^n\Vert E_{\bf w} ({\bf w}^{t})\Vert ^2. \end{aligned}$$

(33)

Considering $E({\bf w}^{n+1})>0$, let $n\rightarrow \infty$, then we have

$$\begin{aligned} \beta \sum \limits _{t=0}^{\infty }\Vert E_{\bf w} ({\bf w}^{t})\Vert ^2\le E({\bf w}^{0})<\infty . \end{aligned}$$

(34)

This immediately gives

$$\begin{aligned} \mathop {\hbox {lim}}\limits _{n\rightarrow \infty }\Vert {E_{\bf w}({\bf w}^n)}\Vert =0. \end{aligned}$$

(35)

$\square$

To prove (19), we need the following lemma.

Lemma 2

(See Lemma 3 in [23]) Let $F:\Upphi \subset {\mathbb {R}}^k\rightarrow {\mathbb {R}},(k\ge 1)$ be continuous for a bounded closed region $\Upphi$ , and $\Upphi _0=\{{\bf z}\in \Upphi :F({\bf z})=0\}$ . The projection of $\Upphi _0$ on each coordinate axis does not contain any interior point. Let the sequence $\{{\bf z}^n\}$ satisfy:

• (i) $\hbox {lim}_{n\rightarrow \infty }F({\bf z}^n)=0$;

• (ii) $\hbox {lim}_{n\rightarrow \infty }\Vert {\bf z}^{n+1}-{\bf z}^n\Vert =0$.

Then, there exists a unique ${\bf z}^*\in \Upphi_0$ such that $\mathop {\hbox {lim}}\limits _{n\rightarrow \infty }{\bf z}^n={\bf z}^*.$

Proof of (19)

Obviously $\Vert E_{\bf w} ({\bf w})\Vert$ is a continuous function under Assumptions $(A2)$ and $(A3)$. Using (13) and (18), we have

$$\begin{aligned} \mathop {\hbox {lim}}\limits _{n\rightarrow \infty }\Vert {\bf w}^{n+1}-{\bf w}^n\Vert =\eta \mathop {\hbox {lim}}\limits _{n\rightarrow \infty }\Vert {E_{\bf w}({\bf w}^n)}\Vert =0. \end{aligned}$$

(36)

Furthermore, Assumption (A4) is valid. Thus, applying Lemma 2, there exists a unique ${\bf w}^{*}\in \Upphi$ such that $\mathop {\hbox {lim}}\limits _{n\rightarrow \infty }{\bf w}^n={\bf w}^{*}$. $\square$