Skip to main content

Advertisement

Springer Nature Link
Log in

Artificial neural network method for solving the Navier–Stokes equations

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

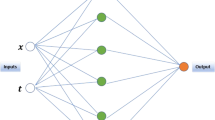
In this paper, a new method based on neural network is developed for obtaining the solution of the Navier–Stokes equations in an analytical function form. The solution procedure is based upon forming a trial solution consisting of two parts. The first part directly satisfies the boundary conditions and therefore, contains no adjustable parameters. The second part is constructed such that the governing equation is satisfied inside the solution domain, while the boundary conditions remain untouched. This part involves a feed-forward neural network, containing adjustable parameters (the weights), which must be determined such that the resulting approximate error function is minimized. The details of the method are discussed, and the capabilities of the method are illustrated by solving Navier–Stokes problem with different boundary conditions. The performance of the method and the accuracy of the results are evaluated by comparing with the available numerical and analytical solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Christiano V, Smarandache F (2008) An exact mapping from Navier–Stokes equation to Schrodinger equation via Riccati equation. Prog Phys 1:38–39

    MathSciNet  Google Scholar 

  2. Dongyang S, Jincheng R et al (2009) A new second order nonconforming mixed finite element scheme for the stationary Stokes and Navier–Stokes equations. Appl Math Comput 207:462–477

    Article  MATH  MathSciNet  Google Scholar 

  3. Effati S, pakdaman M (2010) Artificial neural network approach for solving fuzzy differential equations. Inf Sci 180:1434–1457

    Article  MATH  MathSciNet  Google Scholar 

  4. Erdogan ME, Imrak CE (2009) An analytical solution of the Navier–Stokes equation for flow over a moving plate bounded by two side walls. J Mech Eng 55(12):749–754

  5. Hayati M, Karami B (2007) Feed forward neural network for solving partial differential equations. J Appl Sci 7(19):2812–2817

    Article  Google Scholar 

  6. Horiuchi K, Dutta P et al (2007) Electro osmosis with step changes in zeta potential in microchannels. AIChE J 53(10):2521–2533

    Article  Google Scholar 

  7. Largris IE, Likas A et al (1998) Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans Neural Netw 9(5):987–1000

    Article  Google Scholar 

  8. Mohyuddin M et al (2008) Exact solutions of time-dependent Navier–Stokes equations by hodograph–Legendre transformation method. Tamsui Oxf J Math Sci 24(3):257–268

    MATH  MathSciNet  Google Scholar 

  9. Odibat Z, Momani S (2006) Analytical spherically symmetric solution for the time-fractional Navier–Stokes equation. Adv Theor Appl Math 1(2):97–107

    MATH  MathSciNet  Google Scholar 

  10. Zhang J, Liu F et al (2006) Electro-osmotic flow and mixing in heterogeneous microchannels. Phys Rev E 73:056305–056312

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Quchan University of Advanced Technology, Quchan, Iran

    M. Baymani

  2. Department of Mathematics, Ferdowsi University of Mashhad, Mashhad, Iran

    S. Effati & A. Kerayechian

  3. Mechanical Engineering Department, Faculty of Engineering, Ferdowsi University of Mashhad, Mashhad, Iran

    H. Niazmand

  4. The Center of Excellence on Soft Computing and Intelligent Information Processing (SCIP), Ferdowsi University of Mashhad, Mashhad, Iran

    S. Effati

Authors
  1. M. Baymani
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. S. Effati
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. H. Niazmand
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. A. Kerayechian
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to S. Effati.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Baymani, M., Effati, S., Niazmand, H. et al. Artificial neural network method for solving the Navier–Stokes equations. Neural Comput & Applic 26, 765–773 (2015). https://doi.org/10.1007/s00521-014-1762-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-014-1762-2

Keywords