Skip to main content
Springer Nature Link
Log in

Stability of Markovian jump neural networks with mode-dependent delays and generally incomplete transition probability

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

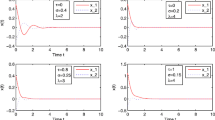
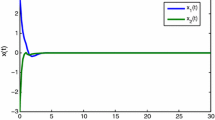
This paper deals with the robust exponential stability problem for a class of Markovian jump neural networks with mode-dependent delays and generally incomplete transition probability. The delays vary randomly depending on the mode of the networks. Each transition rate can be completely unknown, or only its estimate value is known. By using a new Lyapunov–Krasovskii functional, a delay-dependent stability criterion is presented in terms of linear matrix inequalities (LMIs). The proposed LMI results extend the earlier publications. Finally, a numerical example is given to show the effectiveness and efficiency of the results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Dehyadegary L, Seyyedsalehi SA, Nejadgholi I (2011) Nonlinear enhancement of noisy speech, using continuous attractor dynamics formed in recurrent neural networks. Neurocomputing 74(17):2716–2724

    Article  Google Scholar 

  2. Ryeu JK, Chung HS (1996) Chaotic recurrent neural networks and their application to speech recognition. Neurocomputing 13(2–4):281–294

    Article  Google Scholar 

  3. Galn CO, Prez JRR, Corts SG, Snchez AB (2013) Analysis of the influence of forestry environments on the accuracy of GPS measurements by means of recurrent neural networks. Math Comput Model 57(7–8):2016–2023

    Article  Google Scholar 

  4. Murray JC, Erwin HR, Wermter S (2009) Robotic sound-source localisation architecture using cross-correlation and recurrent neural networks. Neural Netw 22(2):173–189

    Article  Google Scholar 

  5. Zhang M, Chu Z (2012) Adaptive sliding mode control based on local recurrent neural networks for underwater robot. Ocean Eng 45:56–62

    Article  MATH  Google Scholar 

  6. Haykin S (1995) Recurrent neural networks for adaptive filtering. Control Dyn Syst 68:89–119

    Article  Google Scholar 

  7. Subrahmanya N, Shin YC (2010) Constructive training of recurrent neural networks using hybrid optimization. Neurocomputing 73(13–15):2624–2631

    Article  Google Scholar 

  8. Al Seyab RK, Cao Y (2008) Nonlinear system identification for predictive control using continuous time recurrent neural networks and automatic differentiation. J Process Control 18(6):568–581

    Article  Google Scholar 

  9. van den Driessche P, Zou X (1998) Global attractivity in delayed Hopfield neural network models. SIAM J Appl Math 58(6):1878–1890

    Article  MathSciNet  MATH  Google Scholar 

  10. Wu A, Wen S, Zeng Z (2012) Synchronization control of a class of memristor-based recurrent neural networks. Inf Sci 183(1):106–116

    Article  MathSciNet  MATH  Google Scholar 

  11. Samli R, Arik S (2009) New results for global stability of a class of neutral-type neural systems with time delays. Appl Math Comput 210(2):564–570

    Article  MathSciNet  MATH  Google Scholar 

  12. Ensari T, Arik S (2010) New results for robust stability of dynamical neural networks with discrete time delays. Expert Syst Appl 37(8):5925–5930

    Article  Google Scholar 

  13. Faydasicok O, Arik S (2013) A new robust stability criterion for dynamical neural networks with multiple time delays. Neurocomputing 99(1):290–297

    Article  Google Scholar 

  14. Senan S, Arik S, Liu D (2012) New robust stability results for bidirectional associative memory neural networks with multiple time delays. Appl Math Comput 218(23):11472–11482

    Article  MathSciNet  MATH  Google Scholar 

  15. Arik S (2005) Global robust stability analysis of neural networks with discrete time delays. Chaos Solitons Fractals 26(5):1407–1414

    Article  MathSciNet  MATH  Google Scholar 

  16. Wang Z, Shu H, Fang J, Liu X (2006) Robust stability for stochastic Hopfield neural networks with time delays. Nonlinear Anal Real World Appl 7:1119–1128

    Article  MathSciNet  MATH  Google Scholar 

  17. Wang Z, Fang J, Liu X (2008) Global stability of stochastic high-order neural networks with discrete and distributed delays. Chaos Solitons Fractals 36:388–396

    Article  MathSciNet  MATH  Google Scholar 

  18. Kao Y, Wang C (2013) Global stability analysis for stochastic coupled reaction-diffusion systems on networks. Nonlinear Anal B Real World Appl 14(3):1457–1465

    Article  MathSciNet  MATH  Google Scholar 

  19. Wang C, Kao Y, Yang G (2012) Exponential stability of impulsive stochastic fuzzy reaction-diffusion Cohen–Grossberg neural networks with mixed delays. Neurocomputing 89:55–63

    Article  Google Scholar 

  20. Kao Y, Guo J, Wang C, Sun X (2012) Delay-dependent robust exponential stability of Markovian jumping reaction-diffusion Cohen–Grossberg neural networks with mixed delays. J Franklin Inst 349(6):1972–1988

    Article  MathSciNet  Google Scholar 

  21. Kao Y, Wang C, Zhang L (2013) Delay-dependent exponential stability of impulsive Markovian jumping Cohen–Grossberg neural networks with reaction-diffusion and mixed delays. Neural Process Lett 38(3):321–346

    Article  Google Scholar 

  22. Han W, Liu Y, Wang L (2010) Robust exponential stability of Markovian jumping neural networks with mode-dependent delay. Commun Nonlinear Sci Numer Simul 15(9):2529–2535

    Article  MathSciNet  MATH  Google Scholar 

  23. Liu Y (2009) Stochastic asymptotic stability of Markovian jumping neural networks with Markov mode estimation and mode-dependent delays. Phys Lett A 373(41):3741–3742

    Article  MathSciNet  MATH  Google Scholar 

  24. Sun M, Lam J, Xu S, Zou Y (2007) Robust exponential stabilization for Markovian jump systems with mode-dependent input delay. Automatica 43:1799–1807

    Article  MathSciNet  MATH  Google Scholar 

  25. Xu S, Chen T, Lam J (2003) Robust \(H_\infty \) filtering for uncertain Markovian jump systems with mode-dependent time delays. IEEE Trans Autom Control 48(5):900–906

    Article  MathSciNet  Google Scholar 

  26. Wang Z, Liu Y, Yu L, Liu X (2006) Exponential stability of delayed recurrent neural networks with Markovian jumping parameters. Phys Lett A 356:346–352

    Article  MATH  Google Scholar 

  27. Kao Y, Xie J, Wang C (2014) Stabilisation of singular Markovian jump systems with generally uncertain transition rates. IEEE Trans Autom Control 59(9):2604–2610

    Article  MathSciNet  Google Scholar 

  28. Boyd S, Ghaoui LE, Feron E, Balakrishnan V (1994) Linear matrix inequalities in system and control theory. SIAM, Philadelphia

    Book  MATH  Google Scholar 

  29. Gu K (2000) An integral inequality in the stability problem of time-delay systems. 39th IEEE conference on decision and control, Sydney, Australia, vol 11, pp 2805–2810

Download references

Acknowledgments

The authors would like to thank the editors and the anonymous reviewers for their valuable comments and constructive suggestions. This research is supported by the National Natural Science Foundations of China (61473097).

Author information

Authors and Affiliations

  1. School of Science, Harbin Institute of Technology, Weihai, 264209, China

    Jing Xie & Yonggui Kao

  2. College of Information Science and Engineering, Ocean University of China, Qingdao, 266100, China

    Jing Xie

Authors
  1. Jing Xie
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yonggui Kao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yonggui Kao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xie, J., Kao, Y. Stability of Markovian jump neural networks with mode-dependent delays and generally incomplete transition probability. Neural Comput & Applic 26, 1537–1553 (2015). https://doi.org/10.1007/s00521-014-1812-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-014-1812-9

Keywords