Abstract
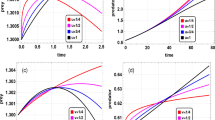
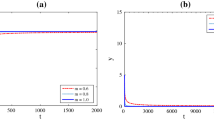
In recent years, prey–predator models appearing in various fields of mathematical biology have been proposed and studied extensively due to their universal existence and importance. The paper presents the solutions of time-fractional Lotka–Volterra models with the help of analytical method of nonlinear problem called homotopy perturbation method (HPM). By using initial values, the explicit solutions of time-fractional prey and predator populations for different particular cases have been derived. The numerical solutions show that only a few iterations are needed to obtain accurate approximate solutions. The dynamic behavior of the system investigated from the point of view of local stability. We also carry out a detailed analysis on stability of equilibrium.



Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
He JH (1999) Homotopy perturbation technique. Comput Methods Appl Mech Eng 178:257–262
He JH (2000) A Coupling method of homotopy technique and perturbation technique for nonlinear problem. Int J Nonlinear Mech 35(1):37–43
He JH (2004) Comparison of homotopy perturbation method and homotopy analysis method. Appl Math Comput 156:527–539
Yan LM (2013) Modified homotopy perturbation method coupled with Laplace transform for fractional heat transfer and porous media equations. Therm Sci 17(5):1409–1414
He JH (2006) New interpretation of homotopy perturbation method. Int J Mod Phys B 20:2561–2568
He JH (2006) Some asymptotic methods for strongly nonlinear equations. Int J Mod Phys B 20:1141–1199
Saadatmandia A, Dehghan M, Eftekharia A (2009) Application of He’s homotopy perturbation method for non-linear system of second-order boundary value problems. Nonlinear Anal Real World Appl 10:1912–1922
Shakeri F, Dehghan M (2007) Numerical solution of a biological population model using He’s variational iteration method. Comput Math Appl 54:1197–1209
Dehghan M, Nasri M, Razvan MR (2007) Global stability of a deterministic model for HIV infection in vivo. Chaos, Solitons Fractals 34:1225–1238
Shakeri F, Dehghan M (2008) Solution of a model describing biological species living together using the variational iteration method. Math Comput Model 48:685–699
Dehghan M, Salehi R (2010) Solution of a nonlinear time-delay model in biology via semi-analytical approaches. Comput Phys Commun 181:1255–1265
Shakeri F, Dehghan M (2011) The finite volume spectral element method to solve Turing models in the biological pattern formation. Comput Math Appl 2:4322–4336
Pamuk S, Pamuk N (2010) He’s homotopy perturbation method for continuous population models for single and interacting species. Comput Math Appl 59:612–621
Hassan HN, El-Tawil MA (2012) Series solution for continuous population models for single and interacting species by the homotopy analysis method. Commun Numer Anal cna-00106:21
Rafei M, Ganji DD, Danili H (2007) Solution of the epidemic model by homotopy perturbation method. Appl Math Comput 187:1056–1062
Podlubny I (1999) Fractional differential equation. Academic Press, New York
Samko SG, Kilbas AA, Marichev OI (2002) Fractional integrals and derivatives: theory and applications. Taylor and Francis, London
Murray JD (1993) Mathematical biology I. An introduction. Springer, Berlin
He JH (2014) A tutorial review on fractal space time and fractional calculus. Int J Theor Phys 53(11):3698–3718
Saha Ray S (2008) An application of the modified decomposition method for the solution of coupled Klein–Gordon–Schrödinger equation. Commun Nonlinear Sci Numer Simul 13(7):1311–1317
Jafari H, Ghasempour S, Khalique CM (2013) A comparison between adomian’s polynomials and He’s polynomials for nonlinear functional equations. Math Probl Eng 943232:4
Jafari H, Ghasempour S, Khalique CM (2013) Comments on “He’s homotopy perturbation method for calculating Adomian polynomials”. Int J Nonlinear Sci Numer Simul 14(6):339–343
Cai L, Li X, Ghosh M, Guo B (2009) Stability analysis of an HIV/AIDS epidemic model with treatment. J Comput Appl Math 229:313–323
Driessche PV, Watmough J (2002) Reproducing numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci 180:29–48
Das S, Gupta PK (2011) A mathematical model on fractional Lotka–Volterra equations. J Thoer Biol 277:1–6
Kuttler C (2009) Mathematical models in biology II. http://www-m6.ma.tum.de/~kuttler/script_current.pdf
Acknowledgments
This research work was financially supported by BRNS of Bhabha Atomic Research Centre, Mumbai under Department of Atomic Energy, Government of India vide Grant No. 2012/37P/54/BRNS/2382.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Saha Ray, S., Sahoo, S. A class of time-fractional-order continuous population models for interacting species with stability analysis. Neural Comput & Applic 26, 1495–1504 (2015). https://doi.org/10.1007/s00521-014-1816-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-014-1816-5