Skip to main content

Advertisement

Springer Nature Link
Log in

Exponential stability of inertial BAM neural networks with time-varying delay via periodically intermittent control

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

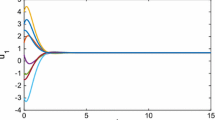
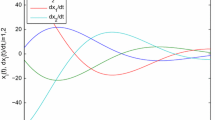
In this paper, we study global exponential stability problem for inertial BAM neural networks with time-varying delay via periodically intermittent control. By utilizing suitable variable substitution, the second-order system can be transformed into first-order differential equations. It is shown that the states of the inertial BAM neural networks with time-varying delay via periodically intermittent control can be globally exponential stabilized with a desired oribis under the designed intermittent controller. Finally, a typical example is chosen to illustrate the validation of the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Wen SP, Zeng ZG, Huang TW (2012) H\(\infty \) Filtering for neutral systems with mixed delays and multiplicative noises. IEEE Trans Circuits Syst Part II 59(11):820–824

    Article  Google Scholar 

  2. Li XD, Song S (2014) Research on synchronization of chaotic delayed neural networks with stochastic perturbation using impulsive control method. Commun Nonlinear Sci Numer Simul 19(10):3892–3900

    Article  MathSciNet  Google Scholar 

  3. Li XD, Song S (2013) Impulsive control for existence, uniqueness, and global stability of periodic solutions of recurrent neural networks with discrete and continuously distributed delays. IEEE Trans Neural Netw Learn Syst 24(6):868–877

    Article  Google Scholar 

  4. Wen SP, Bao G, Zeng ZG, Chen YR, Huang TW (2013) Global exponential synchronization of memristor-based recurrent networks with time-varying delays. Neural Netw 48:195–203

    Article  MATH  Google Scholar 

  5. Hopfield J (1984) Neurons with graded response have collective computational properties like those of two-stage neurons. In: Proceedings of the national academy science United States America, vol 81, no. 10, pp 3088–3092

  6. Chua L, Yang L (1988) Cellular neural networks: applications. IEEE Trans Circuits Syst 35(10):1273–1290

    Article  MathSciNet  Google Scholar 

  7. Chua L, Yang L (1988) Cellular networks: theory. IEEE Trans Circuits Syst 35(10):1257–1272

    Article  MathSciNet  MATH  Google Scholar 

  8. Cohen M, Grossberg S (1983) Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans Syst Man Cybern 13(5):815–826

    Article  MathSciNet  MATH  Google Scholar 

  9. Wen SP, Zeng ZG, Huang TW (2013) Passivity analysis of memristor-based recurrent neural networks with time-varying delays. J Frankl Inst 350:2354–2370

    Article  MathSciNet  MATH  Google Scholar 

  10. Kosko B (1988) Bi-directional associative memories. IEEE Trans Syst Man Cybern 18(1):49–60

    Article  MathSciNet  Google Scholar 

  11. He X, Li CD, Huang TW (2014) Neural network for solving convex quadratic bilevel programming problems. Neural Netw 51:17–25

    Article  Google Scholar 

  12. He X, Li CD, Huang TW (2014) A recurrent neural network for solving bilevel linear programming problem. IEEE Trans Neural Netw Learn Syst 25(4):824–830

    Article  Google Scholar 

  13. Tang Y, Wang Z, Gao H, Swift S, Kurths J (2012) a constrained evolutionary computation method for detecting controlling regions of cortical networks. IEEE/ACM Trans Comput Biol Bioinf 9(6):1569–1581

    Article  Google Scholar 

  14. Strogatz SH, Stewart I (1993) Coupled oscillators and biological synchronization. Sci Am 269(6):102–9

    Article  Google Scholar 

  15. Wu CW (2007) Synchronization in complex networks of nonlinear dynamical systems. World Scientific, Singapore

    Book  MATH  Google Scholar 

  16. Gao Q, Feng G, Xi ZY (2014) A new design of robust h sliding mode control for uncertain stochasti T-S fuzzy time-delay systems. IEEE Trans Cybern 44(9):1556–1566

    Article  Google Scholar 

  17. Yang XS, Cao JD, Lu JQ (2011) synchronization of delayed complex dynamical networks with impulsive and stochastic effects. Nonlinear Anal Real World Appl 12:2252–2266

    Article  MathSciNet  MATH  Google Scholar 

  18. Cao JD, Wan Y (2014) Matrix measure strategies for stability and synchronization of inertial BAM neural network with time delays. Neural Netw 53:165–172

    Article  Google Scholar 

  19. Wei X (2013) Exponential stability of periodic solutions for inertial Cohen–Grossberg-type BAM neural networks with time delays. WSEAS Trans Math 12(2):159–169

    Google Scholar 

  20. Xu C, Zhang Q (2014) Existence and global exponential stability of anti-periodic solutions for BAM neural networks with inertial term and delay. Neurocomputing 153:108–116

    Article  Google Scholar 

  21. Hu J, Cao J, Alofi A et al (2014) Pinning synchronization of coupled inertial delayed neural networks. Cogn Neurodyn. doi:10.1007/s11571-9322-0

    Google Scholar 

  22. Żochowski M (2000) Intermittent dynamical control. Phys D Nonlinear Phenom 145(3):181–190

    Article  MATH  Google Scholar 

  23. Cai SM, Liu ZR, Xu FD, Shen JW (2009) Periodically intermittent controlling complex dynamical networks with time-varying delays to a desired orbit. Phys Lett A 373:3846–3854

    Article  MathSciNet  MATH  Google Scholar 

  24. Yu J, Hu C, Jiang HJ, Teng ZD (2012) Exponential lay synchronization for delayed fuzzy cellular nerual networks via periodically intermittent control. Math Comput Simul 82:895–908

    Article  MathSciNet  MATH  Google Scholar 

  25. Xia WG, Cao JD (2009) Pinning synchronization of delayed dynamical networks via periodically intermittent control. Chaos 19:012120

    Article  MathSciNet  Google Scholar 

  26. Wang JY, Feng JW, Xu C, Zhao Y (2013) Exponential synchronization of stochastic perturbed complex networks with time-varying delays via periodically intermittent pinning. Commun Nonlinear Sci Numer Simul 18:3146–3157

    Article  MathSciNet  Google Scholar 

  27. Halanay A (1966) Differential equation: stability. Oscillations, time lags. Academic, New York

    MATH  Google Scholar 

  28. Xia W, Cao J (2009) Pinning synchronization of delayed dynamical networks via periodically intermittent control. Chaos Interdiscip J Nonlinear Sci 19(1):013120

    Article  MathSciNet  Google Scholar 

  29. Yang Z, Xu D (2007) stability analysis and design of impulsive control systems with time delay. IEEE Trans Autom Control 52(8):1448–1454

    Article  Google Scholar 

Download references

Acknowledgments

This publication was made possible by NPRP Grant \(\sharp \) NPRP 4-1162-1-181 from the Qatar National Research Fund (a member of Qatar Foundation). The statements made herein are solely the responsibility of the authors. This work was also supported by Natural Science Foundation of China (Grant Nos: 61374078, 61403313).

Author information

Authors and Affiliations

  1. College of Computer Science, Chongqing University, Chongqing, 400044, People’s Republic of China

    Wei Zhang & Chuandong Li

  2. Department of Mathematics, Texas A&M University at Qatar, P.O. Box 23874, Doha, Qatar

    Tingwen Huang

  3. College of Mathematics and Physics, Chongqing University of Science and Technology, Chongqing, 401331, People’s Republic of China

    Jie Tan

Authors
  1. Wei Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Chuandong Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Tingwen Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jie Tan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Chuandong Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, W., Li, C., Huang, T. et al. Exponential stability of inertial BAM neural networks with time-varying delay via periodically intermittent control. Neural Comput & Applic 26, 1781–1787 (2015). https://doi.org/10.1007/s00521-015-1838-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-015-1838-7

Keywords