Skip to main content

Advertisement

Springer Nature Link
Log in

Artificial neural network training utilizing the smooth variable structure filter estimation strategy

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

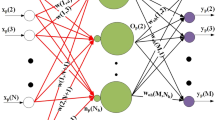
A multilayered neural network is a multi-input, multi-output nonlinear system in which network weights can be trained by using parameter estimation algorithms. In this paper, a novel training method is proposed. This method is based on the relatively new smooth variable structure filter (SVSF) and is formulated for feed-forward multilayer perceptron training. The SVSF is a state and parameter estimation that is based on the sliding mode concept and works in a predictor–corrector fashion. The SVSF training performance is tested on three benchmark pattern classification problems. Furthermore, a study is presented comparing the popular back-propagation method, the extended Kalman filter, and the SVSF.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Notes

  1. Data are available for download through (ics.ci.edu, directory/pub/machine-learning-database).

  2. There are 16 missing values for attribute (input) 6, and they are replaced by a constant value of 0.3 instead for network training.

  3. The datasets involve zero elements that might be replacing some missing attributes.

References

  1. Runxuan Z (2005) Efficient sequential and batch learning artificial neural network methods for classification problems. Ph.D. Thesis, Nanyang Technological University, Singapore

  2. Warner B, Misra M (1996) Understanding neural networks as statistical tools. Am Stat 50:284–293

    Google Scholar 

  3. Cybenko GV (1989) Approximation by superpositions of a sigmoidal function. Math Control Signals Syst 2:303–314

    Article  MathSciNet  MATH  Google Scholar 

  4. Patuwo E, Hu MY, Hung MS (1993) Two-group classification using neural networks. Decis Sci 24:825–845

    Article  Google Scholar 

  5. Teixeira RA, Baraga AD, Menezes BD (2000) Control of a robotic manipulator using artificial neural networks with on-line adaptation. J Neural Process 12(1):19–31

    Article  MATH  Google Scholar 

  6. Werbos P (1990) Backpropagation through time: what it does and how to do it. Proc IEEE 78:1550–1560

    Article  Google Scholar 

  7. Haykin S (2007) Neural networks—a comprehensive foundation, 3rd edn. Prentice Hall, Englewood Cliffs, NJ

    MATH  Google Scholar 

  8. Haykin S (2001) Kalman filtering and neural networks, 3rd edn. Prentice Hall, Englewood Cliffs, NJ

    Book  Google Scholar 

  9. Saarinen S, Bramley R, Cybenko G (1991) The numerical solution of neural-network training problems, CRSD report 1089. Center for Supercomputing Research and Development, University Illinois, Urbana, IL

  10. Zhou G, Si J (1998) Advanced neural-network training algorithm with reduced complexity based on Jacobian deficiency. IEEE Trans Neural Netw 9(3):448–453

    Article  Google Scholar 

  11. Hagen MT, Menhaj MB (1994) Training feedforward networks with the Marquardt algorithm. IEEE Trans Neural Networks 5:989–993

    Article  Google Scholar 

  12. Watrous RL (1987) Learning algorithms for connectionist networks: applied gradient methods of nonlinear optimization. In: IEEE conference on neural networks, vol 2, pp 619–627

  13. Setiono R, Hui LCK (1995) Use of a quasi-Newton method in a feedforward neural network construction algorithm. IEEE Trans Neural Netw 6:273–277

    Article  Google Scholar 

  14. Heimes F (1998) Extended Kalman filter neural network training: experimental results and algorithm improvements. In: Proceedings of the IEEE conference on systems, man, and cybernetics, vol 2, pp 1639–1644

  15. Haykin S (2001) Kalman filtering and neural networks, ISBNs: 0-471-36998-5; 0-471-22154-6 ed

  16. Singhal S, Wu L (1989) Training multilayer perceptrons with the extended Kalman algorithm. Adv Neural Inf Process Syst 1:133–140

    Google Scholar 

  17. Puskorius G, Feldkamp L (1991) Decoupled extended Kalman filter training of feedforward layered networks. In: Proceedings of the IJCNNÕ91 I, Seattle, pp 771–777

  18. Williams R (1992) Training recurrent networks using the extended Kalman filter. In: Proceedings of the IJCNN’92 IV, pp 241–246

  19. Sun P, Kenneth M (1998) Training recurrent neural networks for very high performance with the extended Kalman algorithm. Intell Eng Syst Through Artif Neural Netw 8:121–126

    Google Scholar 

  20. Deng X, Jianying X, Guo W, Liu J (2005) A new learning algorithm for diagonal recurrent neural network. In: First international conference on natural computation

  21. Feldkamp L, Feldkamp T, Prokhorov D (2001) Neural network training with the nprKF. In: Proceedings of the international joint conference on neural networks

  22. Wan EA, van der Merwe R (2000) The unscented Kalman filter for nonlinear estimation. In: Proceedings of the IEEE adaptive systems for signal processing, communications, and control symposium

  23. Julier SJ, Uhlmann J, Durrant-Whyte HF (1995) A new approach for filtering nonlinear systems. In: Proceedings of the American control conference

  24. Habibi SR (2007) The smooth variable structure filter. Proc IEEE 95(5):1026–1059

    Article  MathSciNet  Google Scholar 

  25. Habibi SR, Burton R Parameter identification for a high-performance hydrostatic actuation system using the variable structure filter concept. J Dyn Syst Meas Control Trans ASME 129(2):229–235

  26. Wang S, Burton R, Habibi SR (2007) A smooth variable structure filter for state estimation. Control Intell Syst 35(4):386–393

    MathSciNet  MATH  Google Scholar 

  27. Gadsden SA, Habibi SR (2009) Target tracking using the smooth variable structure filter. In: ASME dynamic systems and control conference (DSCC)

  28. Gadsden SA, Habibi SR (2010) A new form of the smooth variable structure filter with a covariance derivation. In: IEEE conference on decision and control, Atlanta, Georgia

  29. Ahmed R, El Sayed M, Andrew Gadsden, JTASH (2013) Fault detection of an engine using a neural network trained by the smooth variable structure filter. In: IEEE Journal of Vehicular Technology

  30. Prechelt L (1994) PROBEN1—a set of neural network benchmark problems and benchmarking rules. Technical Report, Karlsruhe, Germany

  31. Iiguni Y, Sakai H, Tokumaru H (1992) A real-time learning algorithm for a multilayered neural network based on the extended Kalman filter. IEEE Trans Signal Process 40(4):659–966

    Article  Google Scholar 

  32. Anderson BDO, Moore JB (1979) Optimal filtering. Prentice-Hall, Englewood Cliffs, NJ

    MATH  Google Scholar 

  33. Trebaticky P, Jiri P (2008) Neural network training with extended Kalman filter using graphics processing unit. In: ICANN

  34. Le Yang YX (2006) Development of a new recurrent neural network toolbox. In: A Course Project Report on Training Recurrent Multilayer Perceptron and Echo State Network

  35. Singhal S, Wu L (1989) Training multilayer perceptrons with the extended Kalman algorithm. Adv Neural Inf Process Syst 133–140

  36. Feldkamp L, Puskorius G (1998) A signal processing framework based on dynamic networks with application to problems in adaptation, filtering, and classification. In: IEEE

  37. Feldkamp LA, Puskorius GV (1994) Training controllers for robustness: multi-stream DEKF. In: IEEE international conference on neural networks, Orlando

  38. Feldkamp LA, Puskorius GV (1994) Training of robust neurocontrollers. In: IEEE international conference on decision and control, Orlando

  39. Gadsden SA, Habibi SR (2013) A new robust filtering strategy for linear systems. ASME J Dyn Syst Meas Control 135(1):014503-1-9

  40. Gadsden SA, Song Y, Habibi SR (2013) Novel model-based estimators for the purposes of fault detection and diagnosis. IEEE/ASME Trans Mechatron 18(4):1237–1249

    Article  Google Scholar 

  41. Habibi SR, Burton R (2003) The variable structure filter. J Dyn Syst Meas Control (ASME) 125:287–293

    Article  Google Scholar 

  42. Habibi SR, Burton R (2007) Parameter identification for a high performance hydrostatic actuation system using the variable structure filter concept. ASME J Dyn Syst Meas Control 129(2). doi:10.1115/1.2431816

  43. Ahmed R, El Sayed M, Gadsden SA, Habibi SR, Tjong J (2015) Engine fault detection and classification using artificial neural network techniques. IEEE Trans Veh Technol 64(1):21–33

    Article  Google Scholar 

  44. Gadsden SA (2011) Smooth variable structure filtering: theory and applications. Hamilton, Ontario

    Google Scholar 

  45. Wolberg WH. Cancer dataset: Wiliams H. Wolberg, Center for machine learning and intelligent systems. University of California, Irvine

  46. Heinke D, Hamker F (1998) Comparing neural networks: a benchmark on growing neural gas, growing cell structures, and fuzzy ARTMAP. IEEE Trans Neural Netw 9:1279–1291

    Article  Google Scholar 

  47. Rumelhart DE, Hinton GE, Williams RJ, Rumelhart DE, McClelland J (1986) Learning internal representations by error propagation, vol 1. MIT Press, Cambridge, MA, pp 318–362

    Google Scholar 

  48. Hagan MT, Demuth HB, Beale MH (2002) Neural network design. Natick, MA

  49. Levenberg K (1944) A method for the solution of certain problems in least squares. Q Appl Math 2:164–168

    MathSciNet  MATH  Google Scholar 

  50. Marquardt D (1963) An algorithm for least-squares estimation of nonlinear parameters. SIAM J Appl Math 11:431–441

    Article  MathSciNet  MATH  Google Scholar 

  51. Dennis J, Schnabel R (1983) Numerical methods for unconstrained optimization and nonlinear equations. Prentice-Hall, Englewood Cliffs, NJ

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, McMaster University, Hamilton, ON, Canada

    Ryan Ahmed, Mohammed El Sayed & Saeid Habibi

  2. Department of Mechanical Engineering, University of Maryland, Baltimore County, Baltimore, MD, USA

    S. Andrew Gadsden

  3. Ford Canada, Windsor, ON, Canada

    Jimi Tjong

Authors
  1. Ryan Ahmed
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mohammed El Sayed
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. S. Andrew Gadsden
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jimi Tjong
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Saeid Habibi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to S. Andrew Gadsden.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahmed, R., El Sayed, M., Gadsden, S.A. et al. Artificial neural network training utilizing the smooth variable structure filter estimation strategy. Neural Comput & Applic 27, 537–548 (2016). https://doi.org/10.1007/s00521-015-1875-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-015-1875-2

Keywords