Skip to main content

Advertisement

Springer Nature Link
Log in

Finite-time stability criteria for a class of fractional-order neural networks with delay

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

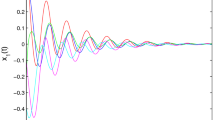
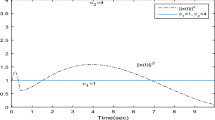
Finite-time stabilities of a class of fractional-order neural networks delayed systems with order \(\alpha {:}\) \(0<\alpha \le 0.5\) and \(0.5<\alpha <1\) are addressed in this paper, respectively. By using inequality technique, two new delay-dependent sufficient conditions ensuring stability of such fractional-order neural networks over a finite-time interval are obtained. Obtained conditions are less conservative than that given in the earlier references. Two numerical examples are given to show the effectiveness of our proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Rakkiyappan R, Chandrasekar A, Lakshmanan S, Park J, Jung H (2013) Effects of leakage time-varying delays in Markovian jump neural networks with impulse control. Neurocomputing 121:365–378

    Article  Google Scholar 

  2. Rakkiyappan R, Chandrasekar A, Lakshmanan S, Park J (2014) Exponential stability of Markovian jumping stochastic Cohen–Grossberg neural networks with mode-dependent probabilistic time-varying delays and impulses. Neurocomputing 131:265–277

    Article  Google Scholar 

  3. Li T, Wang T, Song A, Fei S (2013) Combined convex technique on delay-dependent stability for delayed neural networks. IEEE Trans Neural Netw Learn Syst 24(9):1459–1466

    Article  Google Scholar 

  4. Wang X, Li C, Huang T, Duan S (2014) Global exponential stability of a class of memristive neural networks with time-varying delays. Neural Comput Appl 24(7–8):1707–1715

    Article  Google Scholar 

  5. Rakkiyappan R, Zhu Q, Chandrasekar A (2014) Stability of stochastic neural networks of neutral type with markovian jumping parameters: A delay fractioning approach. J Franklin Inst 351(3):1553–1570

    Article  MathSciNet  Google Scholar 

  6. Xiao M, Zheng W, Cao J (2013) Bifurcation and control in a neural network with small and large delays. Neural Netw 44:132–142

    Article  MATH  Google Scholar 

  7. Lundstrom B, Higgs M, Spain W, Fairhall A (2008) Fractional differentiation by neocortical pyramidal neurons. Nat Neurosci 11:1335–1342

    Article  Google Scholar 

  8. Anastasio T (1994) The fractional-order dynamics of brainstem vestibulooculomotor neurons. Biol Cybern 72:69–79

    Article  Google Scholar 

  9. Anastassiou G (2012) Fractional neural network approximation. Comput Math Appl 64(6):1655–1676

    Article  MathSciNet  MATH  Google Scholar 

  10. Boroomand A, Menhaj M (2009) Fractional-order Hopfield neural networks. Lecture Notes in Computer Science 5506:883–890

  11. Arena P, Fortua L, Porto D (2000) Chaotic behavior in noninteger-order cellular neural networks. Phys Rev E 61:776–781

    Article  Google Scholar 

  12. Liu L, Liu C, Liang D (2013) Hyperchaotic behavior in arbitrary-dimensional fractional-order quantum cellular neural network model. Int J Bifurc Chaos 23(3):1350044

    Article  MathSciNet  MATH  Google Scholar 

  13. Kaslik E, Sivasundaram S (2012) Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw 32:245–256

    Article  MATH  Google Scholar 

  14. Huang X, Zhao Z, Wang Z, Li Y (2012) Chaos and hyperchaos in fractional-order cellular neural networks. Neurocomputing 94:13–21

    Article  Google Scholar 

  15. Wu R, Hei X, Chen L (2013) Finite-time stability of fractional-order neural networks with delay. Commun Theor Phys 60(2):189–193

    Article  MathSciNet  MATH  Google Scholar 

  16. Chen L, Chai Y, Wu R, Ma T, Zhai H (2013) Dynamic analysis of a class of fractional-order neural networks with delay. Neurocomputing 111:190–194

    Article  Google Scholar 

  17. Alofi A, Cao J, Elaiw A, Al-Mazrooei A (2014) Delay-dependent stability criterion of Caputo fractional neural networks with distributed delay. Discret Dyn Nat Soc, 529358

  18. Chen L, Qu J, Chai Y, Wu R, Qi G (2013) Synchronization of a class of fractional-order chaotic neural networks. Entropy 15(8):3265–3276

    Article  MathSciNet  Google Scholar 

  19. Zhou S, Hua L, Zhua Z (2008) Chaos control and synchronization in a fractional neuron network system. Chaos Solitons Fractals 36(4):973–984

    Article  MathSciNet  MATH  Google Scholar 

  20. Chen J, Zeng Z, Jiang P (2014) Global Mittag–Leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Netw 51:1–8

    Article  MATH  Google Scholar 

  21. Dorato P (1961) Short time stability in linear time-varying systems. In: Proceedings of IRE international convention record part 4:83–87

  22. Zhang X (2008) Some results of linear fractional order time-delay system. Appl Math Comput 197:407–411

    MathSciNet  MATH  Google Scholar 

  23. Lazarevic M, Spasic A (2009) Finite-time stability analysis of fractional order time-delay systems: Gronwall’s approach. Math Comput Model 49(3–4):475–481

    Article  MathSciNet  MATH  Google Scholar 

  24. Lazarevic M, Debeljkovic D (2005) Finite time stability analysis of linear autonomous fractional order systems with delayed state. Asian J Control 7(4):440–447

    Article  MathSciNet  Google Scholar 

  25. Lazarevic M (2006) Finite time stability analysis of PD\(^\alpha \) fractional control of robotic time-delay systems. Mech Res Commun 33(2):269–279

    Article  MathSciNet  MATH  Google Scholar 

  26. Aghababa M (2014) A Lyapunov-based control scheme for robust stabilization of fractional chaotic systems. Nonlinear Dyn 78:2129C2140

    Article  MathSciNet  Google Scholar 

  27. Roohi M, Aghababa M, Haghighi A (2014) Switching adaptive controllers to control fractional-order complex systems with unknown structure and input nonlinearities. Complexity. doi:10.1002/cplx.21598

    Google Scholar 

  28. Aghababa M (2014) Synchronization and stabilization of fractional second-order nonlinear complex systems. Nonlinear Dyn. doi:10.1007/s11071-014-1411-4

  29. Aghababa M (2014) Fractional modeling and control of a complex nonlinear energy supply-demand system. Complexity. doi:10.1002/cplx.21533

    Google Scholar 

  30. Haghighi A, Aghababa M, Roohi M (2014) Robust stabilization of a class of three-dimensional uncertain fractional-order non-autonomous systems. Int J Ind Math 6(2):133–139

    Google Scholar 

  31. Aghababa M (2014) Control of fractional-order systems using chatter-free sliding mode approach. J Comput Nonlinear Dyn 9(3):031003

    Article  Google Scholar 

  32. Aghababa M (2014) A switching fractional calculus-based controller for normal non-linear dynamical systems. Nonlinear Dyn 75(3):577–588

    Article  MathSciNet  MATH  Google Scholar 

  33. Aghababa M (2014) Control of nonlinear non-integer-order systems using variable structure control theory. Trans Inst Measure Control 36(3):425–432

    Article  Google Scholar 

  34. Aghababa M (2013) No-chatter variable structure control for fractional nonlinear complex systems. Nonlinear Dyn 73(4):2329–2342

    Article  MathSciNet  MATH  Google Scholar 

  35. Aghababa M (2013) Design of a chatter-free terminal sliding mode controller for nonlinear fractional-order dynamical systems. Int J Control 86:1744–1756

    Article  MathSciNet  MATH  Google Scholar 

  36. Aghababa M (2013) A novel terminal sliding mode controller for a class of non-autonomous fractional-order systems. Nonlinear Dyn 73(1–2):679–688

    Article  MathSciNet  MATH  Google Scholar 

  37. Aghababa M (2012) Finite-time chaos control and synchronization of fractional-order nonautonomous chaotic (hyperchaotic) systems using fractional nonsingular terminal sliding mode technique. Nonlinear Dyn 69(1–2):247–261

    Article  MathSciNet  MATH  Google Scholar 

  38. Aghababa M (2012) Robust stabilization and synchronization of a class of fractional-order chaotic systems via a novel fractional sliding mode controller. Commun Nonlinear Sci Numer Simul 17:2670–2681

    Article  MathSciNet  MATH  Google Scholar 

  39. Chen Y, Ahn H, Podlubny I (2007) Robust stability test of a class of linear time-invariant interval fractional-order system using Lyapunov inequality. Appl Math Comput 187(1):27–34

    MathSciNet  MATH  Google Scholar 

  40. Moornani K, Mohammad H (2009) On robust stability of linear time invariant fractional-order systems with real parametric uncertainties. ISA Trans 48(4):484–490

    Article  Google Scholar 

  41. Lim Y, Oh K, Ahn H (2013) Stability and stabilization of fractional-order linear systems subject to input saturation. IEEE Trans Autom Control 58(4):1062–1067

    Article  MathSciNet  Google Scholar 

  42. Deng W, Li C, Lu J (2007) Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn 48(4):409–416

    Article  MathSciNet  MATH  Google Scholar 

  43. Sadati S, Baleanu D, Ranjbar A, Ghaderi R, Abdeljawad T (2010) Mittag–Leffler stability theorem for fractional nonlinear systems with delay. Abstr Appl Anal, 108651

  44. Li C, Deng W (2007) Remarks on fractional derivatives. Appl Math Comput 187(2):777–784

    MathSciNet  MATH  Google Scholar 

  45. Mitrinovic D (1970) Analytic inequalities. Springer, Berlin

    Book  MATH  Google Scholar 

  46. Willett D (1964) Nonlinear vector integral equations as contraction mappings. Arch Ration Mech Anal 15:79–86

    Article  MathSciNet  MATH  Google Scholar 

  47. Cao J (1999) Global stability analysis in delayed cellular neural networks. Phys Rev E 59:5940–5944

    Article  MathSciNet  Google Scholar 

  48. Yang X, Song Q, Liu Y, Zhao Z (2014) Finite-time stability analysis of fractional-order neural networks with delay. Neurocomputing. doi:10.1016/j.neucom.2014.11.023i

    Google Scholar 

  49. Ke Y, Miao C (2014) Stability analysis of fractional-order CohenCGrossberg neural networks with time delay. Int J Comput Math. doi:10.1080/00207160.2014.935734

  50. Wu R, Lu Y, Chen L (2015) Finite-time stability of fractional delayed neural networks. Neurocomputing 149:700–707

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported by the National Natural Science Funds of China for Distinguished Young Scholar under Grant (No. 50925727), the National Natural Science Foundation of China (Nos. 61403115, 61374135), the National Defense Advanced Research Project Grant (Nos. C1120110004, 9140 A27020211DZ5102) and the Key Grant Project of Chinese Ministry of Education under Grant (No. 313018).

Author information

Authors and Affiliations

  1. School of Electrical Engineering and Automation, Hefei University of Technology, Hefei, 230009, China

    Liping Chen, Cong Liu & Yigang He

  2. School of Mathematics, Anhui University, Hefei, 230039, China

    Ranchao Wu

  3. School of Automation, Chongqing University, Chongqing, 400044, China

    Yi Chai

Authors
  1. Liping Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Cong Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ranchao Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yigang He
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Yi Chai
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Liping Chen.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, L., Liu, C., Wu, R. et al. Finite-time stability criteria for a class of fractional-order neural networks with delay. Neural Comput & Applic 27, 549–556 (2016). https://doi.org/10.1007/s00521-015-1876-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-015-1876-1

Keywords