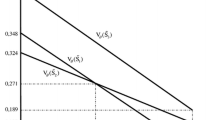
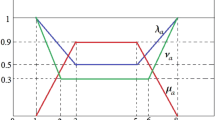
Abstract
In this paper, a novel outranking approach for multi-criteria decision-making (MCDM) problems is proposed to address situations where there is a set of numbers in the real unit interval and not just a specific number with a neutrosophic set. Firstly, the operations of interval neutrosophic sets and their related properties are introduced. Then some outranking relations for interval neutrosophic numbers (INNs) are defined based on ELECTRE IV, and the properties of the outranking relations are further discussed in detail. Additionally, based on the outranking relations of INNs, a ranking approach is developed in order to solve MCDM problems. Finally, two practical examples are provided to illustrate the practicality and effectiveness of the proposed approach. Moreover, a comparison analysis based on the same examples is also conducted.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–356
Zadeh LA (1968) Probability measures of fuzzy events. J Math Anal Appl 23:421–427
Turksen IB (1986) Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst 20:191–210
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Atanassov KT (2000) Two theorems for intuitionistic fuzzy sets. Fuzzy Sets Syst 110:267–269
Gau WL, Buehrer DJ (1993) Vague sets. IEEE Trans Syst Man Cybern 23:610–614
Bustince H, Burillo P (1996) Vague sets are intuitionistic fuzzy sets. Fuzzy Sets Syst 79:403–405
Liu HW, Wang GJ (2007) Multi-criteria methods based on intuitionistic fuzzy sets. Eur J Oper Res 179:220–233
Zhi P, Li Z (2012) A novel approach to multi-attribute decision making based on intuitionistic fuzzy sets. Expert Syst Appl 39:2560–2566
Zeng SZ, Su WH (2011) Intuitionistic fuzzy ordered weighted distance operator. Knowl Based Syst 24(8):1224–1232
Shinoj TK, Sunil JJ (2012) Intuitionistic fuzzy multisets and its application in medical diagnosis. Int J Math Comput Sci 6:34–37
Sotirov S, Sotirova E, Orozova D (2009) Neural network for defining intuitionistic fuzzy sets in e-learning. NIFS 15:33–36
Guo Y, Sengur A (2014) NECM: neutrosophic evidential c-means clustering algorithm. Neural Comput Appl. doi:10.1007/s00521-014-1648-3
Chaira T (2011) A novel intuitionistic fuzzy C means clustering algorithm and its application to medical images. Appl Soft Comput 11:1711–1717
Joshi BP, Kumar S (2012) Fuzzy time series model based on intuitionistic fuzzy sets for empirical research in stock market. Int J Appl Evol Comput 3:71–84
Atanassov KT, Gargov G (1989) Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst 31:343–349
Wang J-Q, Nie R, Zhang H-Y, Chen X-H (2013) New operators on triangular intuitionistic fuzzy numbers and their applications in system fault analysis. Inf Sci 251:79–95
Torra V (2010) Hesitant fuzzy sets. Int J Intell Syst 25:529–539
Torra V, Narukawa Y (2009). On hesitant fuzzy sets and decision. In: Proceedings of the 18th IEEE international conference on fuzzy systems, Jeju Island, Korea, pp 1378–1382
Wang J-Q, Wu J-T, Wang J, Zhang H-Y, Chen X-H (2014) Interval-valued hesitant fuzzy linguistic sets and their applications in multi-criteria decision-making problems. Inf Sci 288:55–72
Wang J, Zhou P, Li K, Zhang H, Chen X (2014) Multi-criteria decision-making method based on normal intuitionistic fuzzy-induced generalized aggregation operator. TOP 22:1103–1122
Wang J, Wu J, Wnag J, Zhang H, Chen X (2015) Multi-criteria decision-making methods based on the Hausdorff distance of hesitant fuzzy linguistic numbers. Soft Comput. doi:10.1007/s00500-015-1609-5
Wang J-Q, Peng J-J, Zhang H-Y, Liu T, Chen X-H (2015) An uncertain linguistic multi-criteria group decision-making method based on a cloud model. Group Decis Negot 24(1):171–192
Wei G (2010) Some induced geometric aggregation operators with intuitionistic fuzzy information and their application to group decision making. Appl Soft Comput 10(2):423–431
Wang H, Smarandache F, Zhang YQ, Sunderraman R (2010) Single valued neutrosophic sets. Multisp Multistruct 4:410–413
Smarandache F (1999) A unifying field in logics. Neutrosophy: neutrosophic probability, set and logic. American Research Press, Rehoboth
Smarandache F (2003) A unifying field in logics neutrosophic logic. Neutrosophy, neutrosophic set, neutrosophic probability. American Research Press, Rehoboth
Rivieccio U (2008) Neutrosophic logics: prospects and problems. Fuzzy Sets Syst 159(14):1860–1868
Majumdarar P, Samant SK (2014) On similarity and entropy of neutrosophic sets. J Intell Fuzzy Syst 26:1245–1252
Ye J (2014) Single valued neutrosophic cross-entropy for multicriteria decision making problems. Appl Math Model 38(3):1170–1175
Ye J (2014) A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. J Intell Fuzzy Syst 26:2459–2466
Liu P, Wang Y (2014) Multiple attribute decision-making method based on single-valued neutrosophic normalized weighted Bonferroni mean. Neural Comput Appl. doi:10.1007/s00521-014-1688-8
Peng J-J, Wang J-Q, Wang J, Zhang H-Y, Chen X-H (2015) Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. Int J Syst Sci. doi:10.1080/00207721.2014.994050
Wang H, Smarandache F, Zhang Y-Q, Sunderraman R (2005) Interval neutrosophic sets and logic: theory and applications in computing. Hexis, Arizona
Lupiáñez FG (2009) Interval neutrosophic sets and topology. Kybernetes 38(3/4):621–624
Broumi S, Smarandache F (2015) New Operations on Interval Neutrosophic Sets. Journal of New Theory 1:24–37
Broumi S, Smarandache F (2013) Correlation coefficient of interval neutrosophic set. Appl Mech Mater 436:511–517
Broumi S, Smarandache F (2014) Cosine similarity measure of interval valued neutrosophic sets. Neutrosophic Sets Syst 5:15–20
Zhang HY, Wang JQ, Chen XH (2014) Interval neutrosophic sets and their application in multicriteria decision making problems. Sci World J 2014:645953
Liu P, Shi L (2014) The generalized hybrid weighted average operator based on interval neutrosophic hesitant set and its application to multiple attribute decision making. Neural Comput Appl. doi:10.1007/s00521-014-1736-4
Broumi S, Smarandache F (2014) Single valued neutrosophic trapezoid linguistic aggregation operators based multi-attribute decision making. Bull Pure Appl Sci Math Stat 33e(2):135–155
Broumi S, Ye J, Smarandache F (2014) An extended TOPSIS method for multiple attribute decision making based on interval neutrosophic uncertain linguistic variables. Neutrosophic Sets Syst 7:1–11
Tian Z-P, Wang J, Zhang H-Y, Chen X-H, Wang J-Q (2015) Simplified neutrosophic linguistic normalized weighted Bonferroni mean operator and its application to multi-criteria decision-making problems. Filomat. doi:10.2298/FIL1508576F
Wang JQ, Li XE (2015) An application of the TODIM method with multi-valued neutrosophic set. Control Decis. doi:10.13195/j.kzyjc.2014.0467
Peng J-J, Wang J-Q, Wu X-H, Wang J, Chen X-H (2015) Multi-valued neutrosophic sets and power aggregation operators with their applications in multi-criteria group decision-making problems. Int J Comput Intell Syst 8(2):345–363
Cağman N, Deli İ (2012) Products of FP-soft sets and their applications. Hacet J Math Stat 41(3):365–374
Cağman N, Deli İ (2012) Means of FP-soft sets and their applications. Hacet J Math Stat 41(5):615–625
Deli İ, Cağman N (2015) Intuitionistic fuzzy parameterized soft set theory and its decision making. Appl Soft Comput 28:109–113
Deli İ, Broumi S (2015) Neutrosophic soft matrices and NSM-decision making. J Intell Fuzzy Syst. doi:10.3233/IFS-141505
Deli İ, Broumi S (2015) Neutrosophic soft relations and some properties. Ann Fuzzy Math Inf 9(1):169–182
Broumi S (2013) Generalized neutrosophic soft set. Int J Comput Sci Eng Inf Technol 3(2):17–30
Broumi S, Deli İ, Smarandache F (2014) Relations on interval valued neutrosophic soft sets. J New Results Sci 5:1–10
Broumi S, Şahin R, Smarandache F (2014) Generalized interval neutrosophic soft set and its decision making problem. J New Results Sci 7:9–47
Broumi S, Smarandache F (2014) Lower and upper soft interval valued neutrosophic rough approximations of an IVNSS-relation. SISOM Acoust 1:204–211
Broumi S, Smarandache F (2015) Interval-valued neutrosophic soft rough sets. Int J Comput Math 2015:1–13
Roy B (1991) The outranking approach and the foundations of ELECTRE methods. Theor Decis 31:49–73
Peng J-J, Wang J-Q, Zhang H-Y, Chen X-H (2014) An outranking approach for multi-criteria decision-making problems with simplified neutrosophic sets. Appl Soft Comput 25:336–346
Orner JL, Kirkwood CW (1991) Decision analysis applications in the operations research literature 1970–1989. Oper Res 39:206–219
Haurant P, Oberti P, Muselli M (2011) Multicriteria selection aiding related to photovoltaic plants on farming fields on Corsica island: a real case study using the ELECTRE outranking framework. Energy Policy 39(2):676–688
Figueira JR, Almeida-Dias J, Matias S, Roy B, Carvalho MJ, Plancha CE (2011) Electre Tri-C, a multiple criteria decision aiding sorting model applied to assisted reproduction. Int J Med Inf 80(4):262–273
Pasiouras F, Tanna S, Zopounidis C (2007) The identification of acquisition targets in the EU banking industry: an application of multicriteria approaches. Int Rev Financ Anal 16(3):262–281
Cavallaro F (2010) A comparative assessment of thin-film photovoltaic production processes using the ELECTRE III method. Energy Policy 38(1):463–474
Montazer GA, Saremi HQ, Ramezani M (2009) Design a new mixed expert decision aiding system using fuzzy ELECTRE III method for vendor selection. Expert Syst Appl 36(8):10837–10847
Abedi M, Torabi SA, Norouzi G-H, Hamzeh M (2012) ELECTRE III: a knowledge-driven method for integration of geophysical data with geological and geochemical data in mineral prospectivity mapping. J Appl Geophys 87:9–18
Roy B (1977) Partial preference analysis and decision-aid: the fuzzy outranking relation concept. In: Bell DE, Keeney RL, Raiffa H (eds) Conflicting objectives and decisions. Wiley, New York, pp 40–75
Figueira JR, Greco S, Ehrgott M (2005) Multiple criteria decision analysis: state of the art surveys. Kluwer, Boston
Almeida-Dias J, Figueira JR, Roy B (2010) ELECTRE TRI-C: a multiple criteria sorting method based on characteristic reference actions. Eur J Oper Res 204(3):565–580
Chen T-Y (2014) An ELECTRE-based outranking method for multiple criteria group decision making using interval type-2 fuzzy sets. Inf Sci 263:1–21
Xu J, Shen F (2014) A new outranking choice method for group decision making under Atanassov’s interval-valued intuitionistic fuzzy environment. Knowl Based Syst 70:177–188
Wang JQ, Wang DD, Zhang HY, Chen XH (2013) Multi-criteria outranking approach with hesitant fuzzy sets. OR Spectr 36(4):1001–1019
Peng J, Wnag J, Wang J, Yang L, Chen X (2015) An extension of ELECTRE to Multi-criteria decision-making problems with multi-hesitant fuzzy sets. Inf Sci 307:113–126
Wang J-Q, Wang J, Chen Q-H, Zhang H-Y, Chen X-H (2014) An outranking approach for multi-criteria decision-making with hesitant fuzzy linguistic term sets. Inf Sci 280:338–351
Yang W-E, Wang J-Q (2013) Multi-criteria semantic dominance: a linguistic decision aiding technique based on incomplete preference information. Eur J Oper Res 231(1):171–181
Roy B (1982) Ranking of suburban line extension projects on the Paris metro system by a multicriteria method. Transp Res Part A Gen 16:301–312
Roy B, Vincke P (1984) Relational systems of preference with one or more pseudo-criteria: some new concepts and results. Manag Sci 30(11):1323–1335
Figueira JR, Greco S, Roy B, Słowiński R (2010) ELECTRE methods: main features and recent developments. In: Zopounidis C, Pardalos P (eds) Handbook of multicriteria analysis. Springer, Berlin, pp 51–89
Tzeng GH, Huang JJ (2011) Multiple attribute decision making: methods and applications. Chapman and Hall, London
Ye J (2012) Multicriteria decision-making method using the Dice similarity measure based on the reduct intuitionistic fuzzy sets of interval-valued intuitionistic fuzzy sets. Appl Math Model 36(9):4466–4472
Hu J, Zhang Y, Chen X, Liu Y (2013) Multi-criteria decision making method based on possibility degree of interval type-2 fuzzy number. Knowl Based Syst 43:21–29
Ye J (2014) Similarity measures between interval neutrosophic sets and their applications in multicriteria decision-making. J Intell Fuzzy Syst 26:165–172
Ye J (2013) Multicriteria decision-making method using the correlation coefficient under single-valued neutrosophic environment. Int J Gen Syst 42(4):386–394
Acknowledgments
This work was partly supported by Humanities and Social Sciences Foundation of Ministry of Education of China (No. 11YJCZH227) and the National Natural Science Foundation of China (Nos. 71221061 and 71210003). The authors also would like to express appreciation to the anonymous reviewers and editors for their helpful comments that improved the paper.
Conflict of interest
None.
Ethical standard
All the authors have read and have abided by the statement of ethical standards for manuscripts.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhang, H., Wang, J. & Chen, X. An outranking approach for multi-criteria decision-making problems with interval-valued neutrosophic sets. Neural Comput & Applic 27, 615–627 (2016). https://doi.org/10.1007/s00521-015-1882-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-015-1882-3