Skip to main content

Advertisement

Springer Nature Link
Log in

Comparison of four different heuristic optimization algorithms for the inverse kinematics solution of a real 4-DOF serial robot manipulator

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

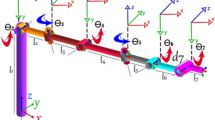
In this study, a 4-degree-of-freedom (DOF) serial robot manipulator was designed and developed for the pick-and-place operation of a flexible manufacturing system. The solution of the inverse kinematics equation, one of the most important parts of the control process of the manipulator, was obtained by using four different optimization algorithms: the genetic algorithm (GA), the particle swarm optimization (PSO) algorithm, the quantum particle swarm optimization (QPSO) algorithm and the gravitational search algorithm (GSA). These algorithms were tested with two different scenarios for the motion of the manipulator’s end-effector. One hundred randomly selected workspace points were defined for the first scenario, while a spline trajectory, also composed of one hundred workspace points, was used for the second. The optimization algorithms were used for solving of the inverse kinematics of the manipulator in order to successfully move the end-effector to these workspace points. The four algorithms were compared according to the execution time, the end-effector position error and the required number of generations. The results showed that the QPSO could be effectively used for the inverse kinematics solution of the developed manipulator.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Koker R, Oz C, Cakar T, Ekiz H (2004) A study of neural network based inverse kinematics solution for a three-joint robot. Rob Auton Syst 49:227–234

    Article  Google Scholar 

  2. Bingul Z, Ertunc HM, Oysu C (2005) Comparison of inverse kinematics solutions using neural network for 6R robot manipulator with offset. ICSC congress on computational intelligence methods and applications. Istanbul, Turkey, pp 1–5

    Google Scholar 

  3. Huang HC, Chen CP, Wang PR (2012) Particle swarm optimization for solving the inverse kinematics of 7-DOF robotic manipulators. IEEE international conference on systems, man, and cybernetics. Seoul, Korea, pp 3105–3110

    Google Scholar 

  4. Rubio JJ, Bravo AG, Pacheco J, Aguilar C (2014) Passivity analysis and modeling of robotic arms. IEEE Lat Am Trans 12(8):1381–1389

    Article  Google Scholar 

  5. Kou YL, Lin TP, Wu CY (2014) Experimental and numerical study on the semi-closed loop control of a planar robot manipulator. Math Probl Eng 2014:1–9. doi:10.1155/2014/769038

    Article  MathSciNet  Google Scholar 

  6. Kucuk S, Bingul Z (2004) The inverse kinematics solutions of industrial robot manipulators. In: IEEE international conference on mechatronics, pp 274–279

  7. Gan JQ, Oyama E, Rosales EM, Hu H (2005) A complete analytical solution to the inverse kinematics of the pioneer 2 robotic arm. Robotica 23:123–129

    Article  Google Scholar 

  8. Wang P, Li D, Zhang D, Liu K, Ni X (2007) Practical algorithm for solving real time inverse kinematics of industrial 7R robot. In: IEEE international conference on automation and logistics, pp 1963–1967

  9. Xie J, Qiang W, Liang B, Li C (2007) Inverse kinematics problem for 6‐DOF space manipulator based on the theory of screw. In: International conference on robotics and biomimetics, pp 1659–1663

  10. Sariyildiz E, Temeltas H (2009) Solution of inverse kinematics problem for serial robot using dual quaterninons and Plucker coordinates. In: IEEE/ASME international conference on advanced intelligent mechatronics, pp 338–343

  11. Karpinska J, Tchon K, Janiak M (2012) Approximation of Jacobian inverse kinematics algorithms: differential geometric vs. variational approach. J Intell Robot Syst 68:211–224

    Article  MATH  Google Scholar 

  12. Rubio JJ, Aquino V, Figueroa M (2013) Inverse kinematics of a mobile robot. Neural Comput Appl 23(1):187–194

    Article  Google Scholar 

  13. Kucuk S, Bingul Z (2014) Inverse kinematics solutions for industrial robot manipulators with offset wrists. Appl Math Model 38:1983–1999

    Article  MathSciNet  Google Scholar 

  14. Veslin EY, Dutra MS, Lengerke O, Carreño EA (2014) A hybrid solution for the inverse kinematic on a seven DOF robotic manipulator. IEEE Lat Am Trans 12(2):212–218

    Article  Google Scholar 

  15. Holland JH (1992) Genetic algorithms. Sci Am 267:66–72

    Article  Google Scholar 

  16. Kennedy J, Eberhart R (1995) Particle swarm optimization. In: IEEE international conference on neural networks, pp 1943–1948

  17. Storn R, Price K (1997) Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J Global Optim 11:341–359

    Article  MathSciNet  MATH  Google Scholar 

  18. Geem ZW, Kim JH, Loganathan GV (2001) A new heuristic optimization algorithm: harmony search. Simulation 76(2):60–68

    Article  Google Scholar 

  19. Aarts EHL, Laarhoven PJM (1989) Simulated annealing: an introduction. Stat Neerl 43:31–52

    Article  MathSciNet  MATH  Google Scholar 

  20. Dorigo M, Birattari M, Stutzle T (2006) Ant colony optimization. IEEE Comput Intell Mag 1:28–39

    Article  Google Scholar 

  21. Simon D (2008) Biogeography-based optimization. IEEE Trans Evol Comput 12:702–713

    Article  Google Scholar 

  22. Mirjalili S, Mirjalili SM, Lewis A (2014) Let a biogeography-based optimizer train your multi-layer perceptron. Inf Sci 269:188–209. doi:10.1016/j.ins.2014.01.038

    Article  MathSciNet  Google Scholar 

  23. Saremi S, Mirjalili S, Lewis A (2014) Biogeography-based optimisation with chaos. Neural Comput Appl 25(5):1077–1097

    Article  Google Scholar 

  24. Saremi S, Mirjalili S (2013) Integrating chaos to biogeography-based optimization algorithm. Int J Comput Commun Eng 2:655–658

    Article  Google Scholar 

  25. Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw 69:46–61

    Article  Google Scholar 

  26. Rashedi E, Nezamabadi-Pour H, Saryazdi S (2009) GSA: a gravitational search algorithm. Inf Sci 179:2232–2248

    Article  MATH  Google Scholar 

  27. Gandomi AH, Alavi AH (2012) Krill herd: a new bio-inspired optimization algorithm. Commun Nonlinear Sci Numer Simul 17:4831–4845

    Article  MathSciNet  MATH  Google Scholar 

  28. Guo L, Wang G-G, Gandomi AH, Alavi AH, Duan H (2014) A new improved krill herd algorithm for global numerical optimization. Neurocomputing 138:392–402

    Article  Google Scholar 

  29. Wang G-G, Gandomi AH, Alavi AH (2013) An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl Math Model 38(9–10):2454–2462

    MathSciNet  Google Scholar 

  30. Wang G-G, Gandomi AH, Alavi AH (2014) Stud krill herd algorithm. Neurocomputing 128:363–370

    Article  Google Scholar 

  31. Wang G-G, Guo L, Gandomi AH, Hao G-S, Wang H (2014) Chaotic krill herd algorithm. Inf Sci 274:17–34

    Article  MathSciNet  Google Scholar 

  32. Wang G, Guo L, Wang H, Duan H, Liu L, Li J (2014) Incorporating mutation scheme into krill herd algorithm for global numerical optimization. Neural Comput Appl 24:583–871

    Article  Google Scholar 

  33. Saremi S, Mirjalili SM, Mirjalili S (2014) Chaotic krill herd optimization algorithm. Procedia Technol 12(2014):180–185

    Article  Google Scholar 

  34. Chyan GS, Ponnambalam SG (2012) Obstacle avoidance control of redundant robots using variants of particle swarm optimization. Robot Cim Int Manuf 28(2):147–153

    Google Scholar 

  35. Huapeng W, Handroos H (2000) Inverse kinematics analysis of a parallel redundant manipulator by means of differential evolution. In: International conference on machine automation, pp 321–326

  36. Zi-wu R, Zhen-hua W, Li-ning S (2012) A global harmony search algorithm and its application to inverse kinematics problem for humanoid arm. Control Theor Appl 29(7):867–876

    Google Scholar 

  37. He G, Hongming G, Zhang G, Wu L (2006) Using adaptive genetic algorithm to the placement of serial robot manipulator serial robot manipulator. In: IEEE international conference on engineering of intelligent systems, pp 1–6

  38. Guan-Zheng T, Huan H, Aaron S (2007) Ant colony system algorithm for real-time globally optimal path planning of mobile robots. Acta Autom Sin 33(3):279–285

    Article  MATH  Google Scholar 

  39. Mon H, Xu L (2015) Research of biogeography particle swarm optimization for robot path planning. Neurocomputing 148:91–99

    Article  Google Scholar 

  40. Savsani P, Jhala RL, Savsani VJ (2014) Comparative study of different metaheuristics for the trajectory planning of a robotic arm. IEEE Syst J 2014:1–12. doi:10.1109/JSYST.2014.2342292

    Article  Google Scholar 

  41. Jordehi AR (2015) Enhanced leader PSO (ELPSO): a new PSO variant for solving global optimisation problems. Appl Soft Comput 26:401–417

    Article  Google Scholar 

  42. Toz M, Erdogmus P, Sahin I (2011) A new educational toolbox for solving robotic optimization problems using GA and PSO. E-J New World S Acad 6:1630–1644

    Google Scholar 

  43. Ayyildiz M, Cetinkaya K (2014) Inverse kinematics solution of a 4-DOF real serial robot manipulator using QPSO. In: The first international symposium on industrial design engineering, pp 1–5

  44. Eberhart R, Kennedy J (1999) A new optimizer using particle swarm theory. In: The sixth international symposium on micro machine and human science, pp 39–43

  45. Craig JJ (2005) Introduction to robotics mechanics and control, 3rd edn. Pearson Education, Upper Saddle River, NJ

    Google Scholar 

  46. Goldberg DE (1989) Genetic algorithms in search, optimization and machine learning. Addison-Wesley, USA

    MATH  Google Scholar 

  47. Jang JSR (1997) Neuro-fuzzy and soft computing: a computational approach to learning and machine intelligence. Chapter 7: derivative-free optimization. Prentice-Hall, USA

  48. Jamalipour M, Gharib M, Sayareh R, Khoshahval F (2013) PWR power distribution flattening using Quantum Particle Swarm intelligence. Ann Nucl Energy 56:143–150

    Article  Google Scholar 

  49. Sun J, Xu W, Feng B (2005) Adaptive parameter control for quantum-behaved particle swarm optimization on individual level. In: IEEE international conference on systems, man and cybernetics, pp 1–6

  50. Rashedi E, Nezamabadi-pour H, Saryazdi S (2009) GSA: a gravitational search algorithm. Inf Sci 179:2232–2248

    Article  MATH  Google Scholar 

  51. Kazak N (2011) Developed gravitational search algorithm, Bilecik University institute of science and technology, Master’s thesis

  52. Rubio JJ (2014) Stable and optimal controls of a proton exchange membrane fuel cell. Int J Control 87(11):2338–2347

    MATH  Google Scholar 

  53. Shen H, Park JH, Zang L, Wu Z (2014) Robust extended dissipative control for sampled-data Markov jump systems. Int J Control 87(8):1549–1564

    Article  MathSciNet  MATH  Google Scholar 

  54. Wilcoxon F (1945) Individual comparisons by ranking methods. Biom Bull 1:80–83

    Article  Google Scholar 

  55. Derrac J, García S, Molina D, Herrera F (2011) A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput 1(1):3–18

    Article  Google Scholar 

  56. García S, Molina D, Lozano M, Herrera F (2009) A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: a case study on the CEC’2005 special session on real parameter optimization. J Heuristics 15:617–644

    Article  MATH  Google Scholar 

  57. Mirjalili S, Lewis A (2013) S-shaped versus V-shaped transfer functions for binary particle swarm optimization. Swarm Evol Comput 9:1–14

    Article  Google Scholar 

Download references

Acknowledgments

The authors wish to thank the Karabük University Research Project Directorate, Project No.KBÜ-BAP-11-2-DR-001, for their financial support of this work.

Author information

Authors and Affiliations

  1. Manufacturing Engineering Department of Technology Faculty, Düzce University, Düzce, Turkey

    Mustafa Ayyıldız

  2. Industrial Design Engineering Department of Technology Faculty, Karabük University, Karabük, Turkey

    Kerim Çetinkaya

Authors
  1. Mustafa Ayyıldız
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Kerim Çetinkaya
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mustafa Ayyıldız.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ayyıldız, M., Çetinkaya, K. Comparison of four different heuristic optimization algorithms for the inverse kinematics solution of a real 4-DOF serial robot manipulator. Neural Comput & Applic 27, 825–836 (2016). https://doi.org/10.1007/s00521-015-1898-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-015-1898-8

Keywords